A vertical rod of mass m is kept on a wedge of mass M. If a horizontal force F acts on the wedge and the rod is constrained to move vertically, after releasing the rod-wedge system, (a) find their speeds when the wedge moves through a distance x. (b) What is the power delivered by the rod on the wedge aftre a time t measured from the instant of release?
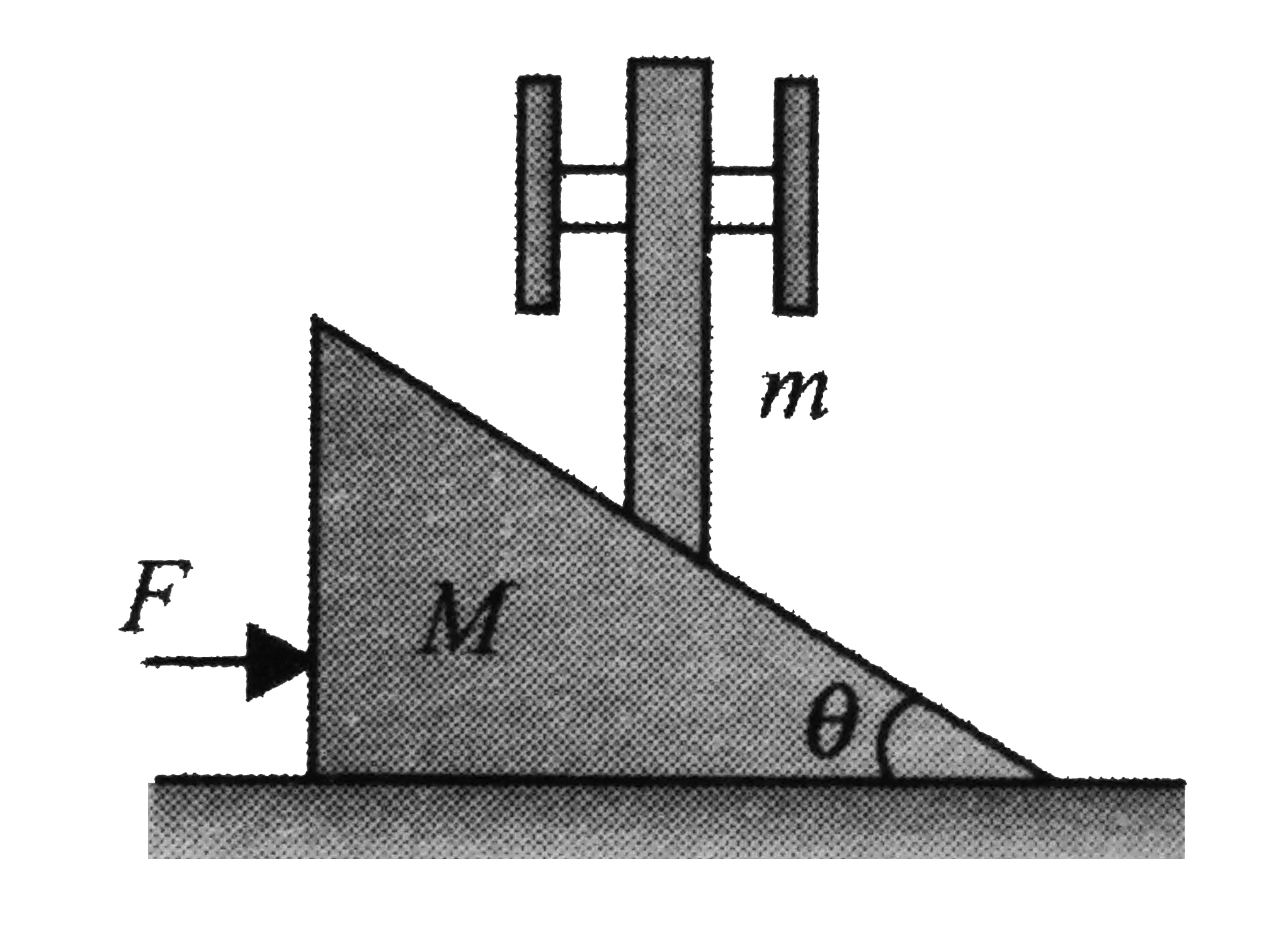
a. Let the displacement of rod is y when wedge moves a distance x,
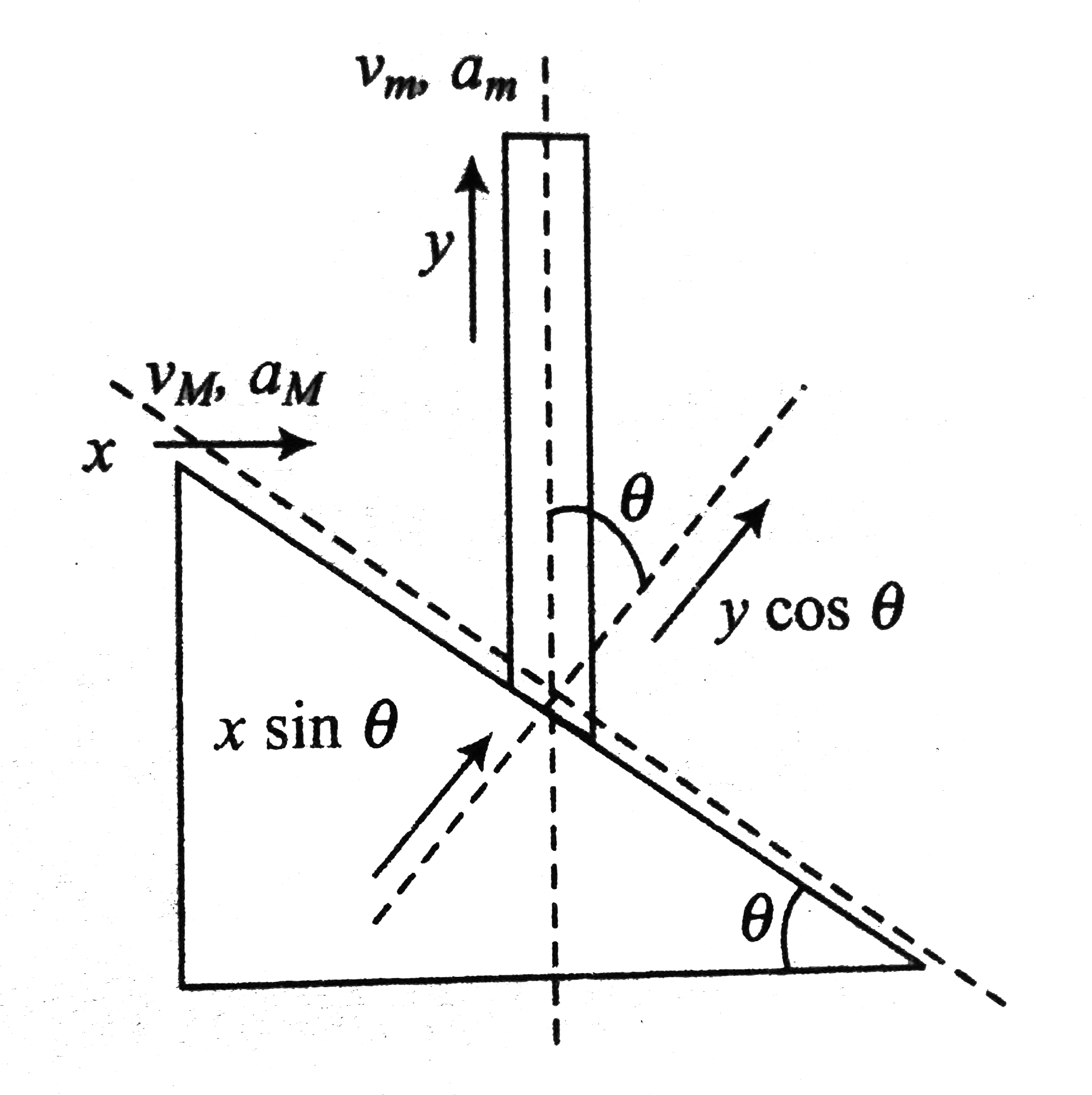
xsinθ=ycosθ⇒x=ytanθ
Also vm=vMtanθ and am=aMtanθ
Apply work-energy theorem:
W=ΔKE
⇒Fx−mgy=12Mv2M+12mv2m
⇒(F−mgtanθ)x=12Mv2M+12mv2Mtan2θ
⇒vM=√2[F−mgtanθ]xM+mtan2θ
and
vm=vMtanθ=√2[F−mgtanθ]xMcot2θ+m
b. From FBD of wedge and rod,
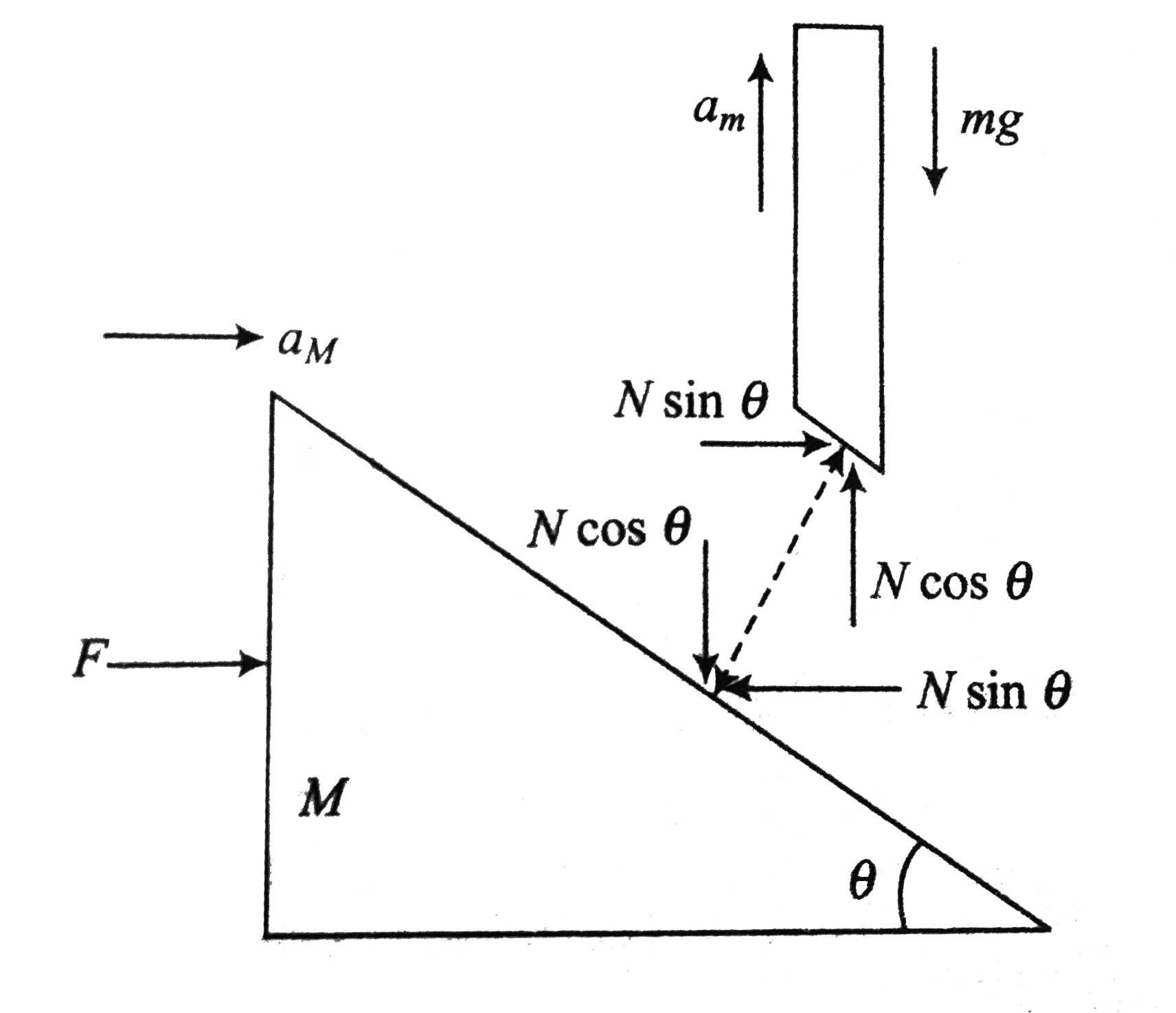
F−Nsinθ=MaM (ii)
Ncosθ−mg=mam (ii)
From (i), and (ii)
aM=F−mgtanθM+mtan2θ
N=(Ftanθ+Mg)m(M+mtan2θ)cosθ
Velocity of M after time t,
vM=aMt
Power given by rod by wedge
P=−(Nsinθ)vM
=−NaMsinθt
=−mtanθ[Ftanθ+Mg][F−mgtanθ][M+mtan2θ]2
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.2
25 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WORK, POWER & ENERGYEXERCISE - Archives (integer)
4 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
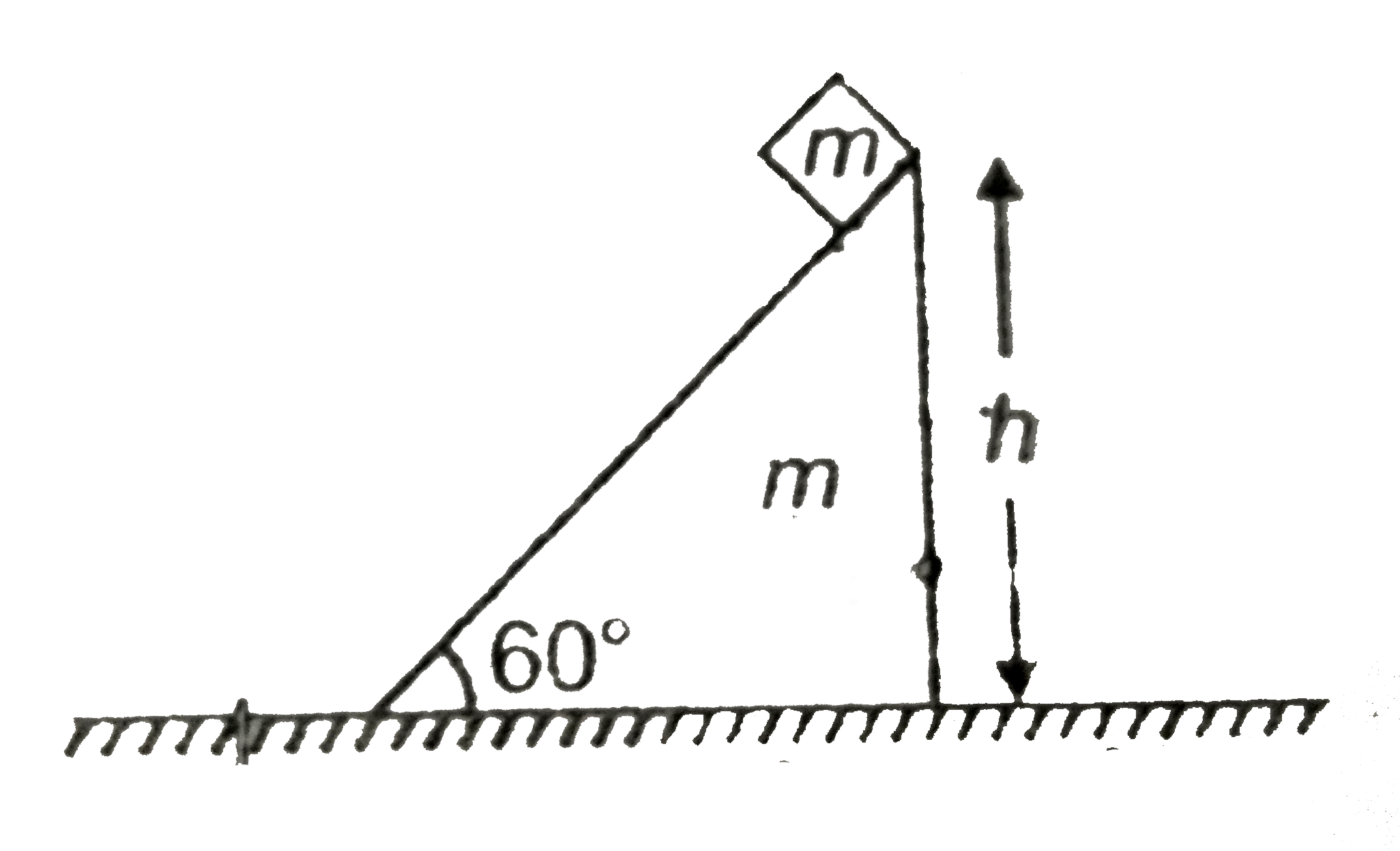
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
View SolutionA block of mass m, is kept on a wedge of mass M, as shown in figure such that mass m remains stationary w.r.t. wedge. The magnitude of force P is

View SolutionA rod of mass m is supported on a wedge of mass M shown in fig. Find the accelerations of rod and wedge in the arrangement. The friction between all contact surfaces in negligible.

View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

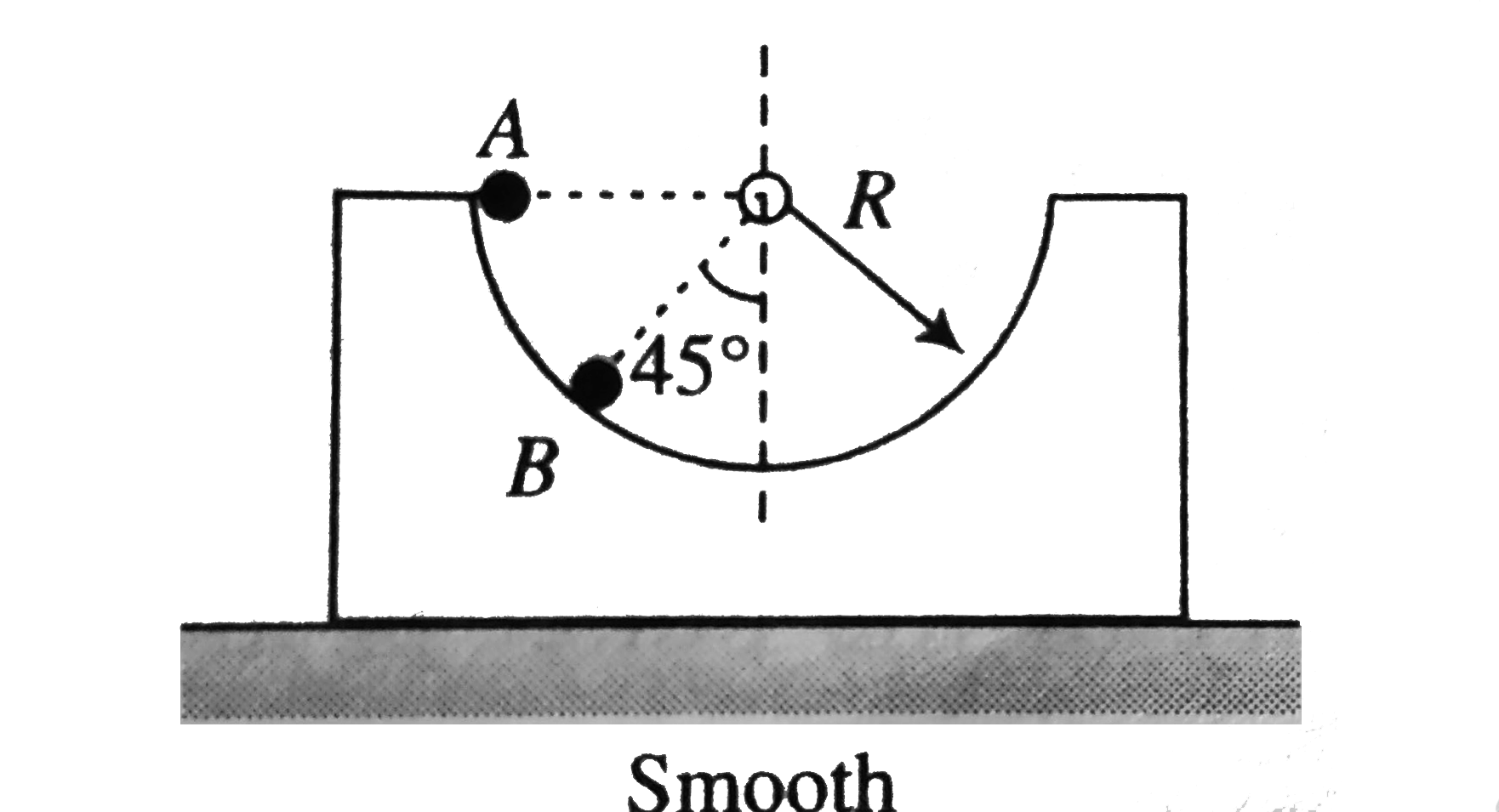
View SolutionA ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
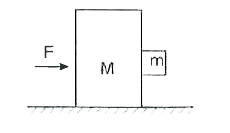
View SolutionA horizontal force F pushes wedge of mass M on a smooth horizontal surface. A block of mass m is stationary to the wedge, then:
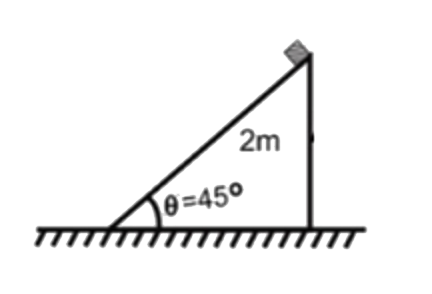
View SolutionA cube of mass m is placed on top of a wedge of mass 2m, as shown in figure. There is no friction between the cube and the wedge. The minimum co - efficient of friction between the wedge and the horizontal surface, so that the wedge does not move is
View SolutionA block of mass m is placed at the bottom of a massless smooth wedge which if placed on a horizontal surface. When we push the wedge with a constant force, the block moves up the wedge. Find the work done by the external agent when the block has a speed v and is reaches the top of the wedge.

View SolutionA block of mass m lies on wedge of mass. Mas shown in figure.

With what minimum acceleration must the wedge be moved towared right horizontally so that block m falls freely.
View Solution