A very long bar magnet is placed with its north pole coinciding with the centre of a circular loop carrying an electric current. i. The magnetic field due to the magnet at a point on the periphery of the wire is B. The radius of the loop is a. The force on the wire is
very nearly 2πaiB perpendicular to the plane of the wire.
2piaiB in the plane of the wire
πaiB along the magnet
zero
The correct Answer is:A
To solve the problem, we need to find the force acting on a circular loop carrying an electric current I when placed in the magnetic field B produced by a long bar magnet. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have a long bar magnet with its north pole at the center of a circular loop of radius a. The loop carries a current I. The magnetic field B at the periphery of the loop due to the magnet is given.
Step 2: Consider a Small Element of the Loop
Take a small segment of the loop, denoted as dl. The force dF acting on this small segment due to the magnetic field can be expressed using the formula:
dF=B⋅I⋅dl
where B is the magnetic field at the location of the segment, I is the current in the loop, and dl is the length of the small segment.
Step 3: Determine the Direction of the Force
The direction of the force can be determined using the right-hand rule. The force dF acts perpendicular to both the magnetic field B and the current I in the wire.
Step 4: Integrate Over the Entire Loop
To find the total force F on the entire loop, we need to integrate dF around the loop. Since the loop is circular, we can express the total force as:
F=∫dF=∫B⋅I⋅dl
The total length of the loop is the circumference, which is 2πa.
Step 5: Substitute and Solve
Substituting the expression for dF into the integral:
F=∫2π0B⋅I⋅dl=B⋅I⋅∫2π0dl
The integral ∫2π0dl gives the circumference of the loop, which is 2πa. Therefore, we have:
F=B⋅I⋅(2πa)
Step 6: Final Expression
Thus, the total force F acting on the wire is given by:
F=2πaIB
Summary
The force on the wire due to the magnetic field from the bar magnet is:
F=2πaIB
We have a long bar magnet with its north pole at the center of a circular loop of radius a. The loop carries a current I. The magnetic field B at the periphery of the loop due to the magnet is given.
Take a small segment of the loop, denoted as dl. The force dF acting on this small segment due to the magnetic field can be expressed using the formula:
dF=B⋅I⋅dl
where B is the magnetic field at the location of the segment, I is the current in the loop, and dl is the length of the small segment.
The direction of the force can be determined using the right-hand rule. The force dF acts perpendicular to both the magnetic field B and the current I in the wire.
To find the total force F on the entire loop, we need to integrate dF around the loop. Since the loop is circular, we can express the total force as:
F=∫dF=∫B⋅I⋅dl
The total length of the loop is the circumference, which is 2πa.
Substituting the expression for dF into the integral:
F=∫2π0B⋅I⋅dl=B⋅I⋅∫2π0dl
The integral ∫2π0dl gives the circumference of the loop, which is 2πa. Therefore, we have:
F=B⋅I⋅(2πa)
Thus, the total force F acting on the wire is given by:
F=2πaIB
The force on the wire due to the magnetic field from the bar magnet is:
F=2πaIB
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - PERMANENT MAGNETSEXERCISE - Objective II1videos
PERMANENT MAGNETS
- BOOK - HC VERMA ENGLISHCHAPTER - PERMANENT MAGNETSEXERCISE - Exercise25videos
PERMANENT MAGNETS
- BOOK - HC VERMA ENGLISHCHAPTER - PERMANENT MAGNETSEXERCISE - Worker out examples19videos
PERMANENT MAGNETS
- BOOK - HC VERMA ENGLISHCHAPTER - OPTICAL INSTRUMENTSEXERCISE - Question for short Answer12videos
OPTICAL INSTRUMENTS
- BOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - question for short answer13videos
PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITY
Similar Questions
Knowledge Check
- Question 1 - Select One
Magnetic field at the centre of a circualr loop of area A carrying current I is B. What is the magnetic moment of this loop?
A(BA)2μ0πBBA√Aμ0CBA√Aμ0πD2BA√Aμ0√π
Magnetic field at the centre of a circualr loop of area A carrying current I is B. What is the magnetic moment of this loop?
View SolutionA circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
View SolutionThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
 View Solution
View SolutionIn figure is shown a circular loop carrying current I. Show the direction of the magnetic field with the help of lines of force.
 View Solution
View SolutionA triangular loop of side l carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
View SolutionFind the magnetic force on loop PQRS due to the wire.
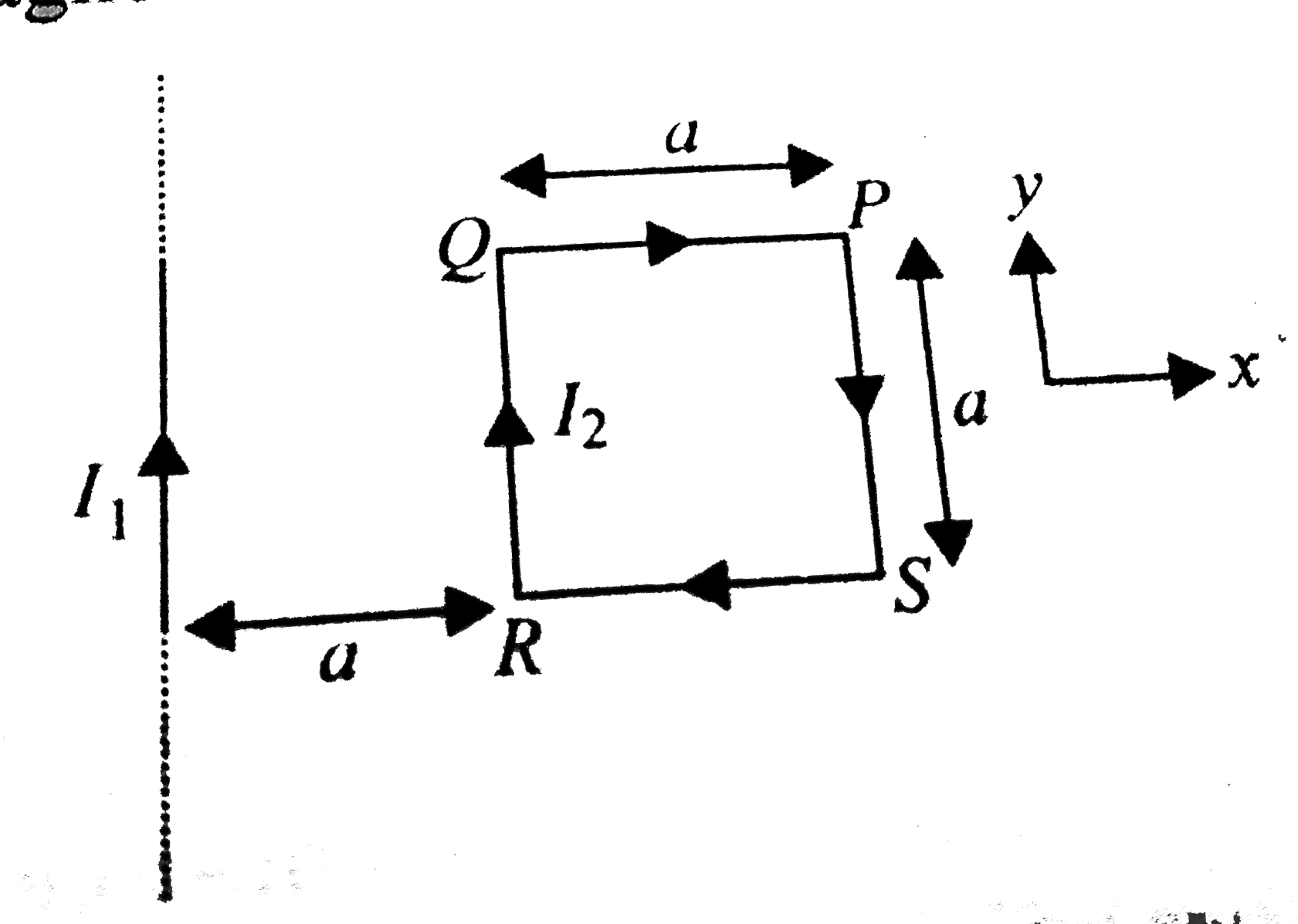 View Solution
View Solution

