A water barrel stands on a table of height h. If a small holes is punched in the side of the barrel at its base, it is found that the resultant stream of water strikes the ground at a horizontal distance R from the table. What is the depth of water in the barrel?
R2h
R22h
R24h
4R2h
The correct Answer is:C
To find the depth of water in the barrel when a small hole is punched in the side at the base, we can follow these steps:
1. Identify Variables:
- Let H be the depth of water in the barrel.
- Let h be the height of the table.
- Let R be the horizontal distance from the table where the water strikes the ground.
2. Determine the Velocity of Water:
- According to Torricelli's theorem, the velocity V of water flowing out of the hole at the base of the barrel is given by:
V=√2gH
where g is the acceleration due to gravity.
3. Calculate the Time of Flight:
- The water falls a vertical distance of h (the height of the table). The time t taken to fall this distance can be calculated using the equation of motion:
h=12gt2
Rearranging gives:
t=√2hg
4. Calculate the Horizontal Range:
- The horizontal range R can be expressed as:
R=V⋅t
Substituting the expressions for V and t:
R=√2gH⋅√2hg=√4hH
5. Square Both Sides:
- Squaring both sides of the equation gives:
R2=4hH
6. Solve for Depth H:
- Rearranging the equation to find H:
H=R24h
Final Answer:
The depth of water in the barrel is:
H=R24h
- Let H be the depth of water in the barrel.
- Let h be the height of the table.
- Let R be the horizontal distance from the table where the water strikes the ground.
- According to Torricelli's theorem, the velocity V of water flowing out of the hole at the base of the barrel is given by:
V=√2gH
where g is the acceleration due to gravity.
- The water falls a vertical distance of h (the height of the table). The time t taken to fall this distance can be calculated using the equation of motion:
h=12gt2
Rearranging gives:
t=√2hg
- The horizontal range R can be expressed as:
R=V⋅t
Substituting the expressions for V and t:
R=√2gH⋅√2hg=√4hH
- Squaring both sides of the equation gives:
R2=4hH
- Rearranging the equation to find H:
H=R24h
The depth of water in the barrel is:
H=R24h
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Higher Order Thinking Skills8videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Exemplar Problems5videos
MECHANICAL PROPERTIES OF FLUIDS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason15videos
LAWS OF MOTION
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assertion And Reason15videos
MECHANICAL PROPERTIES OF SOLIDS
Similar Questions
A tank of height H is fully filled with water. If the water rushing from a hole made in the tank below the free surface , strikes the floor at a maximum horizontal distance , then the depth of the hole from the free surface must be
View SolutionA tank is filled by water (ρ=103kg/m3). A small hole is made in the side wall of the tank at depth 10 m below water surface. A water jet emerges horizontal from the hole and falls at horizontal distance R from it. The amount of extra pressure (in terms of atmospheric pressure) that must be applied on the water surface, so that range becomes 3R on the on the ground will be (cross section area of hole is negligible and 1 atm = 105 Pa, g = 10 m/s2)
View SolutionWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
View SolutionA stone is thrown horizontally with a velocity 2√gh from the top of a tower of height h. It strikes the ground level through the foot of tower at a distance x from it. What is the value of x?
View SolutionA tank is filled with water upto a height H. A hole is punched in one of the walls at a depth h1 below the water surface. (a) Find the distance from the foot of the wall at which the stream strikes the floor. (6) Is it possible to make second hole at another depth so that this second stream also has the same range? If so find its depth ?
View SolutionA tank if filled with water upto height H. When a hole is made at a distance h below the level of water. What will be the horizontal range of water jet ?
View Solution_E01_261_Q01.png)
Consider a water jar of radius R that has water filled up to height H and is kept on a stand of height h (see figure) through a hole of radius r(r<<R) at its bottom the water leaks out and the stream of water coming down towards the gound has a shape like a funnel as shown in the figure. it the radius of teh cross-section of water stream when it hits the ground is x. then.View SolutionA liquid is filled in a container to a height H. A small hole is opened in the side of the container a height h below the surface of the liquid. The distance L from the bottom of the container of the point where the stream of liquid leaving the container meets the ground is :
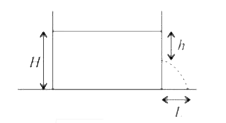 View Solution
View Solution_S01_054_Q01.png)
An open vessel full of water is falling freely under gravity. There is a small hole in one face of the vessel, was shown in te figure. The water which comes out from the hole at the instant when hole is at height H above the ground strikes the ground at a distance of x from P. Which of the followin is correct for the situation described?
(a). The value of x is 2√2hH3
(b). The value of x is √4hH3
(c). The value ofx can't be computed from information providec.
(d). The question is irrevalent as no water comes out from the hole.View SolutionA ball is thrown from a point in level with velocity u and at a horizontal distance r from the top os a tower of height h.
At what horizontal distance x from the foot of the tower does the ball hit the ground ? View Solution
View Solution

