A weight of mass m=1 kg attached to a spring of force constant k=20Nm−1 is able to oscillate on a rouch (μ=0.05) steel rod. The displacement from the initial position of equilibrium is a=30 cm. Find how many swings (i.e., movement from maximum to the equilibrium or back) will it make before coming to rest ? Take g=10ms−2
[Hint : Use energy conservation to find an and hence have number of swings]
The correct Answer is:N=kaμmg−1=11
Step by step video, text & image solution for A weight of mass m=1 kg attached to a spring of force constant k = 20 N m"^(-1) is able to oscillate on a rouch (mu = 0.05) steel rod. The displacement from the initial position of equilibrium is a=30 cm. Find how many swings (i.e., movement from maximum to the equilibrium or back) will it make before coming to rest ? Take g = 10 ms^(-2) [Hint : Use energy conservation to find a_(n) and hence have number of swings] by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FRICTION, WORK POWER AND ENERGYBOOK - NN GHOSHCHAPTER - FRICTION, WORK POWER AND ENERGYEXERCISE - Exercises (A)
15 Videos
- FIRST LAW OF THERMODYNAMICSBOOK - NN GHOSHCHAPTER - FIRST LAW OF THERMODYNAMICSEXERCISE - All Questions
39 Videos
- GRAVITATIONBOOK - NN GHOSHCHAPTER - GRAVITATIONEXERCISE - EXERCISE
29 Videos
Similar Questions
A weight of mass 1 kg attached to a spring with a force constant of 20 N/m is able to oscillate on a horizontal
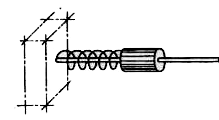
steel rod Fig. The initial displacement from the position of equilibrium is 30 cm. Find how many swings the weight will make before stopping completely. One swing is the movement from maximum displacement to the equilibrium position (or back). For numerical calculation put g=10m/s2 and coefficient of friction μ=0.05.
View SolutionA block of mass 0.2 kg is attached to a mass less spring of force constant 80 N/m as shown in figure. Find the period of oscillation. Take g=10m/s2. Neglect friction

View Solution
Knowledge Check
A 5 kg collar is attached to a spring of spring constant 500 N m−1. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. The time period of oscillation is
Aπ5sBπ2sCπsD2πsa block of mass 0.1 kg attached to a spring of spring constant400Nm pulled horizontally from x=0 tox1=10mm. Find the work done by the spring force
A2⋅10−2JB2⋅10−6JC3⋅10−6JD4⋅10−2JA block of mass 1 kg is attached to one end of a spring of force constant k = 20 N/m. The other end of the spring is attached to a fixed rigid support. This spring block system is made to oscillate on a rough horizontal surface (μ=0.04). The initial displacement of the block from the equilibrium position is a = 30 cm. How many times the block passes from the mean position before coming to rest ? (g=10m/s2)
A11B7C6D15
A block of mass 0.1 kg attached to a spring of spring constant 400 N/m is pulled rightward from x0=0 to x1=15 mm. Find the work done by spring force.
View SolutionA 2.5 kg collar attached to a spring of foce constant 1000 Nm−1 slides without friction on a horizontal rod. The collar is displaced from its equilibrium position by 5.0 cm and released. Calculate (i) the period of oscillation (ii) the maximum speed of the collar and (iii) the maximum acceleration of the collar.
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximu speed of the trolley is
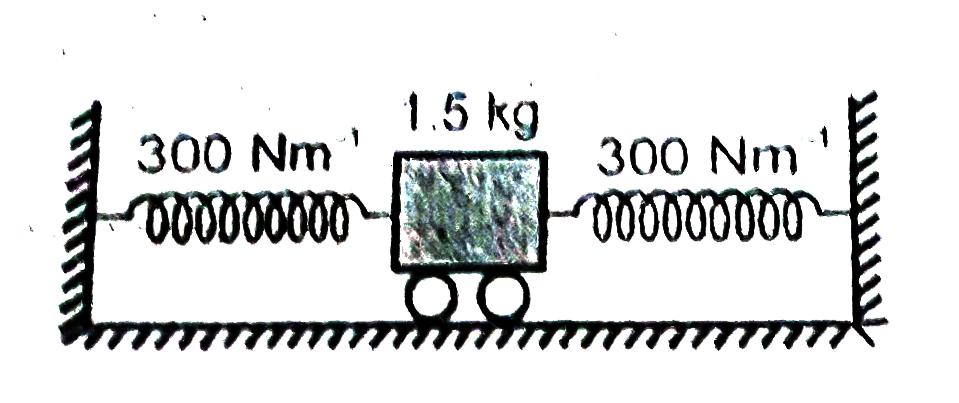
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
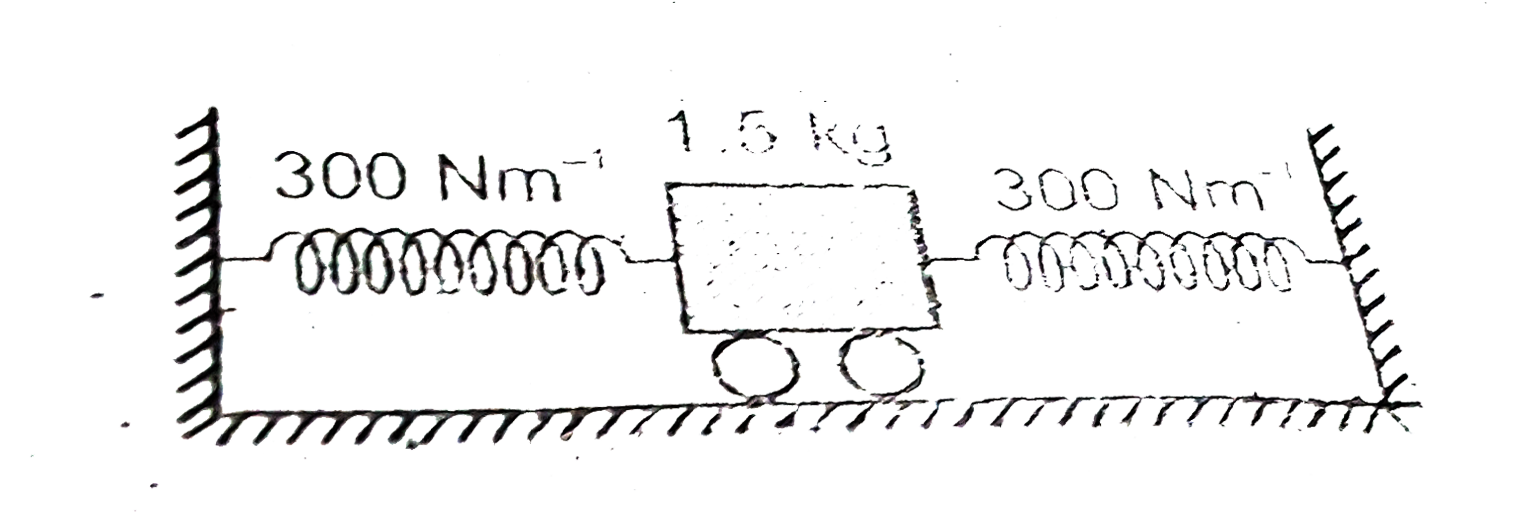
View SolutionA block of mass 2kg is connected with a spring of natural length 40cm of force constant K=200N/m. The cofficient of friction is μ=0.5. When released from the given position, acceleration of block will be

View Solution
