A wheel is mounted on frictionless central pivot and it can rotate freely in the vertical plane. There is a horizontal light rod fixed to the wheel below the pivot. There is a small sleeve of mass m which can slide along the rod without friction. The sleeve is connected to a light spring. The other end of the spring is fixed to the rim as shown. The sleeve is at the centre of the rod and the spring is relaxed. Now the wheel is held at rest and the sleeve is moved towards left so as to compress the sprig by some distance. The sleeve and the wheel are released simultaneously from this position.
(a) Is it possible that the wheel does not rotate as the sleeve perform SHM on the rod ?
(b) Find the value of spring constant k for situation described in (a) to be possible. The distance of rod from centre of the wheel is d.

The correct Answer is:(a) yes
(b) k=mgd
Step by step video, text & image solution for A wheel is mounted on frictionless central pivot and it can rotate freely in the vertical plane. There is a horizontal light rod fixed to the wheel below the pivot. There is a small sleeve of mass m which can slide along the rod without friction. The sleeve is connected to a light spring. The other end of the spring is fixed to the rim as shown. The sleeve is at the centre of the rod and the spring is relaxed. Now the wheel is held at rest and the sleeve is moved towards left so as to compress the sprig by some distance. The sleeve and the wheel are released simultaneously from this position. (a) Is it possible that the wheel does not rotate as the sleeve perform SHM on the rod ? (b) Find the value of spring constant k for situation described in (a) to be possible. The distance of rod from centre of the wheel is d. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Let →u be the initial velocity of a particle and →F be the resultant force acting on it . Describe the path that the particle can take if
(a) →u×→F=0and→F=constant
(b) →u.→F=0and→F=constant
In which case can the particle retrace its path .
View SolutionTwo particles of mass m1 and m2 are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity V0 along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass m1(orm2) will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of m1 and m2 as a function of time. lt( c) Write the X co ordinates of m1 and m2 as a function of time

View SolutionA horizontal smooth rod AB rotates with a constant angular velocity ω=2.00rad/s about a vertical axis passing through its end A. A freely sliding sleeve of mass m=0.50g moves along the rod from the point A with the initial velocity v0=1.00m/s. Find the Coriolis force acting on the sleeve (in the reference frame fixed to rotating rod) at the moment when the sleeve is located at the distance r=50cm from the rotation axis.
View SolutionA smooth uniform rod AB of mass M and length l rotates freely with an angular velocity omega_0 in a horizontal plane about a stationary vertical axis passing through its end A. A small sleeve of mass m starts sliding along the rod from the point A. Find the velocity v^' of the sleeve relative to the rod at the moment it reaches its other and B.
View SolutionIn the arrangement shown in figure the sleeve M of mass m=0.20kg is fixed between two identical springs whose combined stiffness is equal to x=20N/m. The sleeve can slide without friction over a horizontal bar AB. The arrrangement rotates with a constant angular velocity ω=4.4rad/s about a vertical axis passing through the middle of the bar . Find the period of small oscillations of the sleeve. At what values of ω will there be no oscillations of the sleeve ?
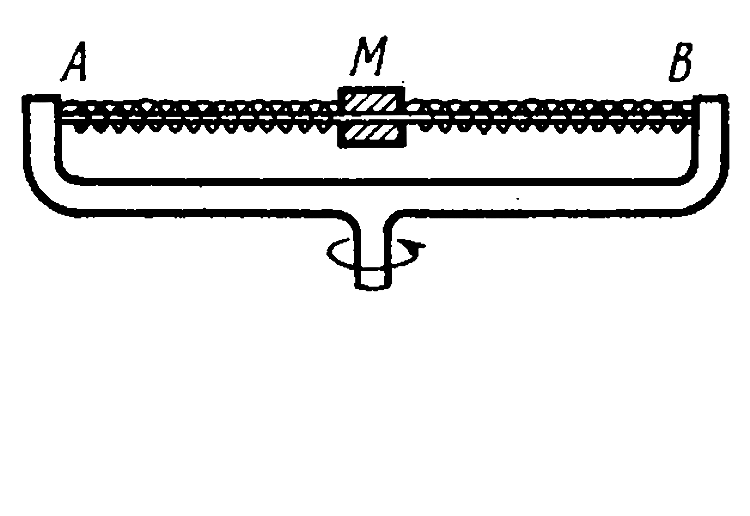
View SolutionIn the arrangement shown, the sleeve of mass M is fixed between two identical springs whose combined force constant is k . The sleeve can slide without friction over a horizontal bar AB . The arragement rotates with a constant angular velocity omega about a vertical axis passing through the middle of the bar. the period of small oscillations of teh sleeve is.........
View SolutionA rough L- shaped rod is located in a horizontal plane and a sleeve of mass m is inserted in the rod. The rod is rotated with a constant angular velocity ω in the horizontal plane. The length l1 and l2 are shown in figure. The normal reaction and frictional force acting on the sleeve when it starts slipping are
(μ: coefficient of friction between rod and sleeve)

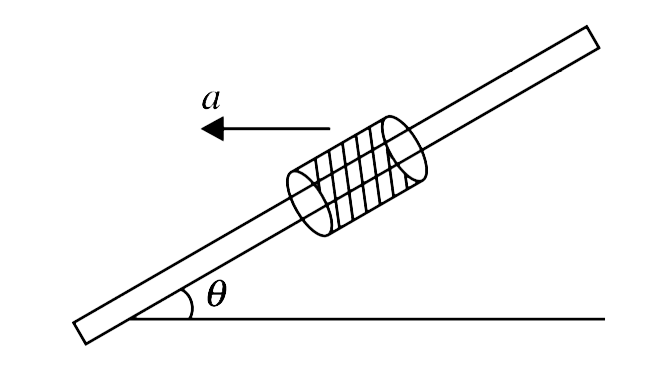
View SolutionA rod is kept inclined at an angle θ with the horizontal A sleeve of mass m can slide on the rod. If the coefficient of friction between the rod and the sleeve is μ, for what values of horizontal acceleration a of the rod, towards left, the sleeve will not slide over the rod?
View SolutionA light rod AB is fitted with a small sleeve of mass m which can slide smoothly over it. The sleeve is connected to the two ends of the rod using two springs of force constant 2k and k (see fig). The ends of the springs at A and B are fixed and the other ends (connected to sleeve) can move along with the sleeve. The natural length of spring connected to A is l0. Now the rod is rotated with angular velocity w about an axis passing through end A that is perpendicular to the rod. Take kmω2=η and express the change in length of each spring (in equilibrium position of the sleeve relative to the rod) in terms of l0 and η.

View SolutionA rod of length l=2m is maintained to rotate with a constant angular velocity omega=1 rad//s about vertical axis passing through one end (fig). There is a spring of spring constant k=1 N//m which just encloses rod inside it in natural length. One end of the spring is attached to axis of rotation. S is sleeve of mass m=1kg which can just fir on rod. All surfaces are smooth. With what minimum kinetic energy (in J ) sleeve should be projected so that it enters on the rod without impulse and completely compresses the spring.
View SolutionA small sleeve of mass m=1/10kg can move along the diameter of a horizontal disc, which slides without friction along a guide rode. The sleeve is tied to the end of the rod with the aid of a massless spring whose force constant k=10N/m. When the spring is not under tension, the sleeve is at the oscillations of the sleeve when the disc rotates about its axis at the angular speed ω equal to a) 6 rad/s, b) 15 rad/s.

View Solutiontwo light identical springs of spring constant K are attached horizontally at the two ends of a uniform horizontal rod AB of length l and mass m. the rod is pivoted at its centre 'o' and can rotate freely in horizontal plane . The other ends of the two springs are fixed to rigid supportss as shown in figure . the rod is gently pushed through a small angle and released , the frequency of resulting oscillation is :
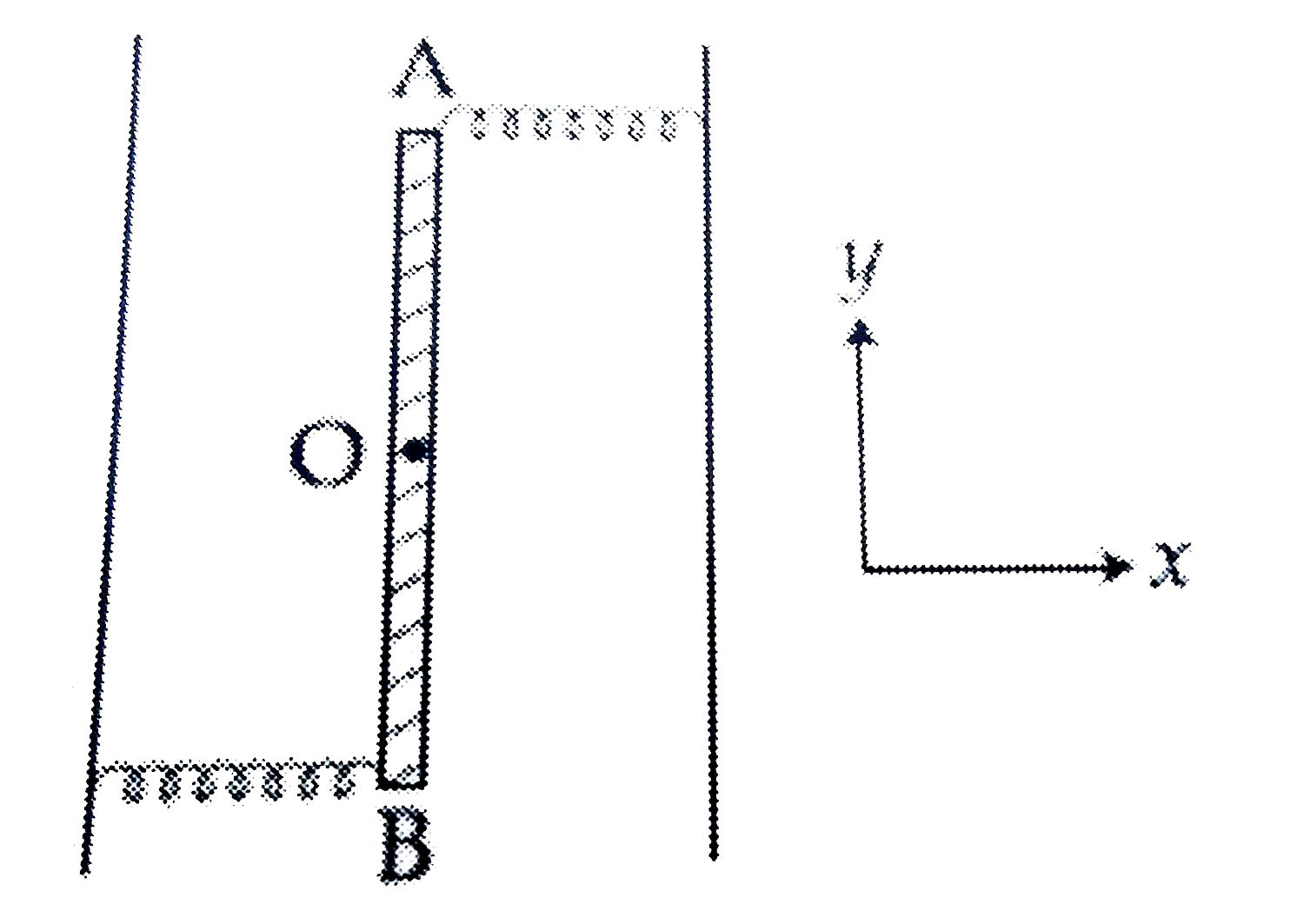
View SolutionA straight rod of light L and mass m is pivoted freely from a point of the roof. Its lower end is connected to an ideal spring of spring constant K. The other end of the spring is connected to the wall as shown in the figure. Find the frequency of small oscillation of the system.
View SolutionL shaped rod whose one end is horizontal and other is vertical is rotating about a vertical axis as shown with angular speed omega .The sleeve has mass m and friction coefficient between rod and sleeve is mu .The minimum angular speed omega for which sleeve cannot slip on rod is?
View Solutiontwo light identical springs of spring constant K are attached horizontally at the two ends of a uniform horizontal rod AB of length l and mass m. the rod is pivoted at its centre 'o' and can rotate freely in horizontal plane . The other ends of the two springs are fixed to rigid supportss as shown in figure . the rod is gently pushed through a small angle and released , the frequency of resulting oscillation is :
View Solution
