A wheel of radius R has an axle of radius R/5. A force F is applied tangentially to the wheel. To keep the system in a state of "rotational" rest, a force F' is applied tangentially to the axle. The value of F' is
F
3F
5F
7F
The correct Answer is:C
To solve the problem, we need to analyze the forces and torques acting on the wheel and the axle. Here’s a step-by-step solution:
Step 1: Understand the system
We have a wheel of radius R and an axle of radius R5. A force F is applied tangentially to the wheel, and we need to find the force F′ that is applied tangentially to the axle to keep the system in a state of rotational rest.
Step 2: Set up the torque equation
To keep the system in rotational rest, the net torque about any point must be zero. We can choose the center of the wheel (point O) as our pivot point. The torque due to the force F acting on the wheel is given by:
Torque due to F=F⋅R
The torque due to the force F′ acting on the axle is given by:
Torque due to F′=F′⋅(R5)
Step 3: Write the torque balance equation
Since the system is in rotational rest, the total torque about point O must be zero:
F⋅R−F′⋅(R5)=0
Step 4: Solve for F′
Rearranging the equation gives:
F⋅R=F′⋅(R5)
Now, we can cancel R from both sides (assuming R≠0):
F=F′⋅(15)
Multiplying both sides by 5, we find:
F′=5F
Final Answer
Thus, the value of F′ is:
F′=5F
---
We have a wheel of radius R and an axle of radius R5. A force F is applied tangentially to the wheel, and we need to find the force F′ that is applied tangentially to the axle to keep the system in a state of rotational rest.
To keep the system in rotational rest, the net torque about any point must be zero. We can choose the center of the wheel (point O) as our pivot point. The torque due to the force F acting on the wheel is given by:
Since the system is in rotational rest, the total torque about point O must be zero:
Rearranging the equation gives:
Thus, the value of F′ is:
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
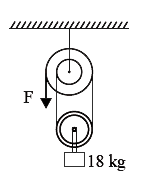
In the figure at the free end a force F is applied to keep the suspended mass of 18 kg at rest. The value of F is :
View SolutionA whel of mass 2kg an radius 10 cm is rotating about its axis at an angular velocity of 2πrad/s the force that must be applied tangentially to the wheel to stop it in 5 revolutions is
View SolutionIf force F is applied on a body and it moves with a velocity v, the power will be
View SolutionA wheel of mass 10 kg and radius 0.2 m is rotating at an angular speed of 100 rpm, when the motion is turned off. Neglecting the friction at the axis. Calculate the force that must be applied tangentially to the wheel to bring it to rest in 10 rev. Assumed wheel to be a disc.
View SolutionA wheel of mass 10 kg and radius 0.2 m is rotating at an angular speed of 100 rpm, when the motion is turned off. Neglecting the friction at the axis. Calculate the force that must be applied tangentially to the wheel to bring it to rest in 10 rev. Assumed wheel to be a disc.
View SolutionA disc of mass M kg and radius R metre is rotating at an angular speed of ω rad/s when the motor is switched off. Neglecting the friction at the axie, the force that must be applied tangentially to the wheel to bring it to rest time t is
View SolutionIn the situation given, a force F is applied at the top of sphere. Study following statements.

View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

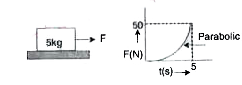
View SolutionA force F is applied to the initially stationary cart. The variation of force with time is shown in the figure. The speed of cart at t = 5 sec is
View SolutionA solid cylinder wheel of mass M and radius R is pulled by a force F applied to the centre of the wheel at 37∘ to the horizontal. If the wheel is to roll without slipping, what is the maximum value of |F| ? The coefficients of static and kinetic friction are μs=0.40 and mk=0.30.(sin37∘=35)
View Solution
