A wheel of rdius r and moment of inertia I about its axis is fixed at top of an inclined plane of inclination θ as shownin figure. A string is wrapped round the wheel and its free end supports a block of mass M which can slide on the plane. INitialy, tehwheel is rotating at a speed ω in direction such that the block slides pu the plane. How far wil the block move before stopping?

Let a be the deceleration of the block moving up the incline. Therefore, liner deceleration of the rim of the wheel would also be a.
Angular deceleration of wheel
α=ar ..(i)
It T is tension in the string, then equation of motion of block would be
Mgsinθ−T=Ma ...(i)
Also, τ=T×r=Iα
∴T=Iαr=Iar2 using (i)
Put in (ii)
Mgsinθ=Ma+T=Ma+Iar2
=a(M+Ir2)=a(Mr2+Ir2)
a=Mgr2sinθI+Mr2
Initial velocity of the block up the incline
v=rω
∴ Distance moved by the block before stopping
s=v22a=r2ω2(I+Mr2)2Mgr2sinθ
s=(I+Mr2)ω22Mgsinθ
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT
21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ADDITIONAL EXERCISES
11 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE E
1 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
Moment of inertia of a disc about its own axis is I. Its moment of inertia about a tangential axis in its plane is
View SolutionA wheel of moment of inertia I and rdius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.

View Solution
Knowledge Check
A block of mas m begins to slide down on an inclined plane of inclination θ. The force of friction will be
AmgBmgcosθCmgsinθDmgtanθA sphere of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then initally
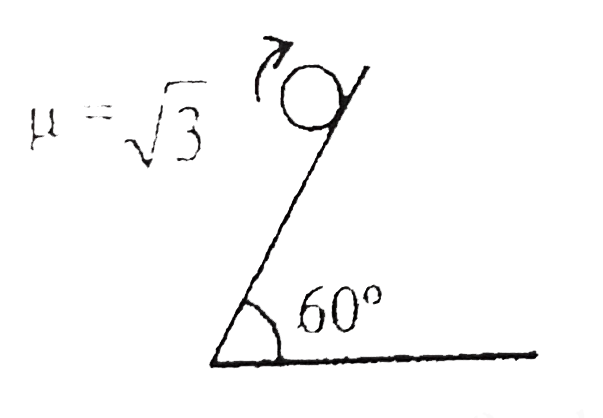 Athe centre of mass of sphere accelerates upwards.Bthe centre of mass of shpere accelerates downwardsCthe lowest point of contact accelerates upwards.Dthe lowest point of contect accelerates downwards.
Athe centre of mass of sphere accelerates upwards.Bthe centre of mass of shpere accelerates downwardsCthe lowest point of contact accelerates upwards.Dthe lowest point of contect accelerates downwards.A block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
AmgBmgsinθ√1+μ2CmgsinθD√(mgsinθ)2+(μmgcosθ)2
A block is about to slide down an inclined plane when its inclination to the horizontal is θ. If now a 5 kg weight is attached on the block :
View SolutionA wheel of mass M and radius a and M.I. IG (about centre of mass) is set rolling with angular velocity ω up a rough inclined plane of inclination theta. The distance traveled by it up the plane is
View SolutionAn cylinder of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then :
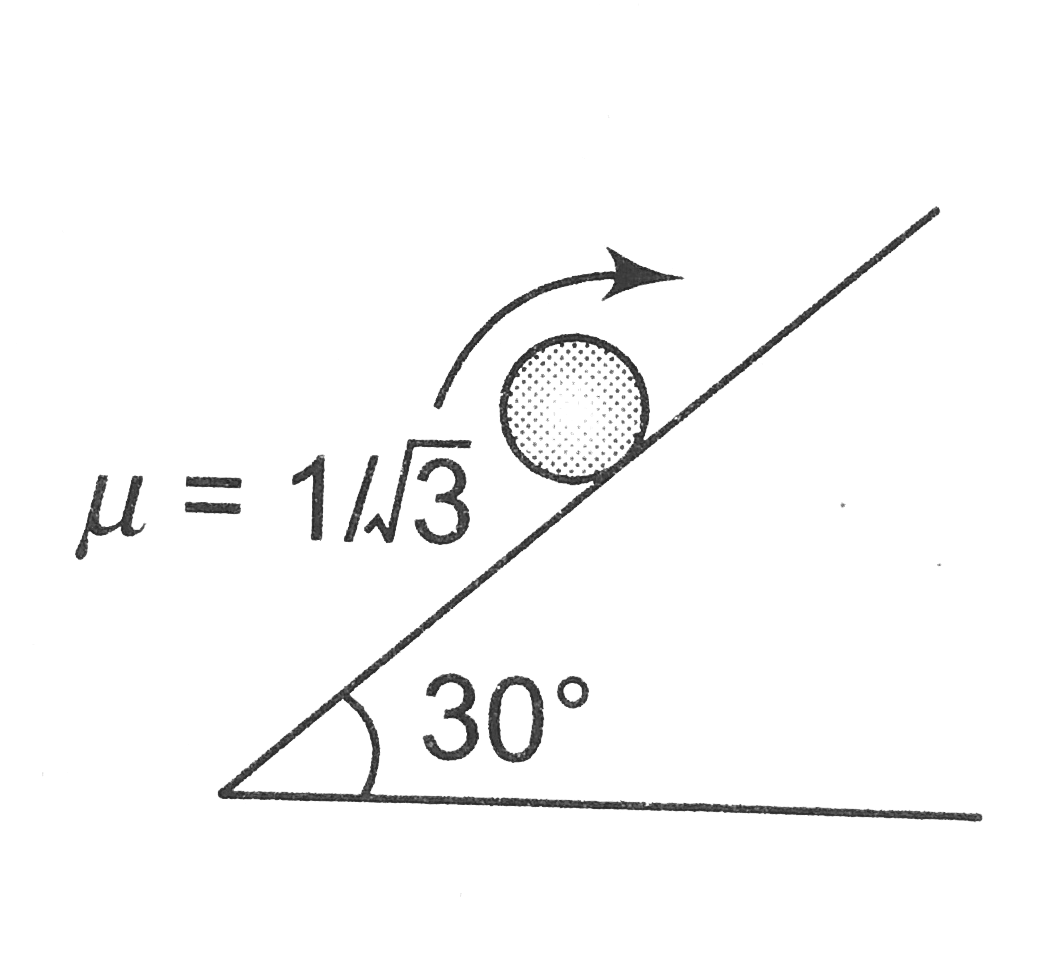 .
.
View SolutionA block of mass m is resting on an inclined plane. The inclination of the plane to the horizontal is gradually increased. It is found that when angle of inclination is θ, the block just begins to slide down the plane. What is the minimum force F applied parallel to the plane that would just make the block move up the plane?
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View Solution
