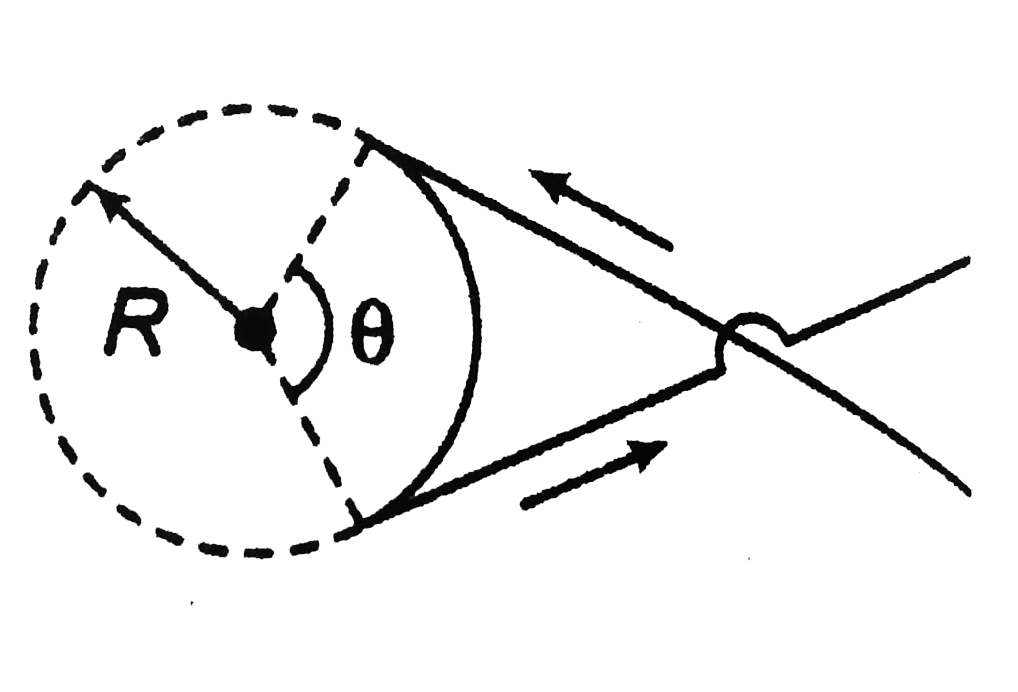
A wire carrying current i has the configuration as shown in figure. Two semi-infinite straight sections, both tangent to the same circle, are connected by a circular arc of central angle theta, along the circumference of the circle, with all sections lying in the same plane. What must be for B to be zero at the centre of the circle?
The correct Answer is:A, B, D
Two straight wires produces outward magnetic field by arc of circle produces inward magnetic field.
Due to straight wires,
B1=2[μ04πiR(sinθ+sin90I∘)]
=μ02πR(outwards)<br>Due to circle arc B2=θ2π(μ0i2R)(inward)
For net to be zero
B1=B2
orθ=2rad
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Video
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Video
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Video
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEYCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Video
Similar Questions
A conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

View SolutionThe configuration of some current carrying wires is shown in figure-4.217. All straight wires are very long. Both AB and CD are arcs of the same circle, both subtending right angles at the centre 0. The magnetic field at O is:
View Solution
Knowledge Check
A part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
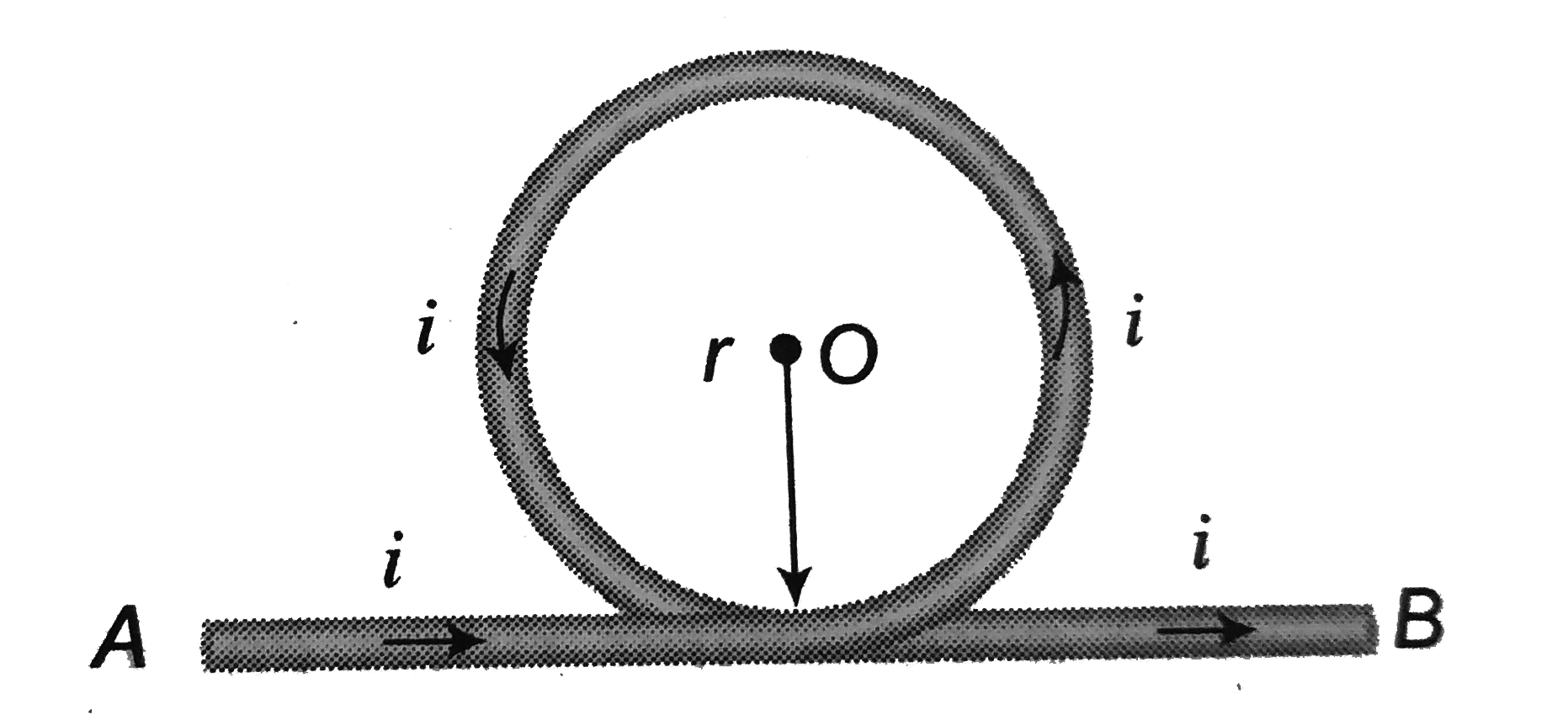 Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)
Aμ0i4rBμ0i2rCμ0i2πr(π+1)Dμ0i2πr(π−1)Two long straight wires are connected by a circular section which has a radius R. All the three segments lie in the same plane and carry a current I. The magnetic induction at the centre O of the circular segments is
 Aμ0I4πRBαμ0I4πRCαμ0IRDαμ0I2πR
Aμ0I4πRBαμ0I4πRCαμ0IRDαμ0I2πRFigure. Shows a small loop carrying a current I. The curved portion is an arc of a circle of radius R and the straight portion is a chord to the same circle subtending an angle θ. The magnetic induction at centor O is
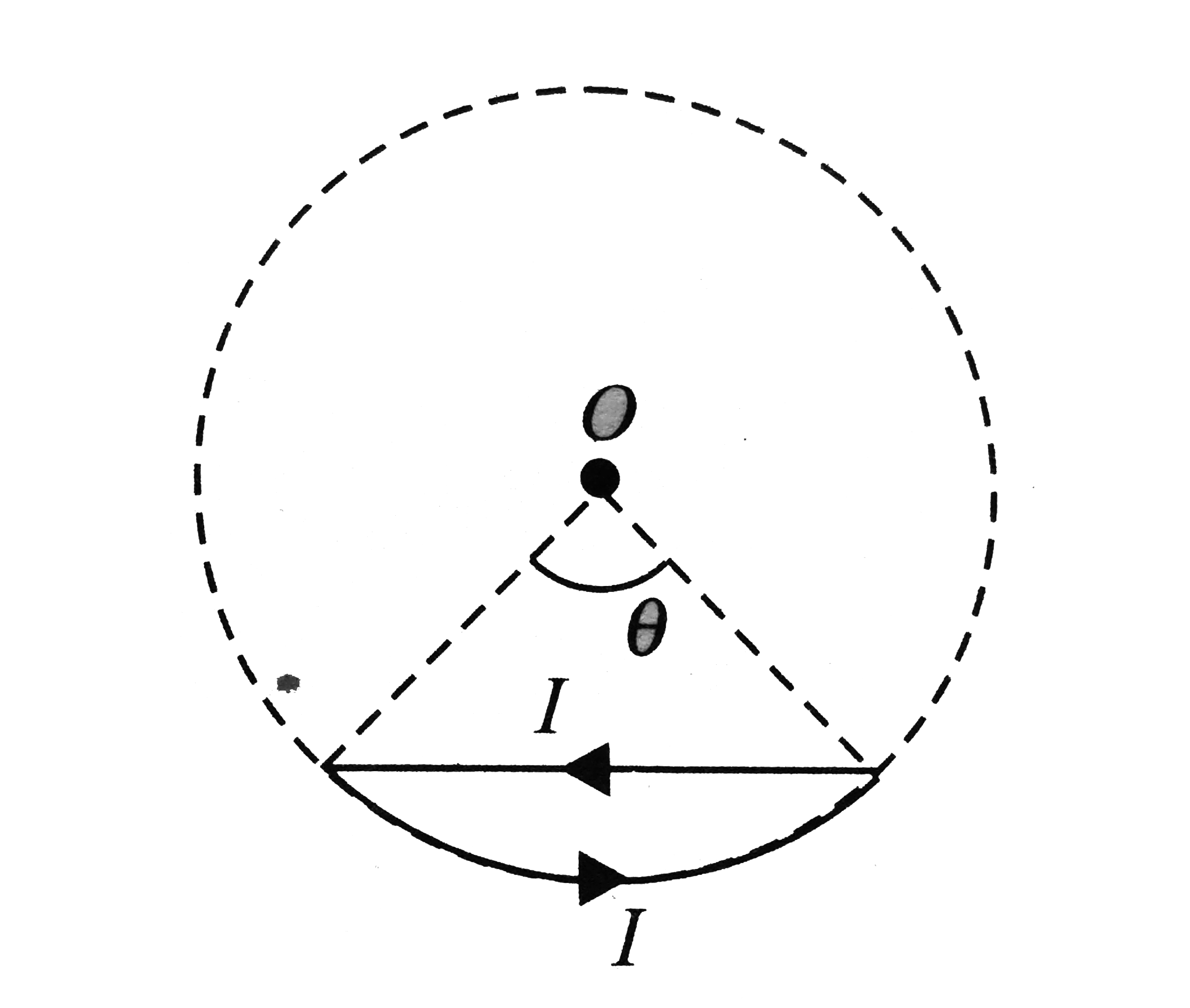 AzeroBalways inward irrespective of the value θCinward as long as θ is less than πDalways outward irrespective of the value of θ
AzeroBalways inward irrespective of the value θCinward as long as θ is less than πDalways outward irrespective of the value of θ
A current of 10A flows around a closed path in a circuit which is int eh horizontal plne as shown in the figure. The circuit consists oif eight alternating arcs of radii r1=0.08m and r2=0.12m. Each subtends the same angle at the centre.
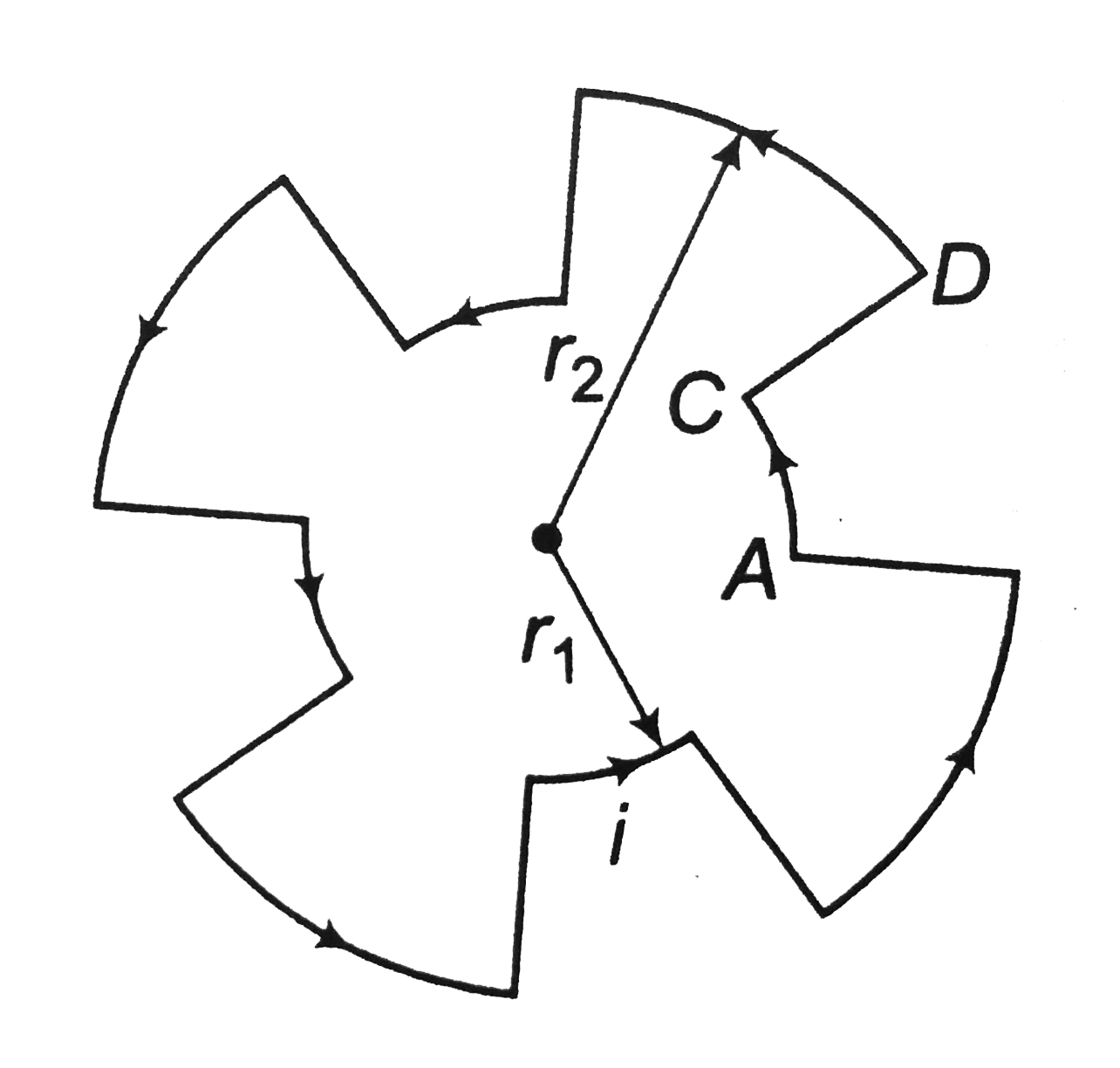
a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carryin as current of 10A is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centredue to the curren in the circuit? What is the force acting on the arc AC and the straight segment CD due to the current at the centre?
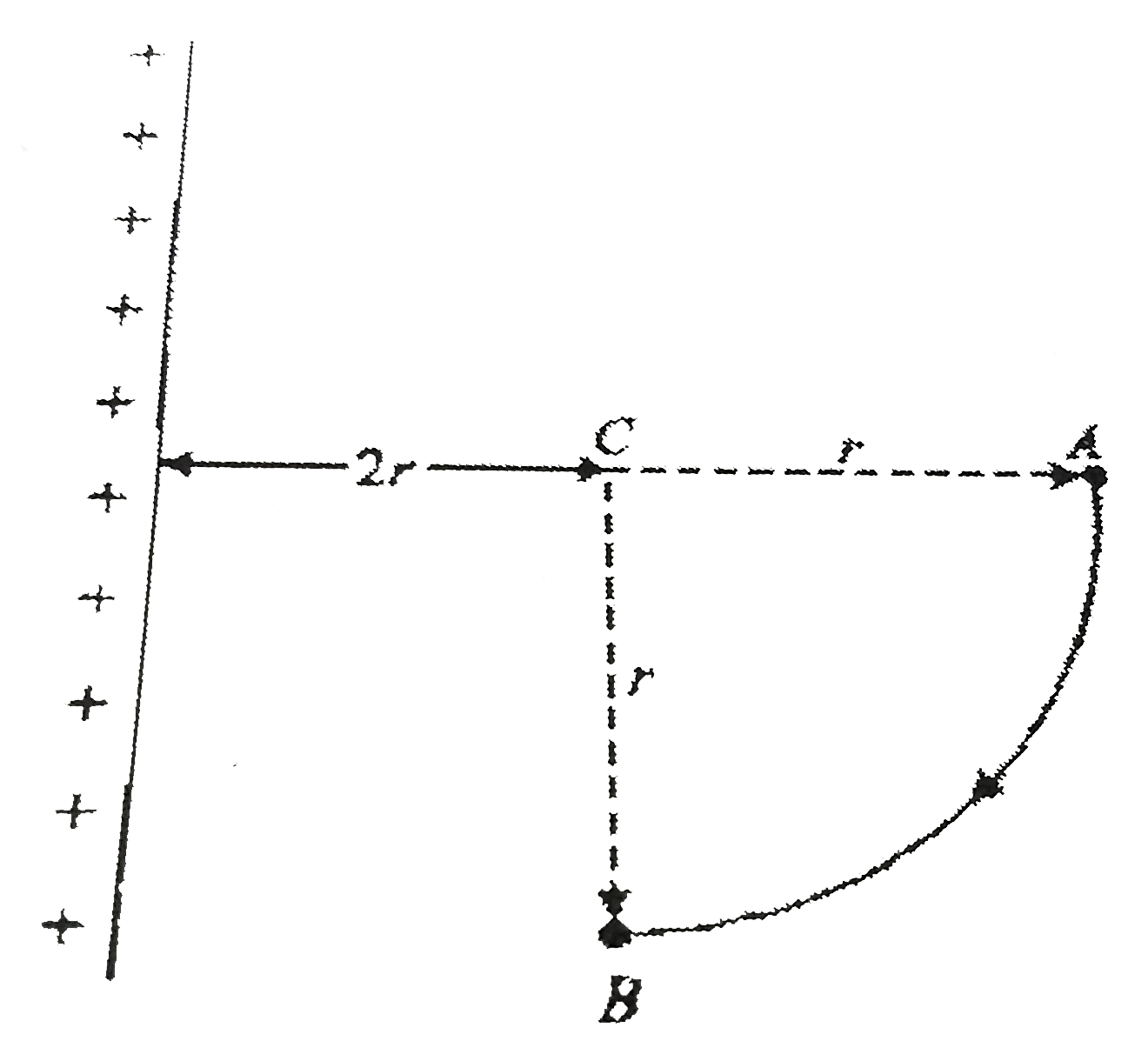
View SolutionA charge q0 is transported from point A to B along the arc AB with centre at C as shown in figure near a long charged wire with linear density A. lying in the same plane. Find the work done in doing so.
View SolutionA wire carrying a current I is bent into the shape of an exponential spiral, r=eθ, from θ=0 to θ=2π as shown in figure (a0 . To complete a loop, the ends of the spiral are connected by a straight wire along the x− axis. Find the magnitude and direction of →B at the origin.

View SolutionA circular loop of radius r carries a current i.How should a long, straight wire carrying a current 3i be placed in the plane of the circle so that the magnetic field at the centre of the loop becomes zero?
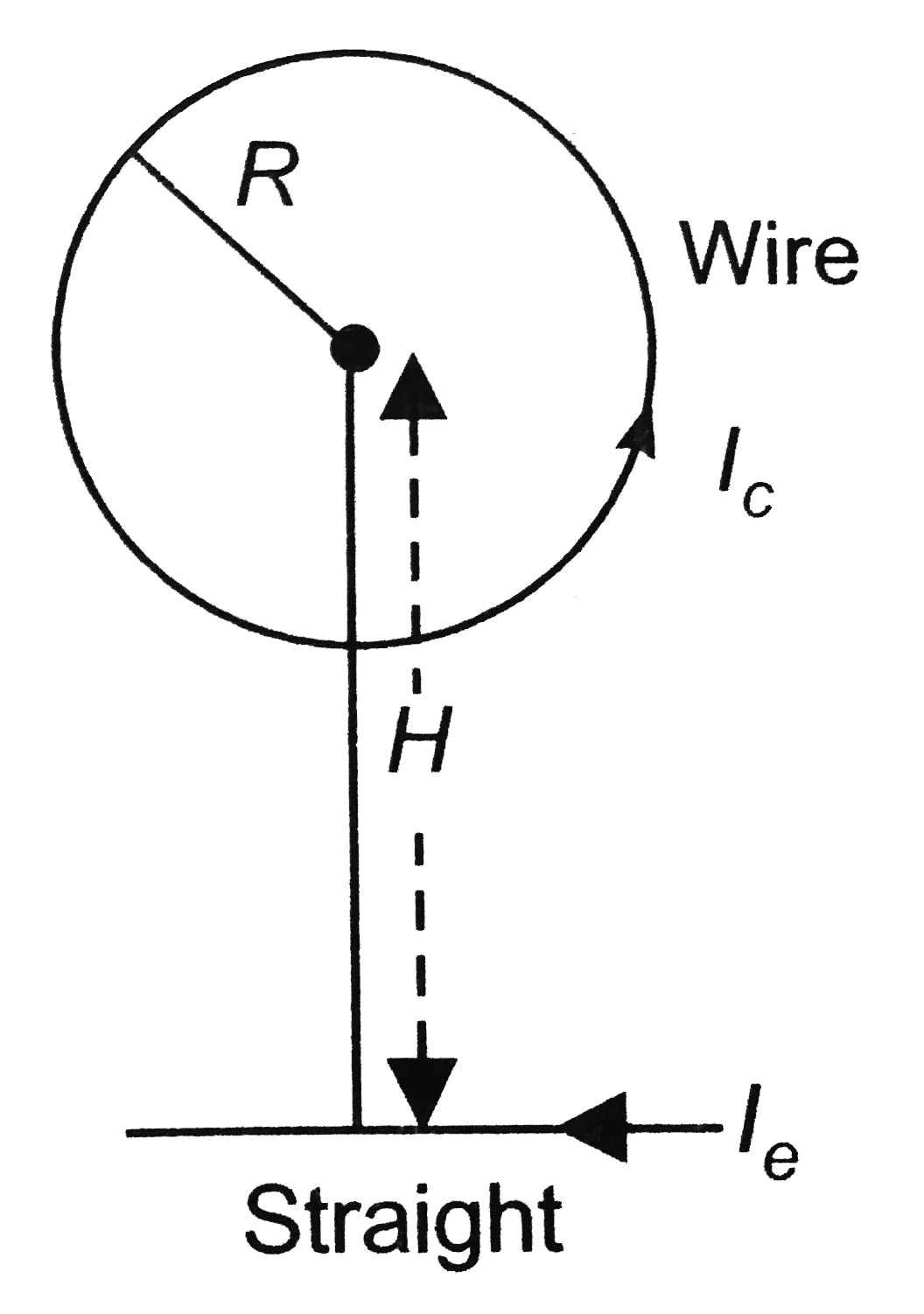
View SolutionCircular loop of a wire and a long straight wire carry current Ic and Ierespectively as shown in figure. Assuming that these are placed in the same plane. The magnetic field will be zero at the centre of the loop when the separation H is:
View Solution
