A wire carrying current I has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicicular portion of radius R is lying in Y−Z plane. Magnetic field at point O is
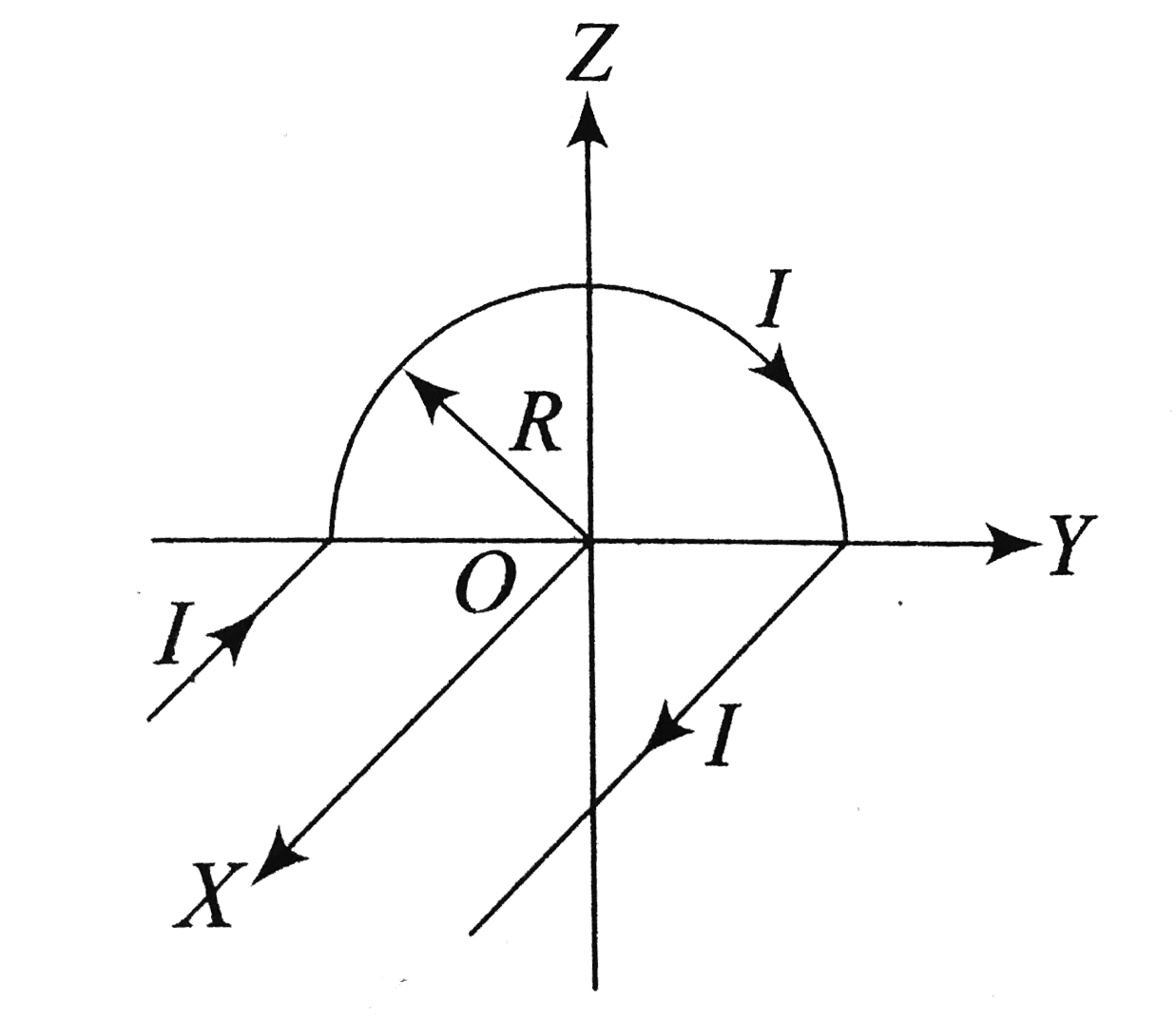
→B=−μ04πIR(πˆi−2ˆk)
→B=−μ04πIR(πˆi+2ˆk)
→B=μ04πIR(πˆi−2ˆk)
→B=μ04πIR(πˆi+2ˆk)
The correct Answer is:b
Magnetic field at O due to the semicircular loop is:
→B1=μ0Iπ4πR(−ˆi)
Magnetic field at O due to semi-infinite long wires will be:
→B2=2[μ0I4πR](−ˆk)
Then, the net magnetic field at O will be :
→B=→B1+→B2=μ0Iπ4πR(−ˆi)+μ0I4πR(−2ˆk)
=−μ0I4πR(πˆi+2ˆk)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)
28 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (D. MULTIPLE CHOICE QUESTIONS)
10 Videos
- MOVING CHARGES AND MAGNETISMBOOK - MODERN PUBLICATIONCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - COMPETITION FILE (A. MULTIPLE CHOICE QUESTIONS)
38 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
- NUCLEIBOOK - MODERN PUBLICATIONCHAPTER - NUCLEIEXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
15 Videos
Similar Questions
A conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

View Solution(a) Find the magnetic field at the point O if the wire carrying a current i has the shape shown. The radius of the current part of the wire is R, the linear parts of the wire are very long.
(i)
(ii)
(iii)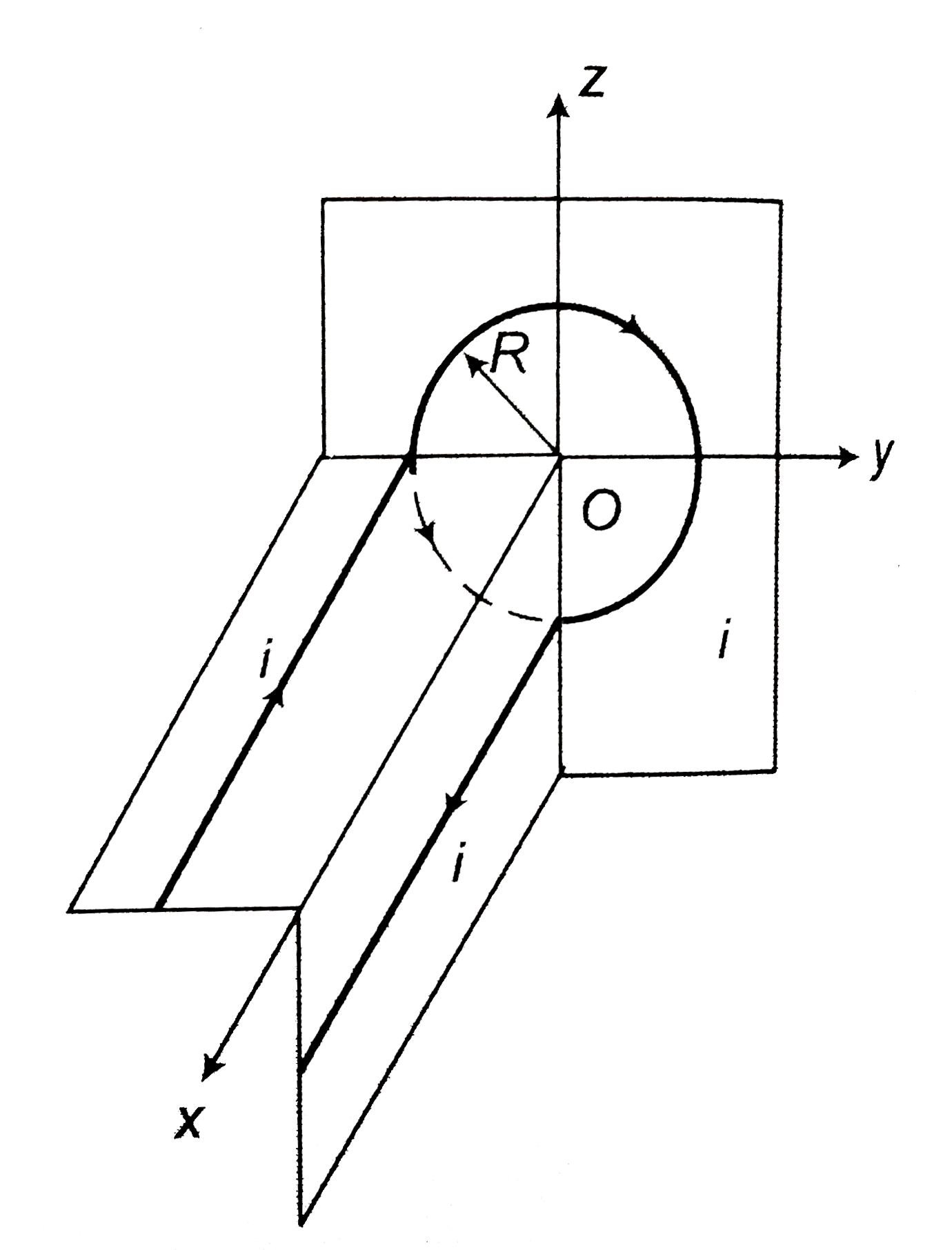
(b) A long straight wire along the z-axis carriers a current i in negative z-direction. Find magnetic field in vector from at a point having co-ordinates (x,y) on z=0 plane.
(c) A non-coplaner loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop of length 2a. find unit vector along magnetic field magnetic filed at the point P(a,0,a).
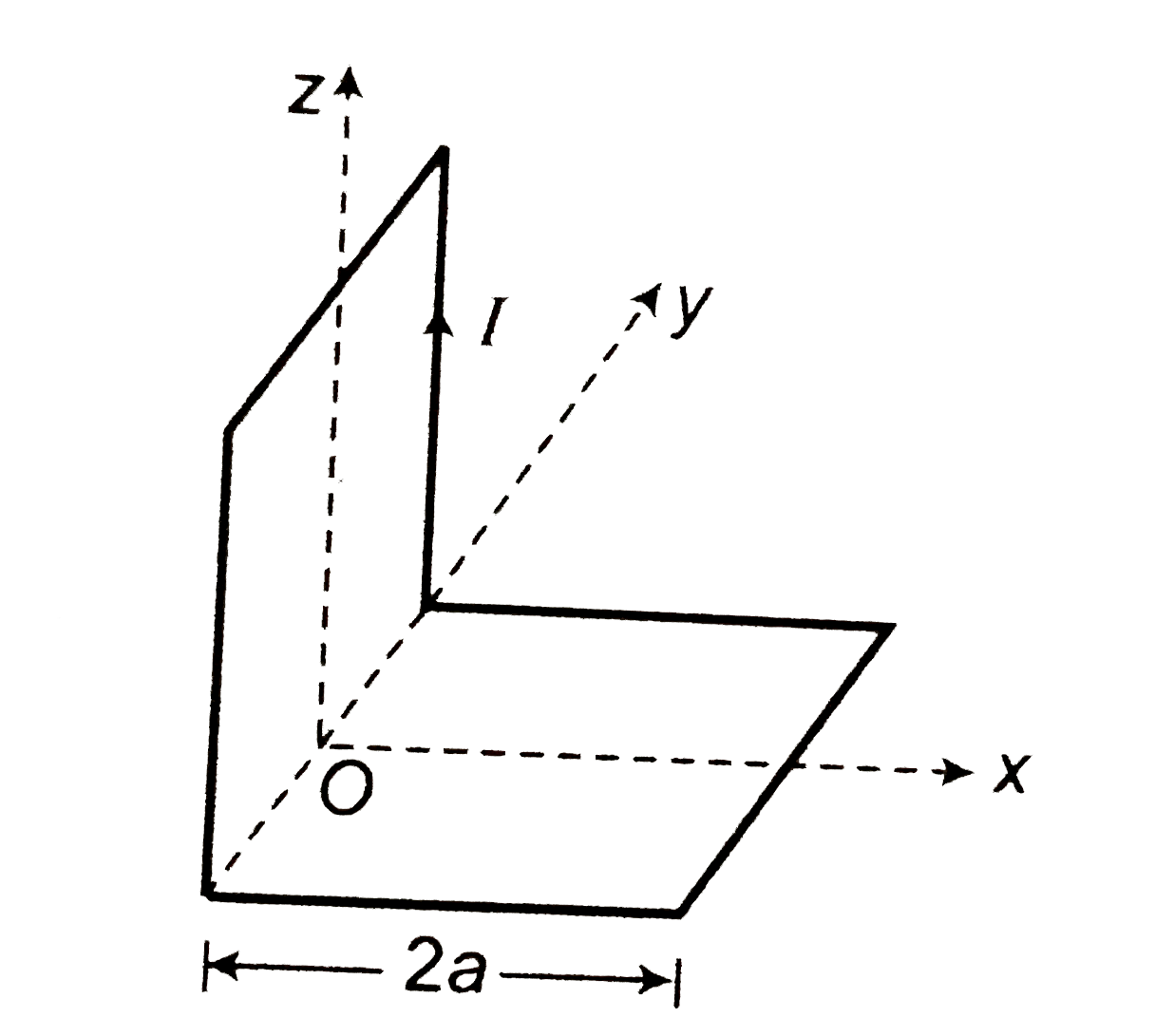
View Solution
Knowledge Check
A wire carrying current I has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicicular portion of radius R is lying in Y−Z plane. Magnetic field at point O is
 A→B=−μ04πIR(μˆi×2ˆk)B→B=−μ04πIR(μˆi+2ˆk)C→B=−μ04πIR(πˆi−2ˆk)D→B=−μ04πIR(πˆi+2ˆk)
A→B=−μ04πIR(μˆi×2ˆk)B→B=−μ04πIR(μˆi+2ˆk)C→B=−μ04πIR(πˆi−2ˆk)D→B=−μ04πIR(πˆi+2ˆk)A wire carrying current I has the shape as shown in adjoining figure. Linear parts of the wire are very long and parallel to X-axis while semicircular portion of radius R is lying in Y-Z plane. Magnetic field at point O is
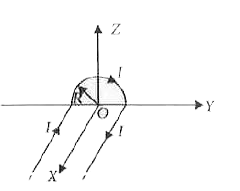 A→B=−μ04πIR(πˆi+2ˆk)B→B=μ04π.IR(πˆi−2ˆk)C→B=μ04π.IR(πˆi−2ˆk)D→B=−μ04π.IR(πˆi−2ˆk)
A→B=−μ04πIR(πˆi+2ˆk)B→B=μ04π.IR(πˆi−2ˆk)C→B=μ04π.IR(πˆi−2ˆk)D→B=−μ04π.IR(πˆi−2ˆk)A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
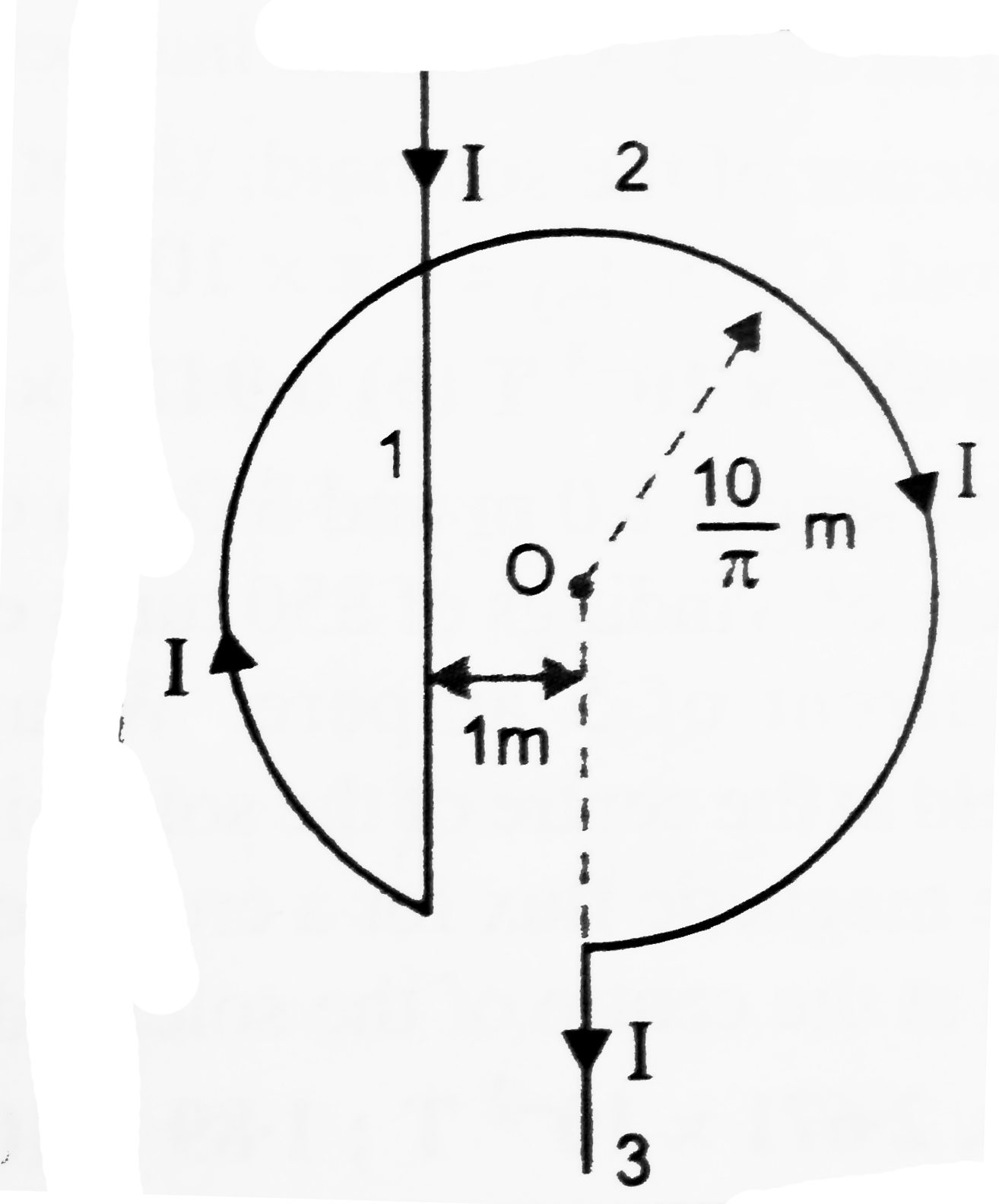
A long straight wire carrying current I is bent into the shape as shown in the figure. The circular portion of the wire has radius (10/π)m. The centre of this circle is at a distance 1m from the straight portion of the wire. What is the magnitude of the magnetic field at the centre of the circular portion? Given π2=10.
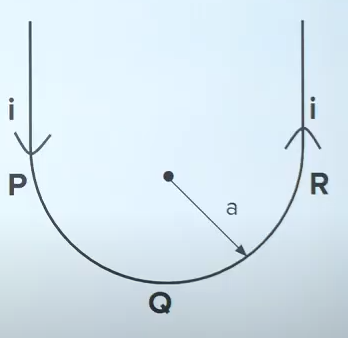
View SolutionIn figure shown U-shaped wire a current i is flowing as shown. Section PQR is a semicircle of radius a.If O is origin then find magnetic field at O
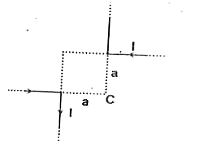
View SolutionTwo inflinitely long wires carrying current I, are bent as shown in the figure. Find the magnetic induction at point C.
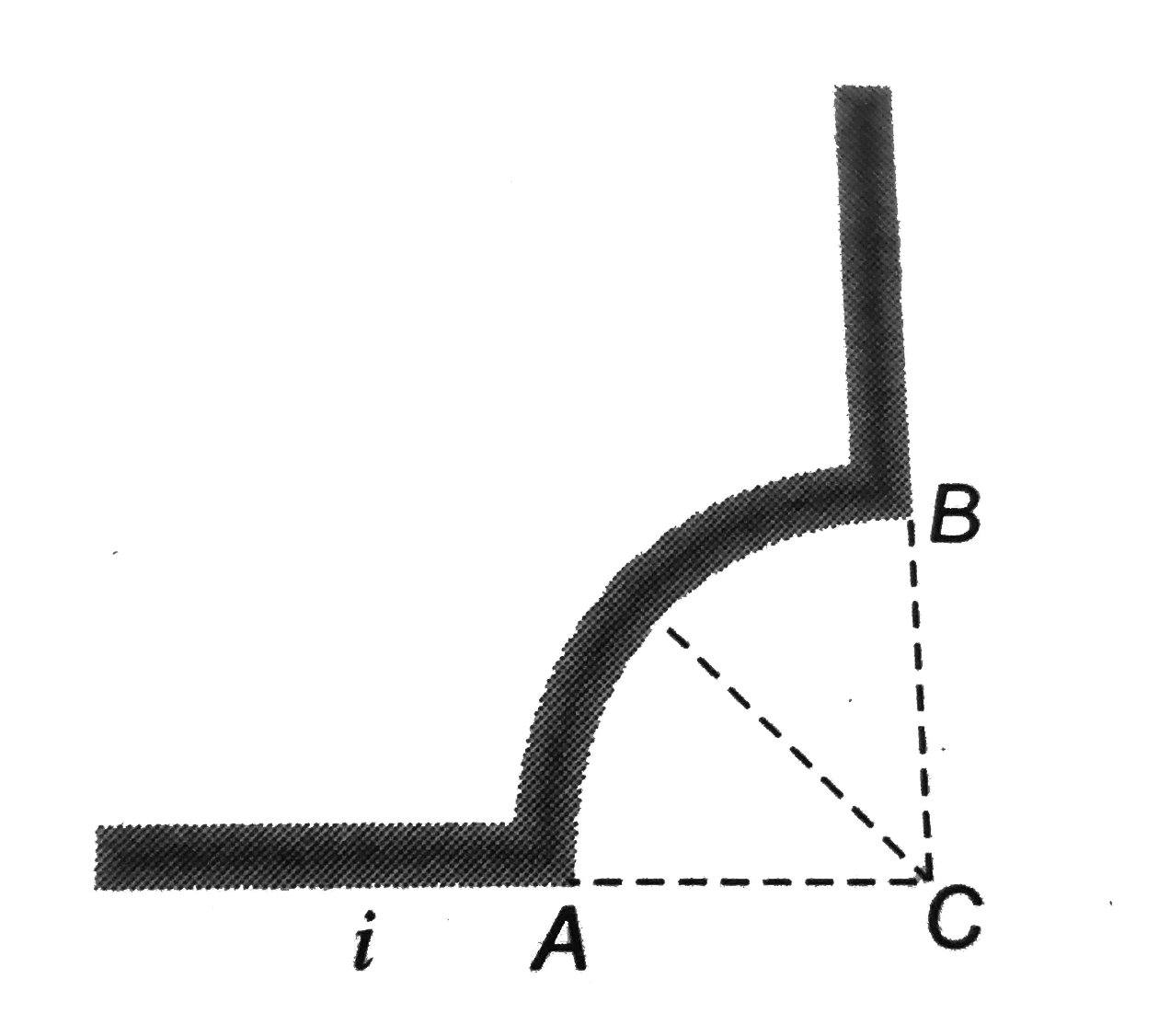
View SolutionA wire carrying current i is shaped as shown. Section AB is a quarter circle of radius r. The magnetic field is directed
View Solution
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius R
View Solution
