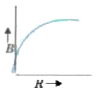
A charge $Q$ is uniformly distributed over the surface of non - conducting disc of radius $R$ . The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:

A

ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

To calculate magnetic field at the centre of disc we need to select one ring segment of radius x and thickness dx on the surface of disc. Charge on this ring segment can be written as follows:
$d q = \frac{Q}{π R^{2}} 2 π x d x = \frac{2 Q}{R^{2}} x d x$
Its equivalent current due to rotation can be written as follows:
$d i = \frac{d q}{T} = \frac{\frac{2 Q}{R^{2}} x d x}{\frac{2 π}{ω}} = \frac{Q ω x d x}{π R^{2}}$
Magnetic field at the centre of disc due to ring segment only can be written as follows:
$d B = \frac{μ_{0} (d i)}{2 x} = \frac{μ_{0} Q ω x d x}{2 x \times π R^{2}} = \frac{μ_{0} Q ω}{2 π R^{2}} d x$
All such ring segments will produce magnetic field in the same direction at the centre of disc. Hence, net magnetic field at the centre can be calculated by integrating the above result.
$\Rightarrow B = \int d B = \frac{μ_{0} Q ω}{2 π R^{2}} R \int 0 d x = \frac{μ_{0} Q ω}{2 π R}$
Magnetic field at the centre of disc is inversely proportional to its radius for a given charge magnitude. Thus, option (a) is correct.

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Radius of gyration of disc rotating about an axis perpendicular to its plane passing through through its centre is (If R is the radius of disc)
A $\frac{R}{2}$
B $\frac{R}{\sqrt{2}}$
C $\frac{R}{\sqrt{3}}$
D $\frac{R}{3}$
Question 2 - Select One
Radius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
A $R / \sqrt{2}$
BR/2
C $\sqrt{2}$ R
D2R
Question 3 - Select One
Circular disc of mass 2 kg and radius 1 m is rotating about an axis perpendicular to its plane and passing through its centre of mass with a rotational kinetic energy of 8 J. The angular momentum is (Js) is
A8
B4
C2
D1

MODERN PUBLICATION-MOVING CHARGES AND MAGNETISM-COMPETITION FILE (B. MULTIPLE CHOICE QUESTIONS)

Home
Ask Doubt
Profile