A wire is bent into the shape shown in fig and the magnetic field is measured at P1 when the current in the wire is I. The same wire is then formed into the shape shown in the Fig and the magnetic field is measured at point P2 when the current is again I. If the total length of wire is the same in each case, what is the ratio of B1/B2 ?
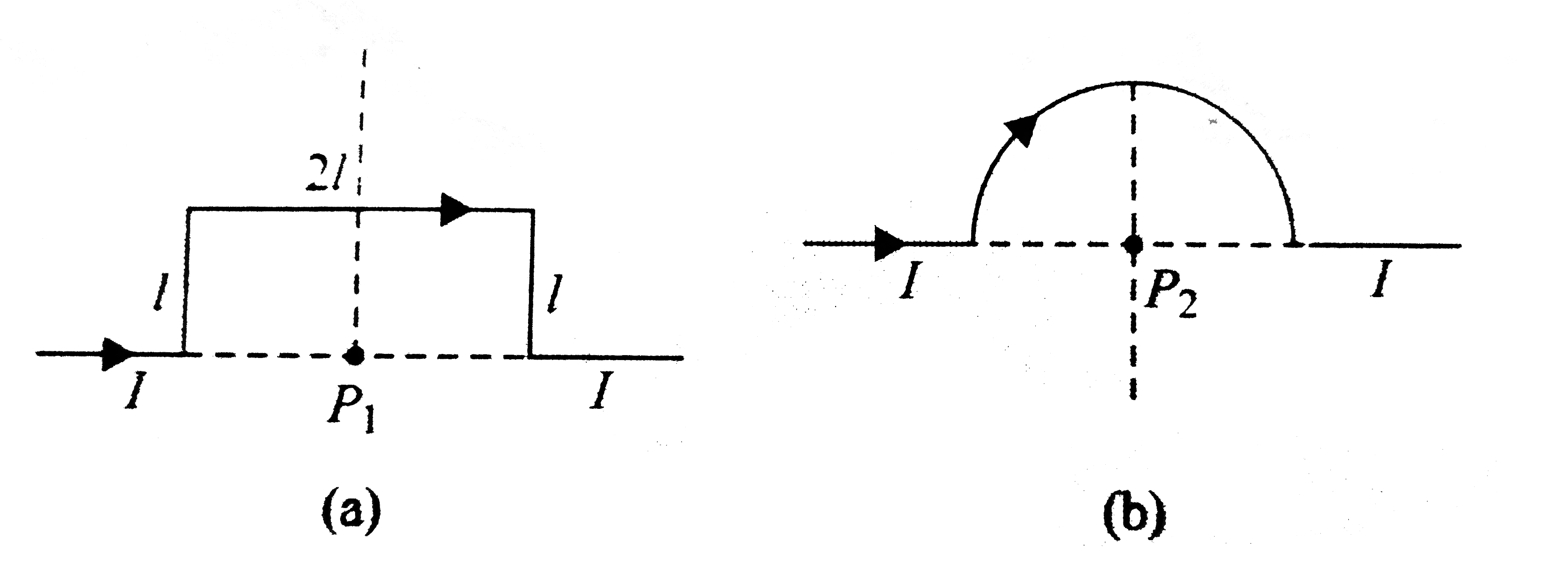

Video Solution
Text Solution
Case I: →Bnet=→B1+→B2+→B3
=[μ0I4πl[0+sin45∘]+μ0I4πl[sin45∘+sin45∘]
+μ0I4πl[0+sin45∘]]⊗

∴∣∣→Bnet∣∣=μ0I√2πl=B1
CaseII: 2πr=4l⇒2lπ
Magnetic field at the centre of semicircle,
Bsemicircle=μ0I4r=μ0Iπ8l=B2
B1B2=μ0I√2πl×8lμ0Iπ=4√2π2.
|
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example
20 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
Knowledge Check
A long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is
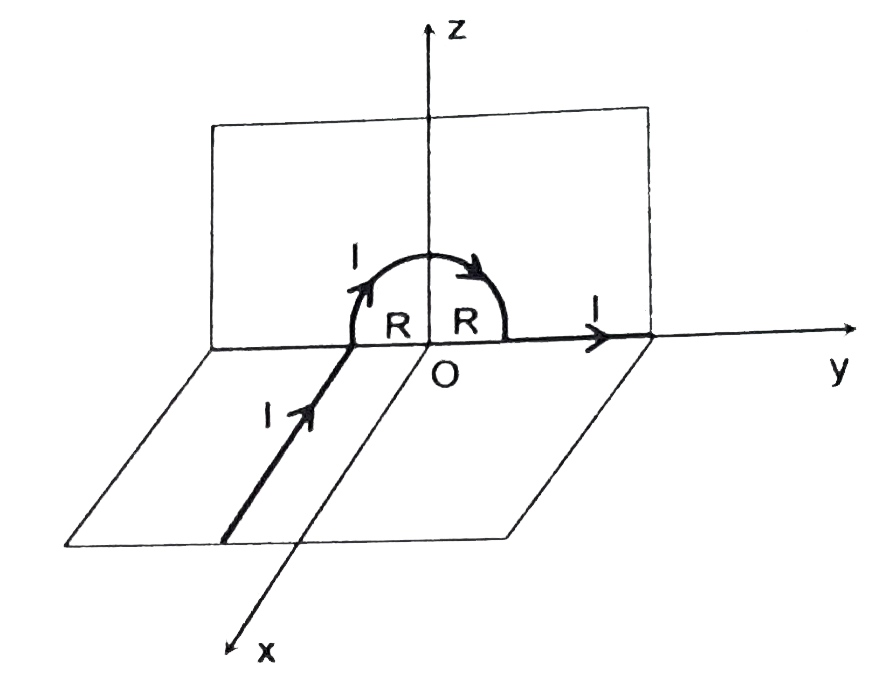 Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2
Aμ0I4πR√1+π2Bμ0I4πR√2+π2Cμ0I4πR√4+π2Dμ0I4πR√9+π2The magnetic field at O due to current in the infinite wire forming a loop as a shown in Fig.
 Aμ0I2πd(cosϕ1+cosϕ2)Bμ04π2Id(tanθ1+tanθ2)Cμ04πId(sinϕ1+sinϕ2)Dμ04πId(cosθ1+cosθ2)
Aμ0I2πd(cosϕ1+cosϕ2)Bμ04π2Id(tanθ1+tanθ2)Cμ04πId(sinϕ1+sinϕ2)Dμ04πId(cosθ1+cosθ2)For the current carrying wire, show that the magnetic field at P is
 Aμ0i4π(3π2R+√2d)⊙Bμ0i4π(3π2R−√2d)⊗Cμ0i4π(3π2R−√2d)⊙Dμ0i4π(3π2R+√2d)⊗
Aμ0i4π(3π2R+√2d)⊙Bμ0i4π(3π2R−√2d)⊗Cμ0i4π(3π2R−√2d)⊙Dμ0i4π(3π2R+√2d)⊗
The segment of wire shown in figure carries a current of i=5 A. The magnetic field (in Tesla) at the point P is
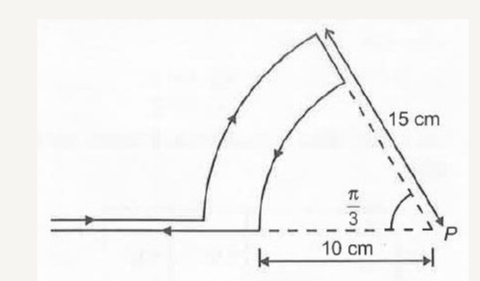
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be
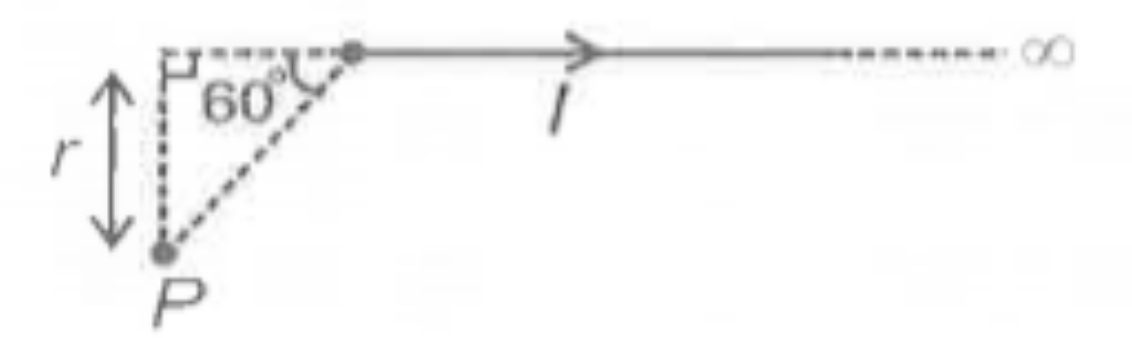
View SolutionA wire of infinite length bent as shown in figure carries current l. What is the magnetic field at the point P ?
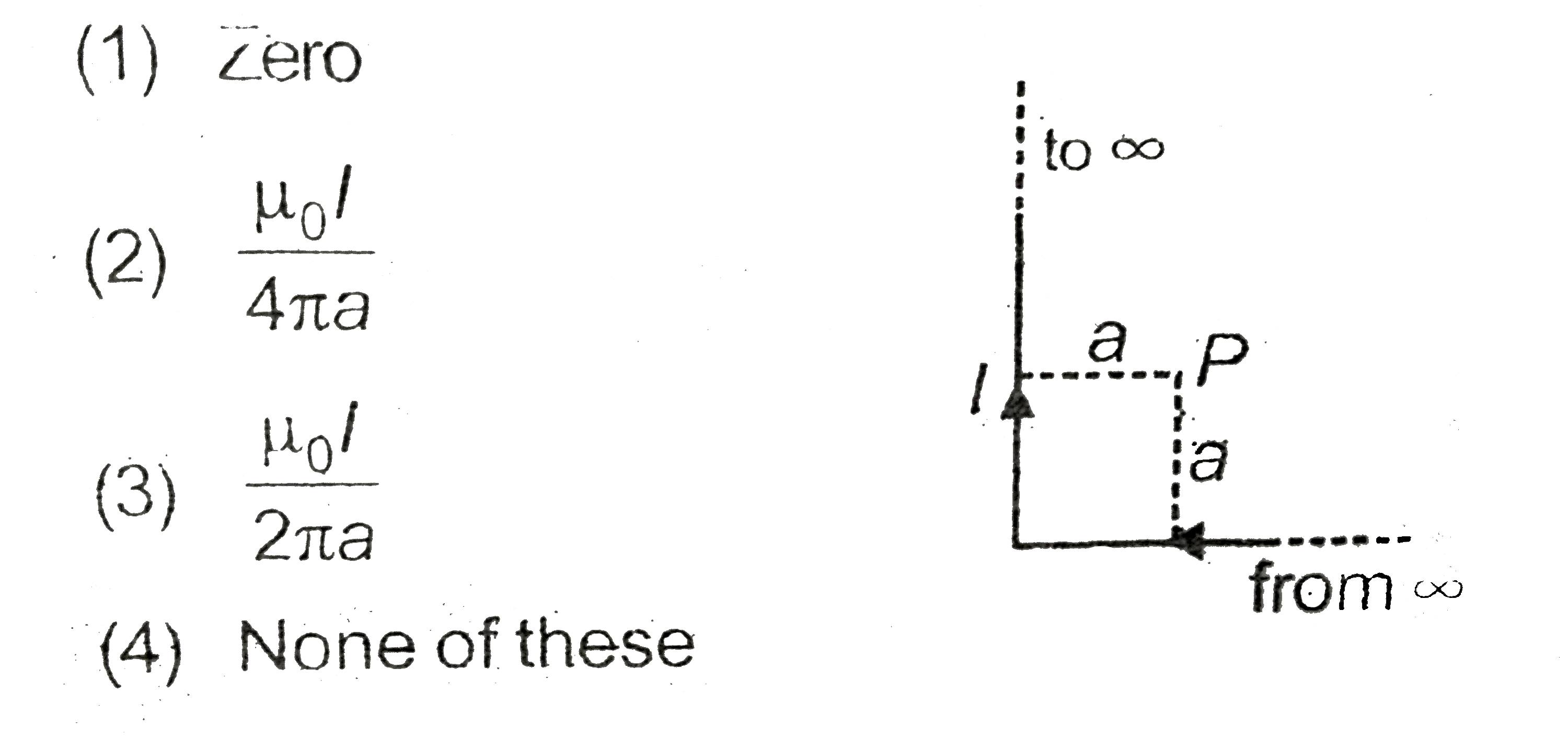
View SolutionTwo infinitely long wires each carrying current I along the same direction are made into the geometry as shown in the figure. The magnetic field at the point P is

View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
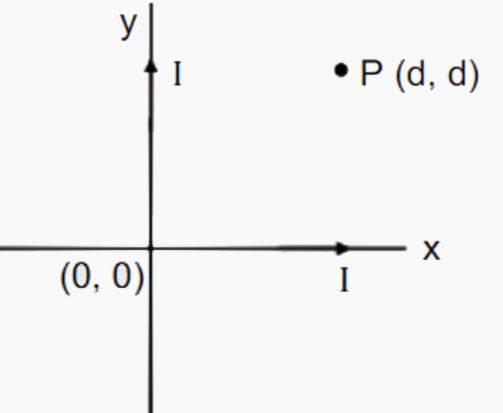
View Solution

