A wire lying along y-axis from y=0 to y=1m carries a current of 2mA in the negative y-direction. The wire lies in a non uniform magnetic fiedl given by B=(0.3Tm)yˆi+(0.4Tm)yˆj. The magnetic force on the entire wire is
−3×10−4ˆjN
6×10−3ˆkN
−3×10−4ˆkN
3×10−4ˆkN
The correct Answer is:D
To solve the problem of finding the magnetic force on a wire lying along the y-axis in a non-uniform magnetic field, we can follow these steps:
Step 1: Understand the Given Information
- The wire extends from y=0 to y=1 meter.
- The current I=2mA=2×10−3A flows in the negative y-direction.
- The magnetic field is given by B=(0.3T/m)y^i+(0.4T)^j.
Step 2: Identify the Magnetic Force Formula
The magnetic force F on a current-carrying wire in a magnetic field is given by:
F=I∫B×dl
where dl is the differential length vector along the wire.
Step 3: Set Up the Differential Length Element
Since the wire is along the y-axis, the differential length element can be expressed as:
dl=dy^j
Step 4: Calculate the Magnetic Field at Each Point
The magnetic field B can be evaluated at any point along the wire. Since y varies from 0 to 1, we have:
B=(0.3y)^i+(0.4)^j
Step 5: Calculate the Cross Product
Now, we need to calculate the cross product B×dl:
B×dl=∣∣
∣
∣∣^i^j^k0.3y0.40010∣∣
∣
∣∣
Calculating this determinant gives:
B×dl=^k(0.3y⋅1−0.4⋅0)=0.3y^k
Step 6: Substitute into the Force Equation
Now substitute this into the force equation:
F=I∫10(0.3y^k)dy
This simplifies to:
F=I^k∫100.3ydy
Step 7: Perform the Integration
Now, perform the integration:
∫100.3ydy=0.3(y22)10=0.3⋅122=0.15
Step 8: Calculate the Total Force
Now substitute back into the force equation:
F=I^k(0.15)=(2×10−3A)^k(0.15)=3×10−4^kN
Step 9: Final Result
Thus, the magnetic force on the entire wire is:
F=3×10−4^kN
- The wire extends from y=0 to y=1 meter.
- The current I=2mA=2×10−3A flows in the negative y-direction.
- The magnetic field is given by B=(0.3T/m)y^i+(0.4T)^j.
The magnetic force F on a current-carrying wire in a magnetic field is given by:
F=I∫B×dl
where dl is the differential length vector along the wire.
Since the wire is along the y-axis, the differential length element can be expressed as:
dl=dy^j
The magnetic field B can be evaluated at any point along the wire. Since y varies from 0 to 1, we have:
B=(0.3y)^i+(0.4)^j
Now, we need to calculate the cross product B×dl:
B×dl=∣∣
∣
∣∣^i^j^k0.3y0.40010∣∣
∣
∣∣
Calculating this determinant gives:
B×dl=^k(0.3y⋅1−0.4⋅0)=0.3y^k
Now substitute this into the force equation:
F=I∫10(0.3y^k)dy
This simplifies to:
F=I^k∫100.3ydy
Now, perform the integration:
∫100.3ydy=0.3(y22)10=0.3⋅122=0.15
Now substitute back into the force equation:
F=I^k(0.15)=(2×10−3A)^k(0.15)=3×10−4^kN
Thus, the magnetic force on the entire wire is:
F=3×10−4^kN
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
A conducting wire bent in the from of a parabola y2=2x carries a current i=2A as shown in figure This wire is placed in a unifrom magnetic field
→B=−4ˆk Tesla The magnetic force on the wire is (newton)
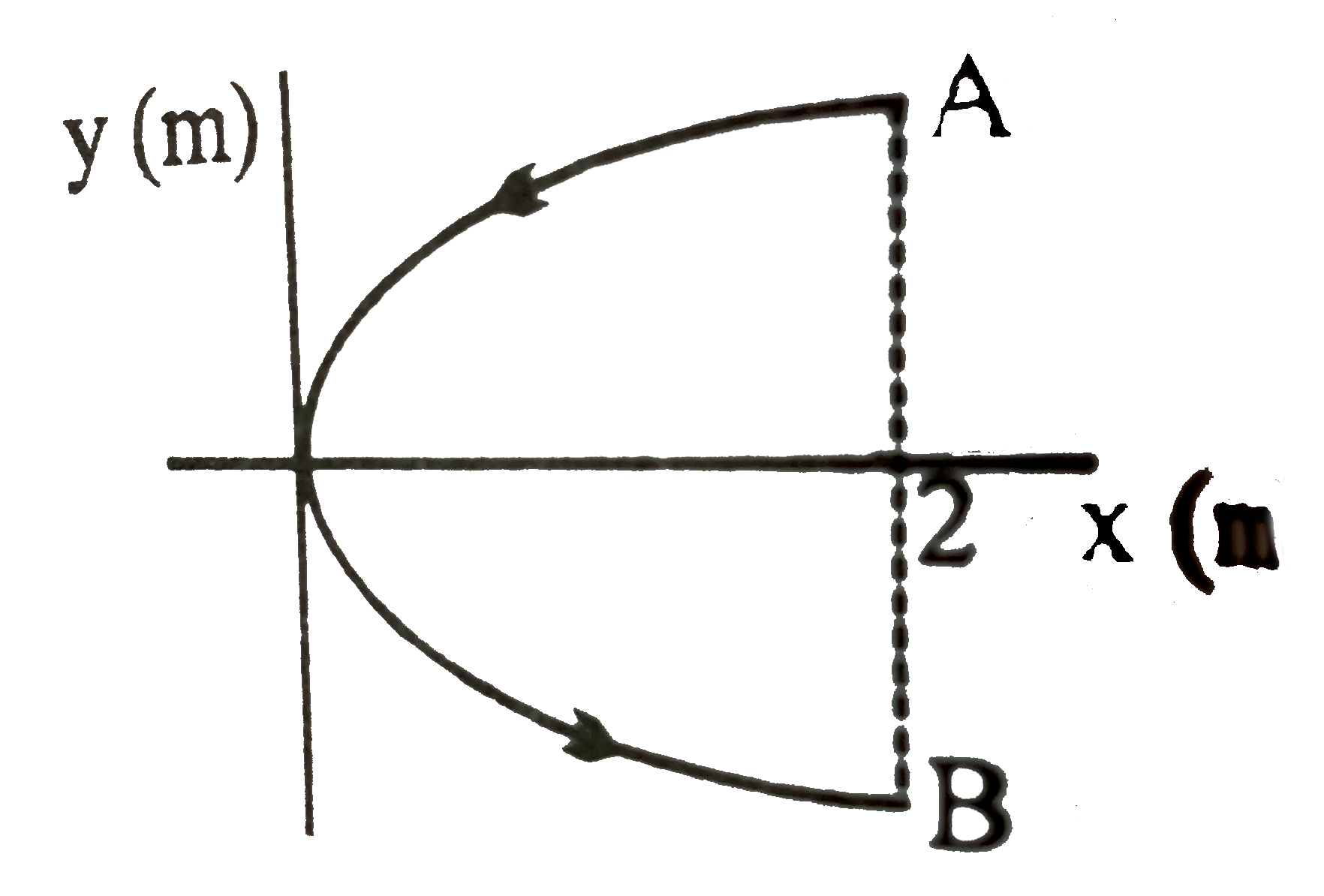 .
.
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View Solution
Knowledge Check
An 8 cm long wire carrying a current of 10 A is placed inside a solenoid perpendicular to its axis. If the magnetic field inside the solenoid is 0.3 T, then magnetic force on the wire is
A0.14NB0.24NC0.34ND0.44N
A long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA wire bent in the form a right angled triangle PQR, carries a current 1A. It is placed in a region of a uniform magnetic field B=0.2T. If PR=1m, the net force on the wire is

View SolutionA 3⋅0cm wire carrying a current of 10A is placed inside a solenoid perpendicular to its axis. The magnetic field inside the solenoid is given to be 0⋅27T. What is the magnetic force on the wire?
View SolutionA wire along the x-axis carries a current of 3.50A in the negative direction. Calculate the force (expressed in term of unit vectors) on a 1.00cm sectioin of the wire exerted by these magnetic fiels.
a. B=−(0.65T)ˆjb.B=+(0.56T)hatk c. B=−(0.31T)ˆj
d. B=0.33Tˆi−(0.28t)ˆk e. B=+(0.74T)ˆj−0(0.36T)ˆk
View SolutionThe figure shows a loop of wire carrying a current i as shown. There exists a uniform magnetic field along x-axis given by →B=B0ˆi. If the length of each side is a, then
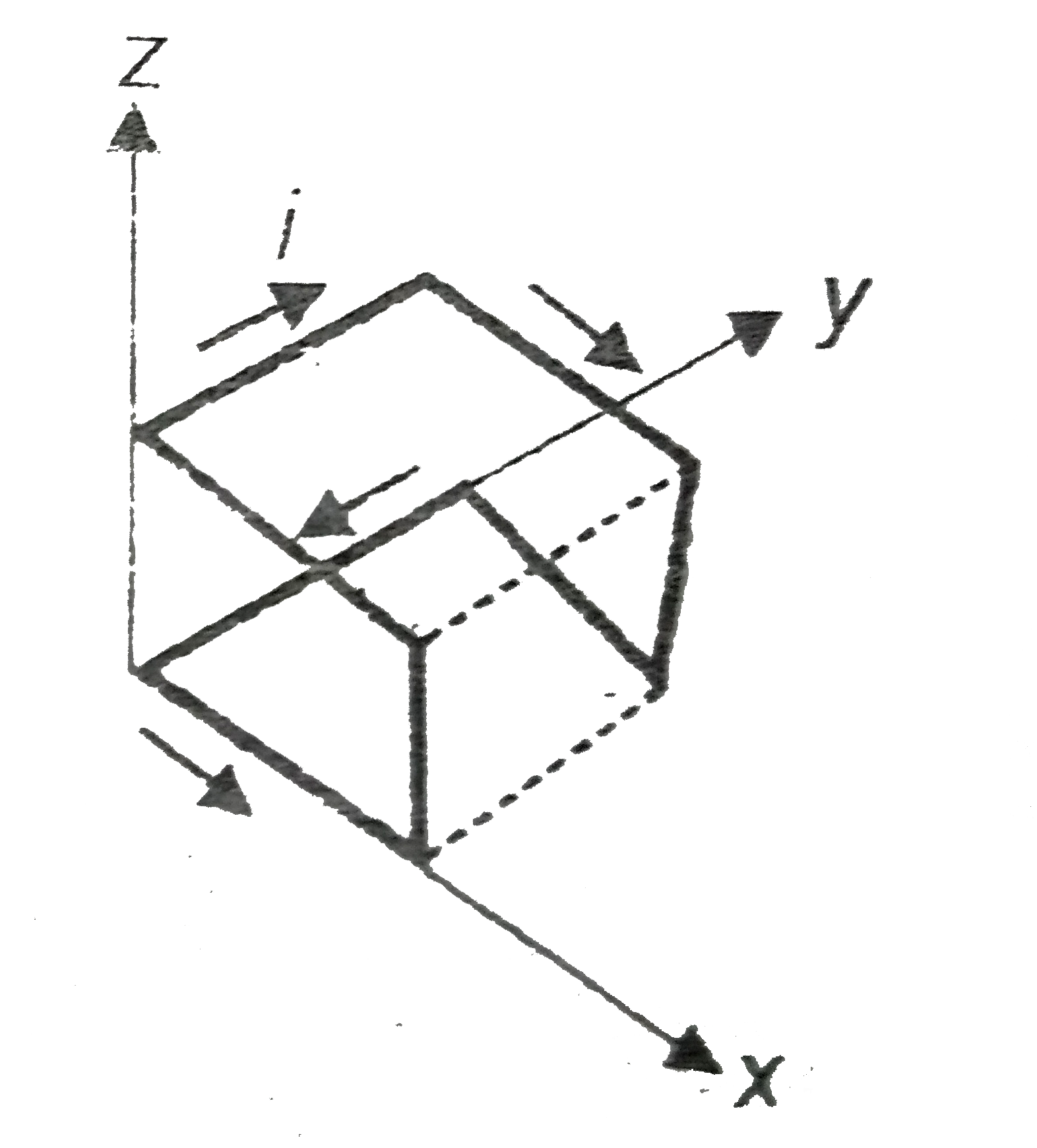
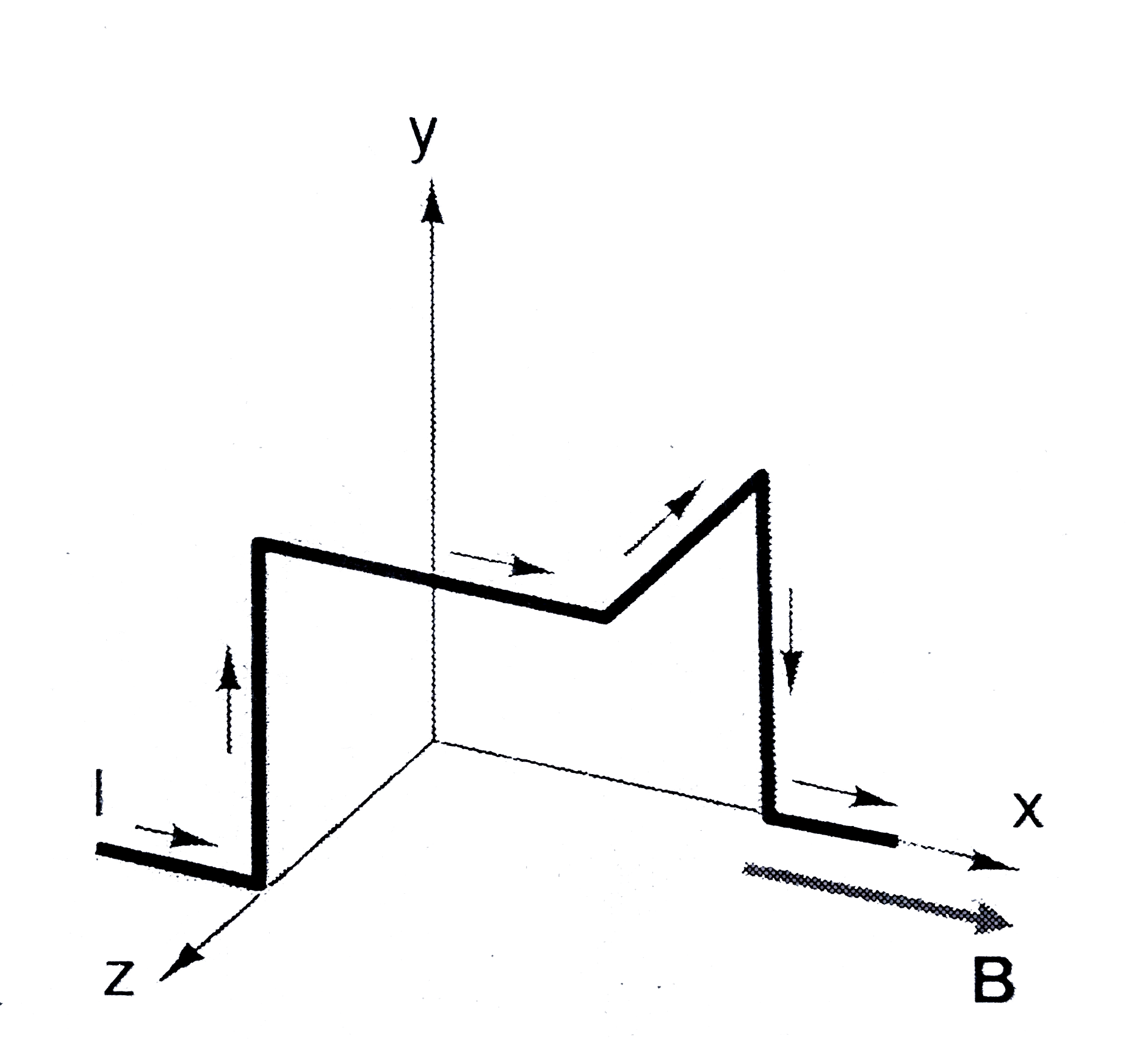
View SolutionA long wire carrie scurrent of 25 A parallel to the positive x axis, except for three of the four segments that follow the edges of a cube of side 0.4m, as shown in figure. The wire is in a uniform magnetic field of 2.0T directed paralled to the positice x axis. What is the net magnetic force on the wire (in newton) ?
View SolutionA wire carrying a current i is placed in a uniform magnetic field in the form of the curve y=asin(πxL)0≤x≤2L. The force acting on the wire is
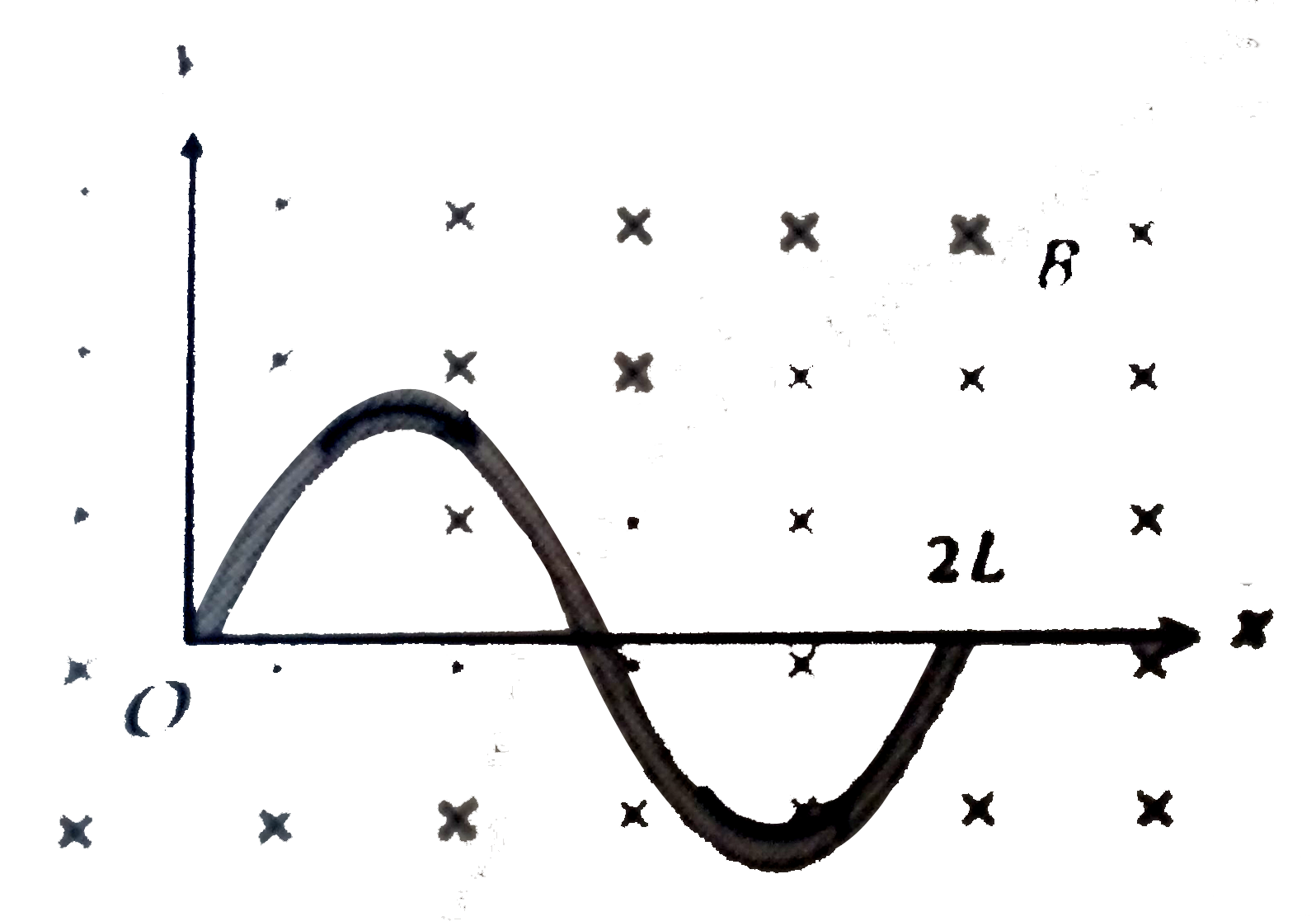
View Solution
