A wire of identical length and cross-section is used for fixed vibration between two rigid supports slightly more than the length of string. The wire has Young's Modulus =2Y and mass per unit length =μ/2 and v is the fundamental frequency. Find frequency in the 2nd mode of this wire.
v
2v
3v
6v
The correct Answer is:B
Topper's Solved these Questions
- STATIONARY WAVESBOOK - TARGET PUBLICATIONCHAPTER - STATIONARY WAVESEXERCISE - COMPETITIVE THINKING
123 Videos
- SEMICONDUCTORSBOOK - TARGET PUBLICATIONCHAPTER - SEMICONDUCTORSEXERCISE - Evaluation Test
17 Videos
- SURFACE TENSION BOOK - TARGET PUBLICATIONCHAPTER - SURFACE TENSION EXERCISE - EVALUATION TEST
21 Videos
Similar Questions
A metal wire of length jl and area of cross - section A is fixed between rigid supports negligible tension . If this is cooled. The tension in the wire will be
View SolutionTwo wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be

View Solution
Knowledge Check
Two wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be
 AY1+Y2BY1−Y22CY1Y2Y1+Y2D√Y1Y2
AY1+Y2BY1−Y22CY1Y2Y1+Y2D√Y1Y2Two wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
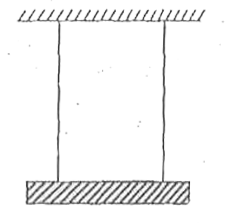 AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2
AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2A wire of natural length l, young's modulus Y and ares of cross-section A is extended by x. Then, the energy stored in the wire is given by
A12YAlx2B13YAlx2C12YlAx2D12YAl2x2
Two wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
View SolutionTwo wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
View SolutionA string is fixed between two rigid support. Mass per unit length of the string is lambda. Now the tension in the wire is decreased by 19%. The percentage decrease in frequency will be
View SolutionA string is fixed between two rigid support. Mass per unit length of the string is lambda. Now the tension in the wire is decreased by 19%. The percentage decrease in frequency will be
View SolutionA wire of natural length l, young's modulus Y and area of cross-section A is extended by x. Then, the energy stored in the wire is given by
View Solution
