A wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
Let during the stretching of the wire, its extension at an instant of tme is x and it is further stretched by dx. The restoring force acting at that instant is
Y=F/Ax/L⇒F=Yx1×L×A

The small amount of work done during the stretching by dx by the applied force
dW=Fdx=YxALdx
Total work done for stretching for distance x can be by integrating above equation.
W=∫x0YxAdxL=YAL∫x0xdx=YAx22L
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Fill In The Blanks
1 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - SCQ_TYPE
6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - Linked Comprehension
30 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
Similar Questions
A metallic rod of length l and cross-sectional area A is made of a material of Young's modulus Y. If the rod is elongated by an amount y,then the work done is proportional to
View SolutionA uniform wire of length 6m and a cross-sectional area 1.2 cm2 is stretched by a force of 600N . If the Young's modulus of the material of the wire 20×1010Nm−2 , calculate (i) stress (ii) strain and (iii) increase in length of the wire.
View Solution
Knowledge Check
Young's modulus of a wire depends on
Adiameter of the wireBmass hanging from the wireClength of the wireDÂ material of the wireA steel wire of length 4.5 m and cross-sectional area 3×10−5m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4x10−5m2 under a given load. The ratio of the Young's modulus of steel to that of copper is
A1.3B1.5C1.7D1.9
A point mass m is suspended at the end of a massless wire of length l and cross section. If Y is the Young's modulus for the wire, obtain the frequency of oscillation for the simple harmonic motion along the vertical line.
View SolutionA steel wire of length 4.7m and cross-sectional area 3×10−6m2 stretches by the same amount as a copper wire of length 3.5m and cross-sectional area of 4×10−6m2 under a given load. The ratio of Young's modulus of steel to that of copper is
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
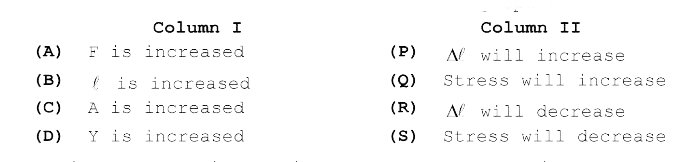
View SolutionA wire of length l and cross-sectional are A is suspended at one of its ends from a ceiling. What will be its strain energy due to its own weight, if the density and Young's modulus of the material of the wire be d and Y?
View SolutionA steel wire of length l and cross sectional area A is stretched by 1 cm under a given load. When the same load is applied to another steel wire of double its length and half of its cross section area, the amount of stretching (extension) is
View SolutionA wire havinga length L and cross- sectional area A is suspended at one of its ends from a ceiling . Density and young's modulus of material of the wire are ρ and Y, respectively. Its strain energy due to its own weight is ρ2g2AL3αY. Find the vqalue of α
View Solution
