A wooden block performs SHM on a frictionless surface with frequency v0. The block carries a charge +Q on its surface. If now a uniform electric field E is switched on as shown, then SHM of the block will be
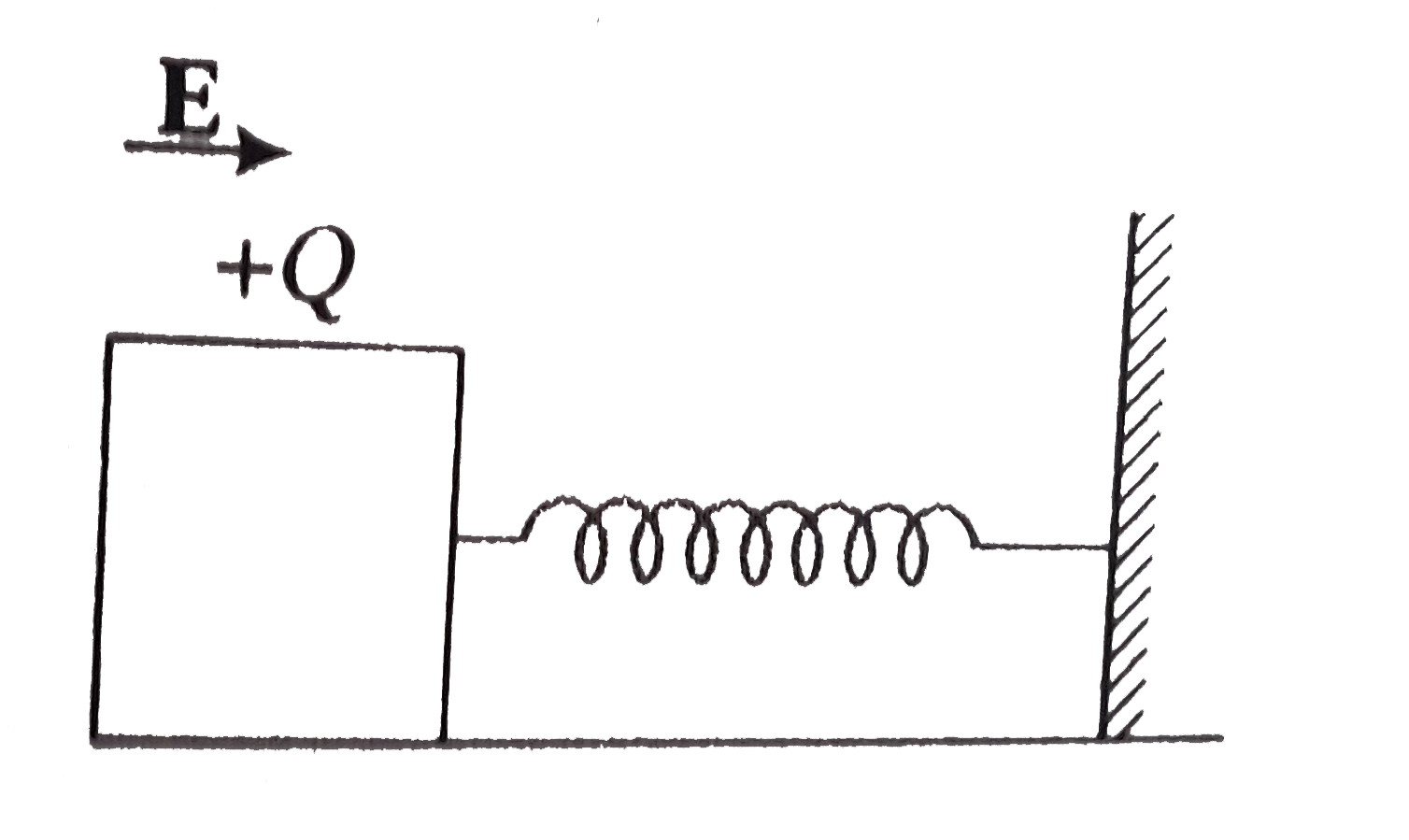
of the same frequency and with shifted mean position
of the same frequency and with the same mean position
of changed frequency and with shifted mean position
of changed frequency and with the same mean position
The frequency will be the same v=√k/m/2π. Frequency is independent of any external constant. But due to the constant foce q/E toward right, the equilibrium position gets shifted by qE/K in forward direction.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type94videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
A wooden block performs SHM on a frictionless surface with frequency, v0. The block carries a charge +Q on its surface. If now a uniform electric field →E is switched on as shwon in figure., then the SHM of the block will be
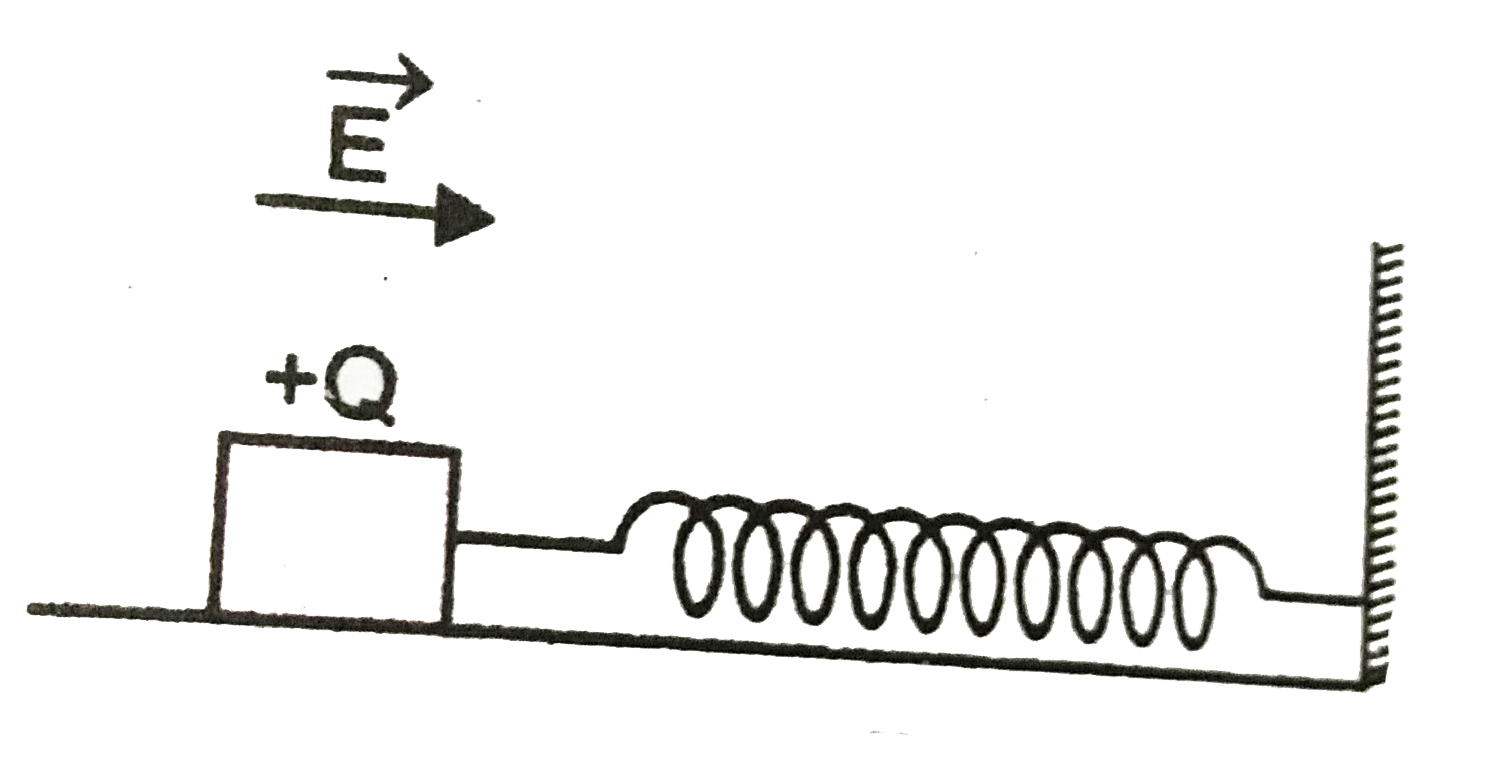 View Solution
View Solution
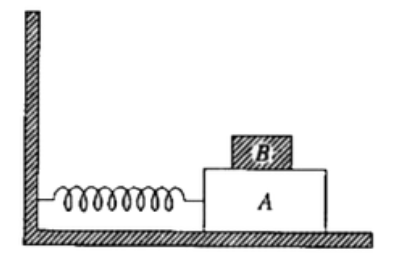
A spring block system undergoes SHM on a smooth horizontal surface, the block is now given some charge and a uniform horizontal electric field E is switched on as shown in Fig. As a resultView SolutionIn Fig. A is a large block which executes shm by sliding across a frictionless surface with a frequency n. The block B is at rest on the surface of the block μs The coefficient of static friction between the two is H. Find the maximum amplitude of oscillation of the system so that the block B does not slip.
 View Solution
View SolutionA 4.00kg block carrying a charge Q=50.0μC is connected to a spring for which k = 100 N/ m. The block lies on a frictionless horizontal track, and the system is immersed in a uniform electric field of magnitude E=5.00×105Vm, directed as shown in figure. If the block is released from rest when the spring is unstretched (at x = 0).

(a) By what maximum amount does the spring expand?
(b) What is the equilibrium position of the block?
(c) Show that the block's motion is simple harmonic and determine its period.
(d) Repeat part (a) if the coefficient of kinetic friction between block and surface is 0.2.View SolutionA block having mass 'm' and charge q is resting on a frictionless plane at distance L from the wall as shown in fig.Discuss the motion of the block when a uniform electric field E is applied horizontally towards the wall assuming that collision of the block with the wall is perfectly elastic.
View SolutionA hemispherical surface of radius R is kept in a uniform electric field E as shown in figure. The flux through the curved surface is
 View Solution
View SolutionA block of mass M has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at x = 0, in a co-ordinate system fixed to the table. A point mass m is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is x and the velocity is v. At that instant, which of the following options is/are correct?
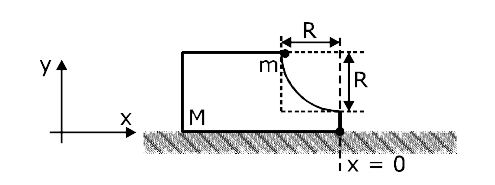 View Solution
View SolutionThe block shown in the diagram has a mass of 2μg and a charge of 2×10−9C. If the block is given an initial velocity of 2ms−1 in the x - direction at t = 0 and an electric field of 2NC−1 is switched on in the x - direction, then the range (R) of the block on the ground will be
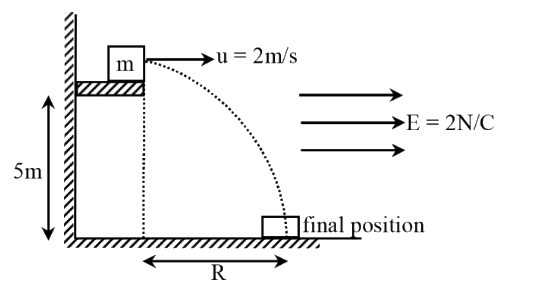 View Solution
View SolutionA block of mass m slides along a frictionless surface as shown in the figure. If it is releases from rest from A what is its speed at B?
 View Solution
View SolutionA wooden block of mass 0⋅8 kg is dragged along a level frictionless surface by a hanging block of mass 0⋅2 kg as shown in the figure . Calculate the tension in the string and the acceleration of blocks .
 View Solution
View Solution
