A block of mass M has a circular cut with a frictionless surface as shown. The block rests on the horizontal frictionless surface of a fixed table. Initially the right edge of the block is at x = 0, in a co-ordinate system fixed to the table. A point mass m is released from rest at the topmost point of the path as shown and it slides down. When the mass loses contact with the block, its position is x and the velocity is v. At that instant, which of the following options is/are correct?
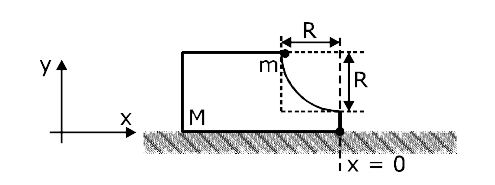
(a)The velocity of the point mass m is: v= ⎷2gR1+mM
(b)The velocity of the block M is: v=−mM√2gR
(c)The position of the point mass is: x=−√2mRM+m
(d)The x component of displacement of the center of mass of the block M is: mRM+m
The correct Answer is:A, D
Net external force acting on the system along the x-axis is zero.
∴Along the x-axis
Momentum is conserved ⇒mv=MV
From conservation of energy
Loss in GPE of particle of mass m = Gain in kinetic energy of both the masses.
⇒mgh=12mv2+12MV2⇒mgh=12mv2+12M(mvM)2
⇒2gh=(1+mM)v2⇒v=
⎷2gh1+mM hence option (A) is correct.
V=mMv=m√2gh√M(m+M) along - ve x -axis.
Hence option [B] is incorrect.
Since the location of center of mass does not change along the x-axis.
mΔxm/G+MΔxM/G=0 (x+1)2+(y+2)2=1 m(R−x)−Mx=0f
x=mRm+M ΔxM/G=−mRm+M
Hence option (D) is correct.
Δxm/G=R−x=MRM+m
Final position of m=−x=−mRm+M
Hence option (C) is incorrect.

Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS5videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - ASSERTION & REASON TYPE1videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE MAIN (ARCHIVE)53videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
Similar Questions
A block of mass m slides along a frictionless surface as shown in the figure. If it is releases from rest from A what is its speed at B?
 View Solution
View SolutionA block of mass 'm' is released on the top of a frictionless incline as shown in the figure. The time period of the oscillation of the block is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two blocks each of mass M are resting on a frictionless inclined plane as shown in fig then:
 AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
AThe block A moves down the planeBThe block B moves down the plane.CBoth the blocks remain at restDBoth the blocks move down the plane.
A block is lying on the horizontal frictionless surface. One end of a uniform rope is fixed to the block which is pulled in the horizontal direction by applying a force F at the other end. If the mass of the rope is half the mass of the block. The tension in the middle of the rope will be
View SolutionA small block slides with velocity 0.5√gr on the horizontal frictionless surface as shown in the figure. The block leaves the surface at point C . Calculate angle θ in the figure.
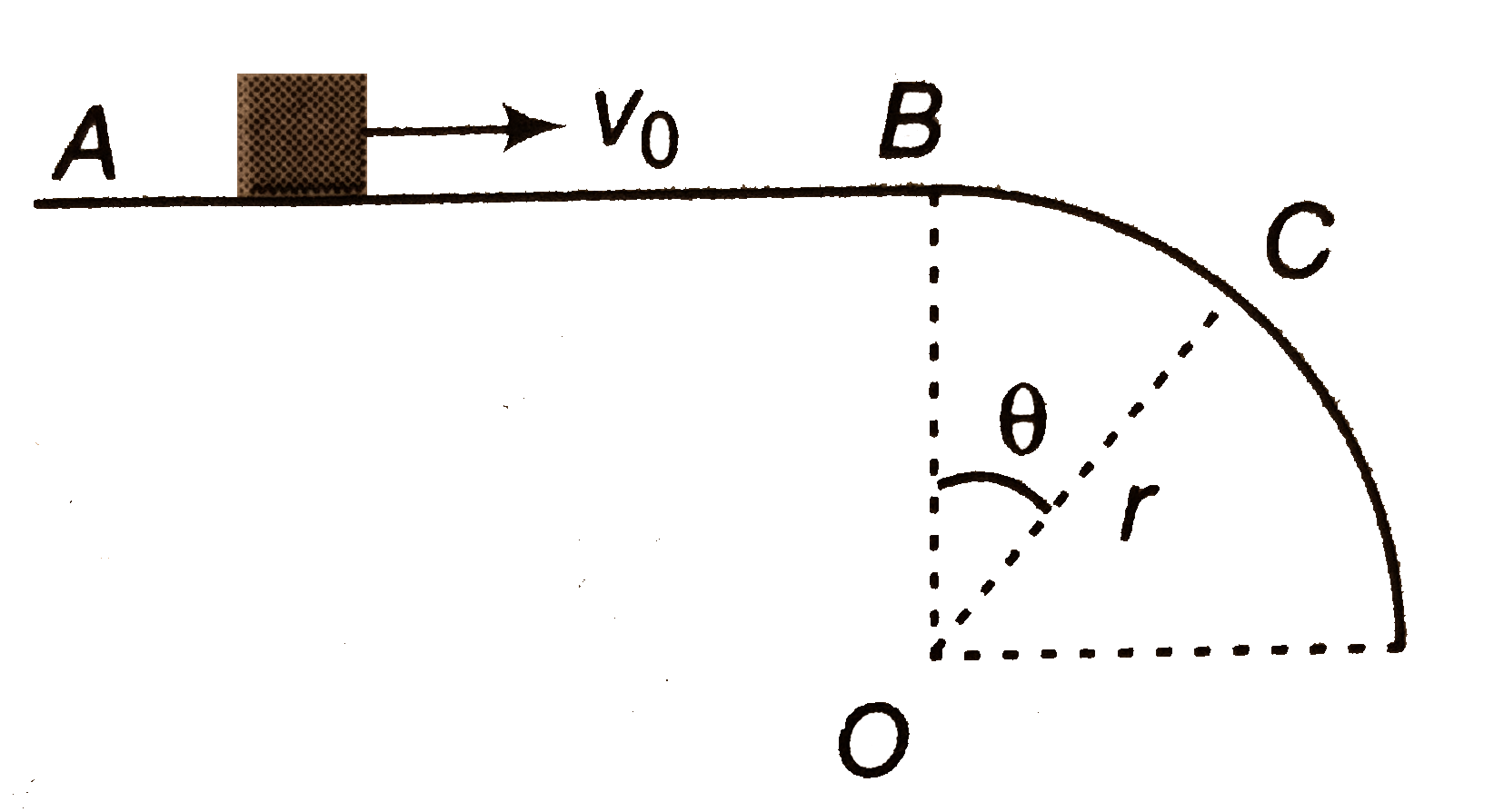 View Solution
View SolutionA block of mass m is released from a height R on the frictionless incline as shown. The incline leads to a circle of radius R/2. The maximum height attained by the block is
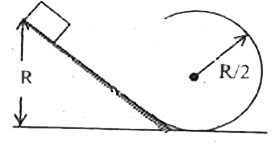 View Solution
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View SolutionTwo blocks, each having a mass M, rest on frictionless surfaces as shown in the figure. If the pulleys are light and frictionless and M on the incline is allowed to move down, then the tension in string will be
 View Solution
View SolutionA block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface.
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point
 View Solution
View Solution

