A wooden crate with a heavy machine weighing 3000 N slides on the ground when pushed by a lever AB of length 100 cm as shown in the figure. The force required to slide the crate acts at a distance of 10 cm from the fulcrum . If the coefficient of friction between the crate and the ground is $\sqrt{2}$ , find the effort required to move the crate. (Take the value of $\sqrt{2} = 1.4$ )

Text Solution

Verified by Experts

Different forces that act on the crate are shown in the figure

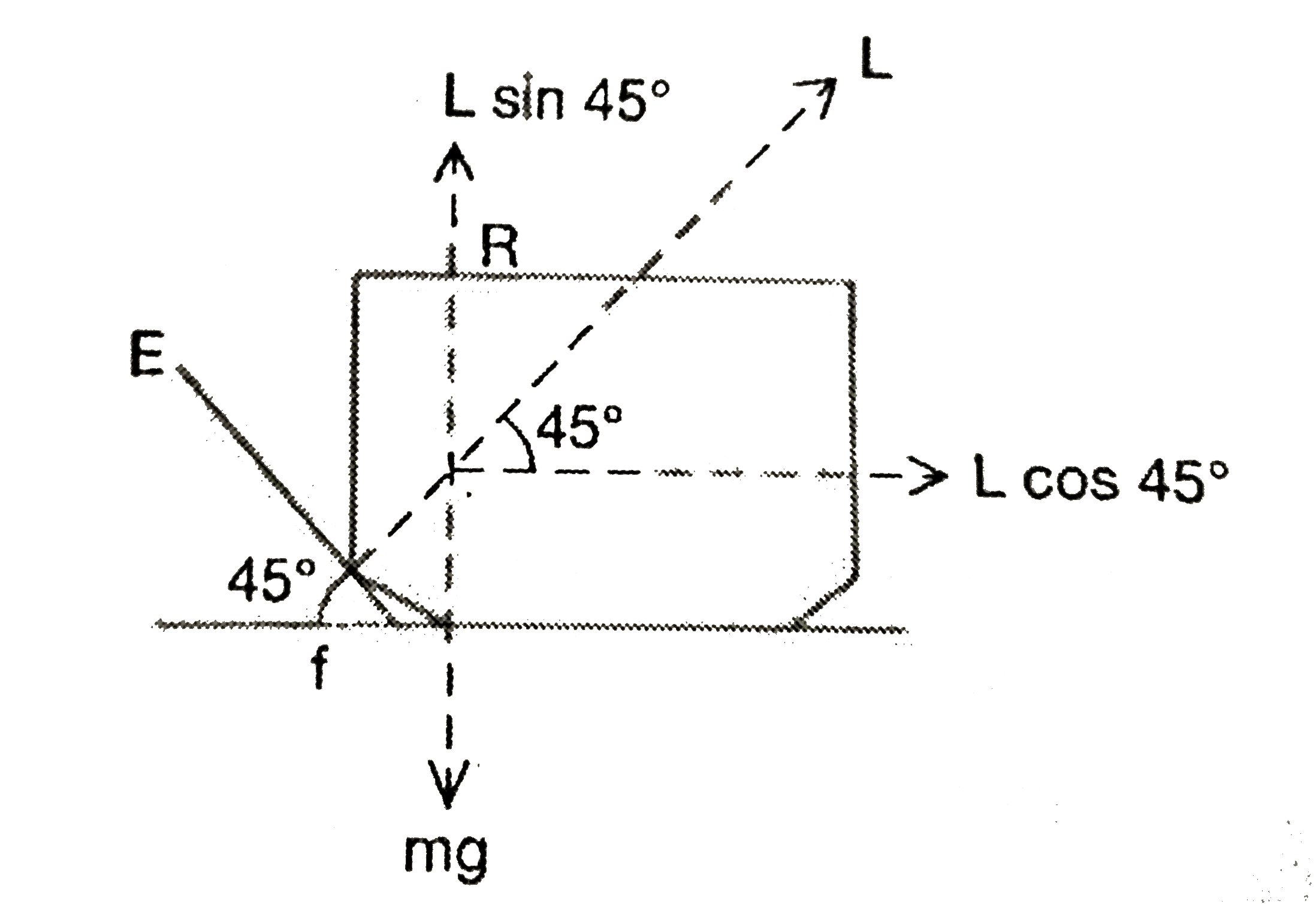
From the figure it is clear that
R + L sin 45 = mg
$R = [m g - \frac{L}{\sqrt{2}}]$ and the force that is responsible for the motion of the roller is L ${cos 45}^{\circ}$ .
Thus, $L {cos 45}^{\circ} = f = μ R \Rightarrow \frac{L}{\sqrt{2}} = μ (m g - \frac{L}{\sqrt{2}})$
$\frac{L}{\sqrt{2}} = μ m g . \frac{μ L}{\sqrt{2}} \Rightarrow \frac{L}{\sqrt{2}} (μ + 1) = μ m g$
Or $L = \frac{\sqrt{2} μ m g}{μ + 1}$
Now, (effort) (effort arm) = (load) (load arm)
Effort $= \frac{L \times l}{e} = \frac{l}{e} (\frac{\sqrt{2} μ m g}{μ + 1})$
Given $l = 100 c m, e = 100 c m$ ,
$m g = 3000 N$ and $μ = s q t (2)$
$= (\frac{10}{100}) (\frac{\sqrt{2} \times \sqrt{2} \times 3000}{\sqrt{2} + 1}) = 250 N$

Updated on:21/07/2023

In the above problem, the contact force between the man and the crate is
A2250N
B1125N
C750N
D375N
A man drags an m kg crate across a floor by pulling on a rope inclined at angle $θ$ above the horizontal. If the coefficient of static friction between the floor and crate is then the tension required in the rope to start the crate moving is :
A $\frac{μ_{s} m g}{(sin θ - μ_{s} cos θ)}$
B $\frac{μ_{s} m g}{(sin θ + μ_{s} cos θ)}$
C $\frac{μ_{s} m g}{(cos θ - μ_{s} sin θ)}$
D $\frac{μ_{s} m g}{(cos θ + μ_{s} sin θ)}$
If the coefficient of kinetic friction be in above question then the initial acceleration of the crate will be :
A $[(\frac{T}{m g}) (cos θ + μ_{k} sin θ) + μ_{k}] g$
B $[(\frac{T}{m g}) (cos θ + μ_{k} sin θ) - μ_{k}] g$
C $[(\frac{T}{m g}) (sin θ + μ_{k} sin θ) - μ_{k}] g$
D $[(\frac{T}{m g}) (sin θ + μ_{k} sin θ) + μ_{k}] g$