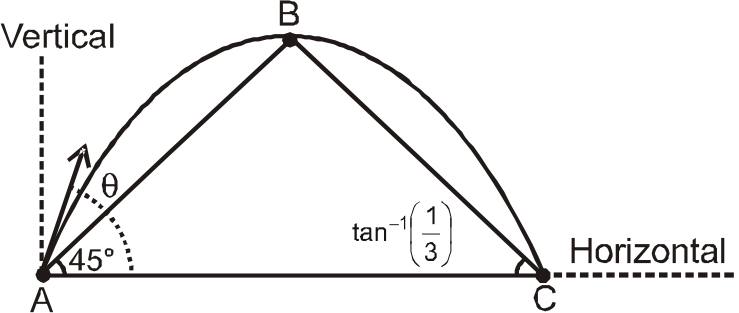
ABC is a triangle in vertical plane. Its two base angles ∠BAC and ∠BCA are 45∘ and tan−113 respectively. A particle is projected from point A such that is passes through vertices B and C. Angle of projectio is θ. Find the value of 3tanθ.

The correct Answer is:4
Step by step video, text & image solution for ABC is a triangle in vertical plane. Its two base angles /_BAC and /_BCA are 45^(@) and "tan"^(-1)1/3 respectively. A particle is projected from point A such that is passes through vertices B and C. Angle of projectio is theta. Find the value of 3 tan theta. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
ABC is a triangle in vertical plane. Its two base angles ∠BAC and ∠BCA are 45∘ and tan−1(1/3) respectively. A particle is projected from point A such that it passes through vertices B and C. Find angle of projection in degrees:
 A60∘B53∘Ctan−1(5/4)Dtan−1(5/3)
A60∘B53∘Ctan−1(5/4)Dtan−1(5/3)In a triangle ABC, right angled at C, find the value of tan A + tan B in terms of the sides a,b,c.
Aa2bcBa+bCb2acDc2abIf 1+tanθ1−tanθ=√3 , then find the value of θ.
A30∘B25∘C15∘D45∘
If θ is an acute angle and tanθ+secθ=1.5, find sinθ,tanθ and secθ.
View SolutionIn a triangle ABC if ∠A=θ and perpendiculars drawn from vertices B and C to respective opposite sides meet in P then find the value of ∠BPC in terms of θ.
View SolutionIf two angles of a triangle are tan−1(2)andtan−1(3), then find the third angles
View SolutionIf θ is a positive acute angle and tan2θtan3θ=1, then the value of (2cos25θ2−1) is
View SolutionΔABC is right angled at B.If m∠A=45∘,then find the value of (tanC+√32).
View Solution
