Ac cording to Stefan' law of radiation, a black body radiates energy σT4 from its unit surface area every second where T is the surface temperature of the black body and σ=5.67×10−8W/m2K4 is known as Stefan's constant. A nuclear weapon may be thought of as a ball of radius 0.5 m When detoneted, it reachs temperature of 106K and can be treated as a black body. (a) Estimate the power it radiates. (b) if surrounding has water at 30∘C how much water can 10% of the energy produced evaporate in 1s ? [sw=4186.0J/KgKandLυ=22.6×105J/kg] (c ) If all this energy U is in the form of radiation, corresponding momentum is p=U/c. How much momentum per unit time does it impart on unit area at a distance of 1 km ?
Let's solve the question step by step.
Given Data:
- Radius of the nuclear weapon (black body), r=0.5m
- Temperature, T=106K
- Stefan's constant, σ=5.67×10−8W/m2K4
- Specific heat of water, sw=4186.0J/kg K
- Latent heat of vaporization, Lv=22.6×105J/kg
- Surrounding water temperature, Tw=30∘C=303K
Part (a): Estimate the power it radiates.
1. Calculate the surface area of the black body:
A=4πr2=4π(0.5)2=4π(0.25)=πm2
2. Use Stefan's law to calculate the power radiated:
P=AσT4=π⋅(5.67×10−8)⋅(106)4
3. Calculate (106)4:
(106)4=1024
4. Substituting the values:
P=π⋅(5.67×10−8)⋅(1024)=π⋅5.67×1016≈1.78×1017W
Part (b): How much water can 10% of the energy produced evaporate in 1s?
1. Calculate 10% of the power:
E=0.1⋅P=0.1⋅(1.78×1017)=1.78×1016J
2. Calculate the temperature increase needed to reach boiling point (from 30°C to 100°C):
ΔT=100−30=70K
3. Using the formula for total heat:
E=mswΔT+mLv
Rearranging gives:
m=EswΔT+Lv
4. Substituting the values:
m=1.78×10164186⋅70+22.6×105
5. Calculating the denominator:
4186⋅70=292020J/kg
22.6×105=2260000J/kg
Total=292020+2260000=2552020J/kg
6. Calculating mass of water:
m=1.78×10162552020≈6976.5kg
Part (c): Calculate momentum imparted on unit area at a distance of 1 km.
1. Calculate the momentum p:
p=Uc=1.78×10173×108≈5.93×108kg m/s
2. Calculate the area at a distance of 1 km:
A=4πr2=4π(1000)2=4π⋅106m2
3. Calculate momentum per unit area:
Momentum per unit area=pA=5.93×1084π⋅106
4. Calculating the final value:
Momentum per unit area≈5.93×10812.566×106≈47.1N/m2
Summary of Results:
- (a) Power radiated: P≈1.78×1017W
- (b) Mass of water evaporated: m≈6976.5kg
- (c) Momentum per unit area at 1 km: ≈47.1N/m2
- Radius of the nuclear weapon (black body), r=0.5m
- Temperature, T=106K
- Stefan's constant, σ=5.67×10−8W/m2K4
- Specific heat of water, sw=4186.0J/kg K
- Latent heat of vaporization, Lv=22.6×105J/kg
- Surrounding water temperature, Tw=30∘C=303K
A=4πr2=4π(0.5)2=4π(0.25)=πm2
P=AσT4=π⋅(5.67×10−8)⋅(106)4
(106)4=1024
P=π⋅(5.67×10−8)⋅(1024)=π⋅5.67×1016≈1.78×1017W
E=0.1⋅P=0.1⋅(1.78×1017)=1.78×1016J
ΔT=100−30=70K
E=mswΔT+mLv
Rearranging gives:
m=EswΔT+Lv
m=1.78×10164186⋅70+22.6×105
4186⋅70=292020J/kg
22.6×105=2260000J/kg
Total=292020+2260000=2552020J/kg
m=1.78×10162552020≈6976.5kg
p=Uc=1.78×10173×108≈5.93×108kg m/s
A=4πr2=4π(1000)2=4π⋅106m2
Momentum per unit area=pA=5.93×1084π⋅106
Momentum per unit area≈5.93×10812.566×106≈47.1N/m2
- (a) Power radiated: P≈1.78×1017W
- (b) Mass of water evaporated: m≈6976.5kg
- (c) Momentum per unit area at 1 km: ≈47.1N/m2
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Very short Answer type Questions
15 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - Long answer type questions
12 Videos
- THERMODYNAMICS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - THERMODYNAMICS EXERCISE - LONG ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
Knowledge Check
If the temperature of hot black body is raised by 5%, rate of heat energy radiated would be increased by how much percentage ?
A12%B22%C32%D42%If the temperatures of a perfectly black body measured in Kelvin is doulbed, then the energy radiated per second becomes
Atwice the orginal valueB16 times the original valueChalf the original valueD4 times the original value
Gibbs-Helmoholtz equation relates the free energy change to the enthalpy and entropy changes of the process as
(ΔG)PT=ΔH−TΔS
The magnitude of ΔH does not change much with the change in temperature but the energy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
The dissolution of CaCl2.6H2O in a large volume of water is endothermic to the extent of 3.5kcalmol−1. For the reaction. CaCl2(s)+6H2O(l)→CaCl2.6H2O(s)ΔHis−23.2kcal. The heat of solution of anhydrous CaCI2 in large quantity of water will be
View SolutionA black body radiates energy at the rate of E W/m at a high temperature TK . When the temperature is reduced to T2K , the radiant energy will b
View SolutionIn the figure, the distribution of energy density of the radiation emitted by a black body at a given temperature is shown. The possible temperature of the black body is
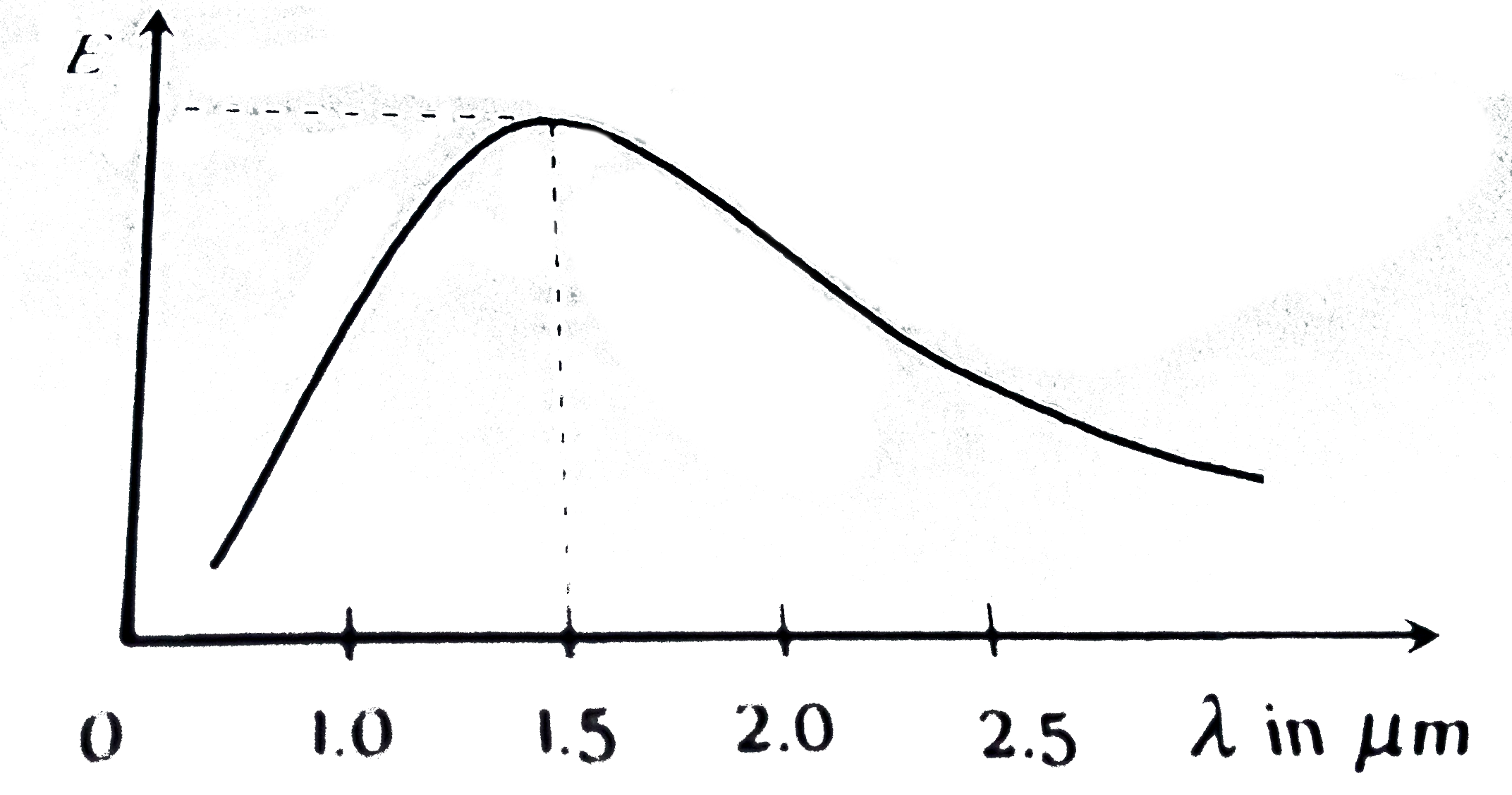
View SolutionCalculate the power of an incandescent lamp whose filament has a surface area of 0.19cm2 and is at a temperature of 3645K. Emmisivity of the surface is 0.4, σ=5.7×10−8Wm−2K−4 ?
View SolutionCalculate the temperature at which a perfect black body radiates at the rate of 1Wcm−2 , value of Stefan's constant,
σ=5.67×10−5Wm−2K−8
View SolutionA sphere of 8cm radius behaves like a black body. It is in thermal equilibrium with the surrounding and absorbs 10W of power radiated to it from surrounding. The temperature of the sphere (σ=5.67×10−8W/m2K4) is approximately.
View Solution
