According to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K, are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l. A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l. To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt.
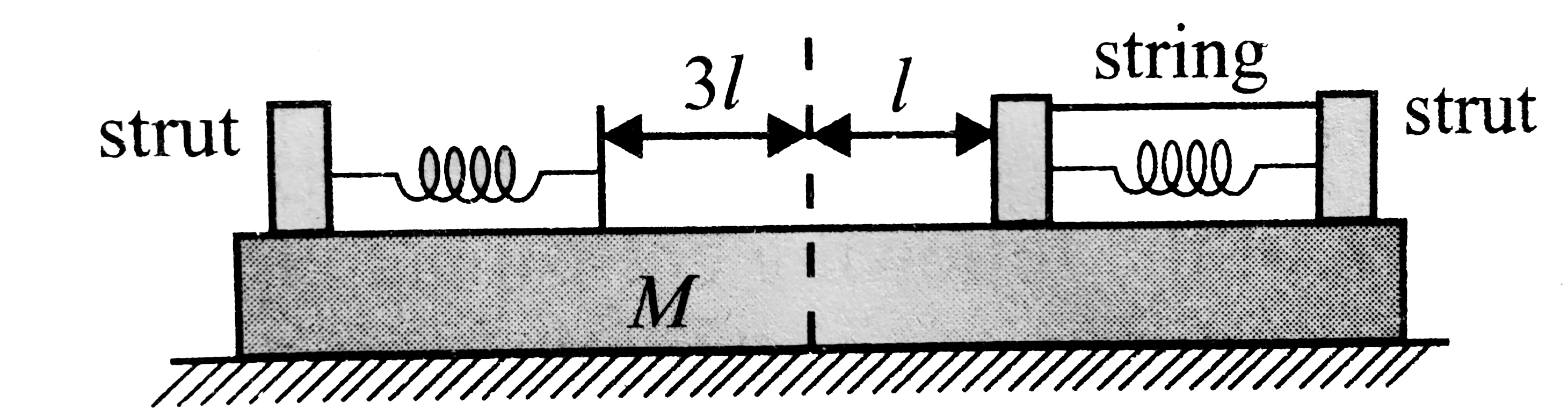
The maximum kinetic energy of the block m is
Kml22M(M+m)
Kml2M(M+m)
KMl22(M+m)
none of these
The correct Answer is:C
vm=Mm√KmM(M+M)l=√KMm(M=m)l
KE=12mv2m=KMl22(M+m)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Integer
16 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A bullet is fired on a fixed target. It penetrates inside the target through distance d=3.75cm and then stops. mass of the bullet is m=1kg and of the target is M=4kg. Now an identical bullet moving with the same velocity is fired on the identical target which is placed at rest on a frictionless horizontal surface. Then find the distance (in cm) to which the bullet will penetrate inside the target?
View SolutionA particle of mass 4 m which is at rest explodes into three fragments. Two of the fragments each of mass m are found to move with a speed v each in mutually perpendicular directions. The total energy released in the process of explosion is ............
View SolutionStatement I: In a two-body collision, the momenta of the particles are equal and opposite to one another, before as well as after the collision when measured in the centre of mass frame.
Statement. II: The momentum of the system is zero from the centre of mass frame.
View SolutionA colorimeter contains 400g of water at a temperature of 5∘C. Then, 200g of water at a temperature of +10∘C and 400g of ice at a temperature of −60∘C are added. What is the final temperature of the contents of calorimeter?
Specific heat capacity of water −1000 cal/kg/K
Specific latent heat of fusion of ice =80×1000 cal/kg
Relative specific heat of ice =0.5
View SolutionTo find the distance d over which a signal can be seen clearly in foggy conditions, a railways-engineer uses dimensions and assumes that the distance depends on the mass density ρ of the fog, intensity (power/area) S of the light from the signal and its frequency f. the engineer finds that d is proportional to S1/n. the value of n is
View SolutionAssertion: To conserve linear momentum of a system, no force should act on the system. Reason: If net force on a system is zero, its linear momentum should remain constant.
View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero. A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K , are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l . A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l . To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt. The maximum displacement of the plank is
View SolutionAccording to the principle of conservation of linear momentum if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain at rest in the absence of external force, that is, the displacement of centre of mass will be zero. A plank of mass M is placed on a smooth horizontal surface. light identical springs, each of stiffness K , are rigidly connected to struts at the end of the plank as shown in Fig. When the springs are in their unextended position, the distance between their free ends is 3l . A block of mass m is placed on the plank and pressed against one of the springs so that it is compressed to l . To keep the block at rest it is connected to the strut means of a light string. Initially, the system is at rest, Now the string is burnt. The maximum velocity of the plank is
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Find the relative velocity of the blocks after 'm' leaves contact with the spring.
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero. Two blocks of masses 'm' and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m' . Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest. What is the loss in the energy of the system due to breaking of B ?
View SolutionStatement-1 : Total linear momentum of system in centre of mass frame is zero only when there is no net external force. Statement-2 : Total linear momentum of system is conserved in absence of net external force.
View SolutionWill the momentum remain conserved if some external force acts on the system
View SolutionSuppose we define a quantity Linear Momentum as linear momentum =mass x speed.
The linear momentum of a system of particles is the sum of linear momentum of the individual particles. Can we state a principle of conservation of linear momentum as linear momentum of a system remains constant if no external force acts on it?
View SolutionWill the momentum remain conserved if some external force acts on the system ?
View SolutionShow that the total linear momentum of a system of particles is conserved in the absence of any external force. Also show that total linear momentum of the system is equal to the product of the total mass of the system and the velocity of its centre of mass.
View Solution
