Activate Windows Go to PC settings to activate Wine Show that the motion of a simple pendulum is simple harmonic and hence derive an equation for its time period. Find the length of a simple pendulum which ticks seconds. (g=9.8ms−2)
Text Solution
Simple pendulum : In a laboratory, a heavy metallic bob is suspended from a rigid support with the help of a spunless thread. This arrangement is known as simple pendulum
Let the length of simple pendulum is .l and the point of suspension is .S.. Let the pendulum is drawn to a side by a small angle θ and allowed free to oscillate in the vertical plane. Then It will oscillate between the extreme positions A and B with a displacement say .x. at any given time,
Let the bob is at one extreme position say B. The force vertically acting downwards is weight W =mg.
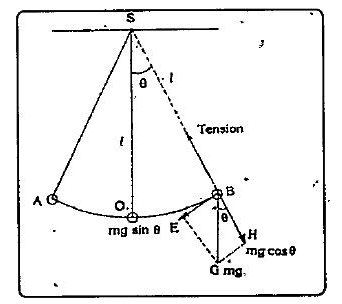
By resolving the weight into two perpendicular components
1) The component mg sin θ is responsible for the to and fro motion of the bob.
2) The component mg cos θ will balance the tension in the string.
Force useful for motion F = mg sin θ = ma ( From Newton.s 2nd Law )
∴a=gsinθ
When θ is small sin θ≈θ=arc radius =xl
∴a=g(x)l . . . . . . . (1) or a∝x
Since acceleration is proportional to displacement and ac celeration is always directed towards a fixed point the motion of simple pendulum is simple harmonic.
Time period of simple pendulum :
Time period of a body in S.H.M
2π√ya=2π√ displacement acceleration
From equation (1) a=gl× or xadisplacement (y)acceleration (a)=lg
∴ Time period of simple pendulum t=2π√ya=2π√lg
Problem :
In simple pendulum T=2π√lg or lgt24π2
For seconds pendulum T=2s⇒t2=4
∴l=9.8×44π2 = 1 m (∴π2≠arly9.8 )
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the length of a simple pendulum which ticks second?
A0.5 mB1 mC1.5 mD2 mThe time period of a simple pendulum of length 9.8 m is
A0.159 sB3.14 sC6.5 sD6.28 s
Show that the motion of simple pendulum is simple harmonic and hence derive an equation for its time period.What is Seconds pendulum?
View SolutionShow that for a small oscillations the motion of a simple pendulum is simple harmonic. Derive an expression of its time period.
View SolutionShow that for small oscillations the motion of a simple pendulum is simple harmonic. Derive an expression for its time period. Does it depend on the mass of the bob ?
View SolutionThe length of a simple pendulum is decreased by 21%. Find the percentage change in its time period.
View SolutionThe length of a simple pendulum is decreased by 21%. Find the percentage change in its time period.
View SolutionThe time period of a simple pendulum is 2 s. Find its frequency .
View Solution
