Aflat plate of area is separated from another large plate at rost by a liquid layer of uniform thickness . The tangential force needed to move the smaller plate with a constant velocity of i s 20 N. Calculate the coefficent of viscosity of the liquid.
The correct Answer is: Decapoise
To find the coefficient of viscosity of the liquid, we can use the relationship between the tangential force, the area of the plate, the velocity gradient, and the viscosity. The formula we will use is:
F=η⋅A⋅dvdx
Where:
- F = tangential force (in Newtons)
- η = coefficient of viscosity (in Pascal-seconds or N·s/m²)
- A = area of the plate (in m²)
- dvdx = velocity gradient (in s⁻¹)
Step 1: Write down the given values
- Area A=0.05m2
- Thickness dx=1μm=1×10−6m
- Velocity v=10cm/s=0.1m/s
- Tangential force F=20N
Step 2: Calculate the velocity gradient dvdx
The velocity gradient is defined as the change in velocity per unit distance. Since the plate is moving with a constant velocity, we can express the velocity gradient as:
dvdx=vdx
Substituting the values:
dvdx=0.1m/s1×10−6m=1×105s−1
Step 3: Rearrange the formula to solve for viscosity η
We can rearrange the original formula to solve for the coefficient of viscosity:
η=FA⋅dvdx
Step 4: Substitute the known values into the viscosity formula
Now, substitute the values into the equation:
η=20N0.05m2⋅1×105s−1
Step 5: Calculate the viscosity
Calculating the above expression:
η=200.05⋅1×105=205×103=205000=0.004N⋅s/m2
Step 6: Convert to decapoise
Since 1N⋅s/m2=10decapoise:
η=0.004N⋅s/m2=0.004×10decapoise=0.04decapoise
Final Answer
The coefficient of viscosity of the liquid is:
η=4×10−3decapoise
- F = tangential force (in Newtons)
- η = coefficient of viscosity (in Pascal-seconds or N·s/m²)
- A = area of the plate (in m²)
- dvdx = velocity gradient (in s⁻¹)
- Area A=0.05m2
- Thickness dx=1μm=1×10−6m
- Velocity v=10cm/s=0.1m/s
- Tangential force F=20N
The velocity gradient is defined as the change in velocity per unit distance. Since the plate is moving with a constant velocity, we can express the velocity gradient as:
We can rearrange the original formula to solve for the coefficient of viscosity:
Now, substitute the values into the equation:
Calculating the above expression:
Since 1N⋅s/m2=10decapoise:
The coefficient of viscosity of the liquid is:
Topper's Solved these Questions
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS (FROM POISEUILLE.S FORMULA)
19 Videos
- MOTION IN FLUIDS BOOK - ICSECHAPTER - MOTION IN FLUIDS EXERCISE - SELECTED PROBLEMS ( FROM PRESSURE, ARCHIMEDES. PRINCIPLE)
7 Videos
- INTERNAL ENERGY BOOK - ICSECHAPTER - INTERNAL ENERGY EXERCISE - SELECTED PROBLEMS (FROM HEAT ENGINES)
21 Videos
- OSCILLATIONS BOOK - ICSECHAPTER - OSCILLATIONS EXERCISE - SELECTED PROBLEMS (OSCILLATION IN A TUNNEL BORED THROUGH THE EARTH)
2 Videos
Similar Questions
A metal plate of area 103 cm2 rests on a layer o oil 6 mm thick. A tangential force of 10−2 N is appled on it to move it with a constant velocity of 6 cm s−1 . The coefficient of viscosity of the liquid is :-
View SolutionA metal square plate of 10cm side rests on 2mm thick caster oil layer. Calculate the horizontal force needed to move the plate with speed 3cms−1:( Coefficient of viscosity of caster oil is 15 poise. )
View SolutionA metal block of area 0.10 m2 is connected to a 0.02 kg mass via a string. The string passes over an ideal pulley (considered massless and frictionless) as shown in figure. A liquid with a flim of thickness 0.15 mm is placed between the plate and the table. When released the plate movees to the right with a constant speed of 0.075 m s−1. What is the coefficient of viscosity of the liquid?
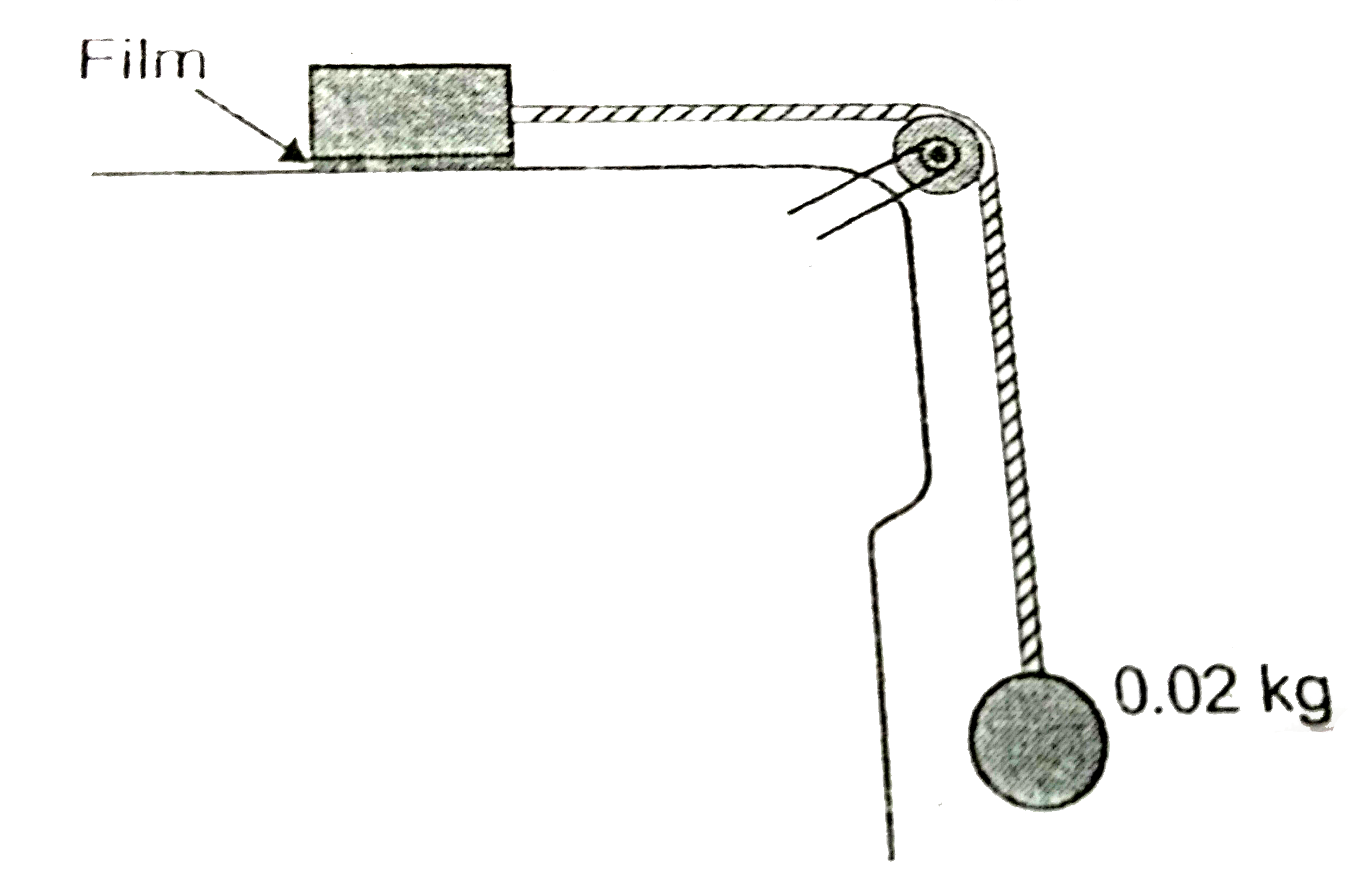
View SolutionA plate of area 100cm2 is placed on the upper surface of castor oil, 2mm thick. Taking the coefficient of viscosity to be 15.5 poise, calculate the horizontal force necessary to move the plate with a velocity 3cms−1.
View SolutionBetween a plate of area 100cm2 and another plate of area 100m2 there is a 1mm, thick layer of water, if the coefficient of viscosity of water is 0.01 poise, then the force required to move the smaller plate with a velocity 10cms−1 with reference to large plate is
View SolutionA lead sphere of 1.0mm diameter and relative density 11.20 attains a terminal velocity of 0.7cms−1 in a liquid of relative density 1.26.
Determine the coefficient of dynamic viscosity of the liquid.
View SolutionA metal plate 0.04m2 in area is lying on a liquid layer of thickness 10−3m and coefficient of viscosity 140 poise. Calculate the horizontal force needed to move the plate with a speed of 0.040 m/s.
View SolutionA metal plate of area 0.10m2 is connected to a 0.01kg mass via a string that passes over an ideal pulley (considered to be friction-less), as shown in the figure. A liquid with a film thickness of 3.0mm is placed between the plate and the table. When released the plate moves to the right with a constant speed of 0.085ms−1. Find the coefficient of viscosity of the liquid.

View SolutionA flat plate of area 0.1m2 is placed on a flat surface and is separated from it by a film of oil 10−5 m thick whose coefficielnt of .viscosity is 1.5Nsm−2 . The force required to cause the plate to slide on the surface at constant speed of 1mms−1is
View Solutionflat plate is separated from a large plate by a layer of glycerine of thickness 3×10−3m. If the coefficient of viscosity of glycerine is2Ns/m2 what is the force required to keep the plate moving with a velocity of6×10−2m/s. Area of the plate is 4.8×10−3m
View Solution
