All the edges of a block with parallel faces are unequal. Its longest edge is twice its shortest edge. The ratio of the maximum to minimum resistance between parallel faces is.
8
4
2
None of these
The correct Answer is:B
Let the length of varous edges in increasing order be l,x,2l, respectively.
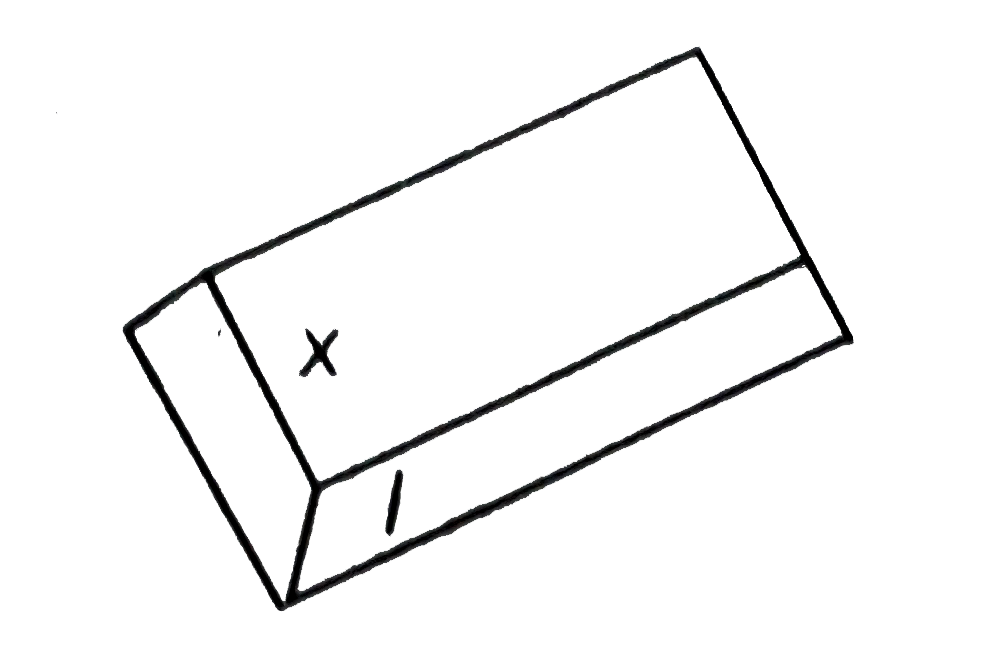
Maximumm resistance, Rmax=ρ2lxl=2ρx
and minimum resistance, Rmin=ρl2lx=ρ2x
∴ RmaxRmin=21/2=4
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE 2
26 Videos
- CURRENT ELECTRICITYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CURRENT ELECTRICITYEXERCISE - MHT CET CORNER
32 Videos
- CURRENT ELECTRICITYBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - CURRENT ELECTRICITYEXERCISE - MHT CET CORNER
32 Videos
- COMMUNICATION SYSTEMBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - COMMUNICATION SYSTEMEXERCISE - MHC CET Corner
6 Videos
- ELASTICITY BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - ELASTICITY EXERCISE - MHT CET CORNER
16 Videos
Similar Questions
All the edges of a block with parallel faces are unequal. Its longest edge is twice its shortest edge. The ratio of the maximum to minimum resistance between parallel faces is.
View SolutionThe edge of a cube is 4 cm . Find the ratio of its tota surface area to the area of its vertical faces.
View Solution
Knowledge Check
The sides of rectangular block are 2 cm, 3 cm ad 4 cm. The ratio of the maximum to minimum resistance between its parallel faces is
A3B4C2D1Comprehesion-I
Let k be the length of any edge of a regular tetrahedron (all edges are equal in length). The angle between a line and a plane is equal to the complement of the angle between the line and the normal to the plane whereas the angle between two plane is equal to the angle between the normals. Let O be the origin and A,B and C vertices with position vectors →a,→b and →c respectively of the regular tetrahedron.
The angle between any edge and a face not containing the edge isAcos−1(12)Bcos−1(14)Ccos−1(1√3Dcos−1(√32)Faces : The flat surface of any solid is called face.
Edges : Line segments where two faces meet is called an edge.
Vertices : Corners of the solid are its vertices.
Find the number of faces, edges and vertices respectively of rectangular prism.A6, 12, 10B6, 8, 10C4, 6, 8D6, 12, 8
A rectangular rigid fixed block has a long horizontal edge. A solid homogeneous cylinder of radus R is placed horizontally at rest its length parallel to the edge such that the exis of the cylinder and the endg of the block are in the same vertical plane as shown in the figure below. Ther is sufficinet friction present at the edge s that a very small displacement causes the cylinder to roll off the edge without slipping. Determine:

(a) the angle θc through which the cylinder rotates before it leaves contact with the edge,
(b) the speed of the centre of mass of the cylinder before leaving contact with the edge, and
(c) the ratio of the translational to rotational kinetic energy of the cylinder when its centre of mass is in horizontal line with the edge.
View SolutionTwelve identical resistances arranged on all edges of a cube. The resistors are all the same. Then find the equivalent resistance between the edges A and B as shown in.

View SolutionName the groups of all possible parallel edges of the box whose figure is shown below.
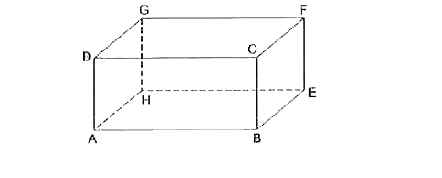
View SolutionIn Figure, name the face parallel to BFGC faces adjacent to BFGC three edges which meet in the vertex G.
View SolutionLet k be the length of any edge of a regular tetrahedron (a tetrahedron whose edges are equal in length is called a regular tetrahedron). Show that the angle between any edge and a face not containing the edge iscos−1(1/√3) .
View Solution
