An accumulator of emf 2V and negligible internal resistance is connected across a uniform wire of length 10 m and resistance 30Ω The appropriate terminals of a cell of emf 1.5V and internal resistance 1Ω is connected to one end of the wire and the other terminal of the cell is connected through a sensitive galvanometer to a slider on the wire. What is the length of the wire that will be required to produce zero deflection of the galvanometer? How will the balancing length change?
(a) When a coil of resistance 5Ω is placed in series with the accumulator.
(b) The cell of 1.5V is shunted with 5Ω resistor?
The correct Answer is:A, B
To solve the problem, we will analyze the circuit step by step and derive the necessary equations to find the balancing length of the wire that produces zero deflection in the galvanometer.
Step 1: Understanding the Circuit
We have:
- An accumulator (battery) with an EMF of 2V and negligible internal resistance connected across a uniform wire of length 10m and resistance 30Ω.
- A cell with an EMF of 1.5V and an internal resistance of 1Ω connected to one end of the wire, with the other terminal connected to a galvanometer and a slider on the wire.
Step 2: Finding the Total Resistance in the Circuit
The total resistance in the circuit when the cell is connected is the sum of the resistance of the wire and the internal resistance of the cell:
Rtotal=Rwire+Rinternal=30Ω+1Ω=31Ω
Step 3: Calculating the Current in the Circuit
Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=EaccumulatorRtotal=2V31Ω≈0.0645A
Step 4: Finding the Potential Drop Across the Wire
The potential drop across the wire can be calculated using Ohm's law:
Vwire=I×Rwire=0.0645A×30Ω≈1.935V
Step 5: Setting Up the Balancing Condition
At the balancing length x, the potential difference across the length of the wire is equal to the EMF of the cell:
VwireL⋅x=Ecell⟹1.935V10m⋅x=1.5V
Solving for x:
x=1.5V⋅10m1.935V≈7.75m
Step 6: Analyzing Changes in Balancing Length
(a) When a coil of resistance 5Ω is placed in series with the accumulator:
The new total resistance becomes:
Rnew total=30Ω+5Ω+1Ω=36Ω
Calculating the new current:
Inew=2V36Ω≈0.0556A
Calculating the new potential drop across the wire:
Vwire new=0.0556A×30Ω≈1.668V
Setting up the new balancing condition:
1.668V10m⋅x=1.5V⟹x=1.5V⋅10m1.668V≈8.98m
(b) When the cell of 1.5V is shunted with a 5Ω resistor:
The effective EMF of the shunted cell can be calculated using the formula for parallel resistors. The total resistance of the shunt is:
Rshunt=1Ω⋅5Ω1Ω+5Ω=56Ω
The new current through the circuit becomes:
Ishunt=2V30Ω+56Ω≈0.0667A
Calculating the new potential drop across the wire:
Vwire shunt=0.0667A×30Ω≈2.001V
Setting up the new balancing condition:
2.001V10m⋅x=1.5V⟹x=1.5V⋅10m2.001V≈7.49m
Summary of Results
1. The length of the wire required for zero deflection of the galvanometer is approximately 7.75m.
2. When a 5Ω coil is added in series, the balancing length changes to approximately 8.98m.
3. When the cell is shunted with a 5Ω resistor, the balancing length changes to approximately 7.49m.
We have:
- An accumulator (battery) with an EMF of 2V and negligible internal resistance connected across a uniform wire of length 10m and resistance 30Ω.
- A cell with an EMF of 1.5V and an internal resistance of 1Ω connected to one end of the wire, with the other terminal connected to a galvanometer and a slider on the wire.
The total resistance in the circuit when the cell is connected is the sum of the resistance of the wire and the internal resistance of the cell:
Rtotal=Rwire+Rinternal=30Ω+1Ω=31Ω
Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=EaccumulatorRtotal=2V31Ω≈0.0645A
The potential drop across the wire can be calculated using Ohm's law:
Vwire=I×Rwire=0.0645A×30Ω≈1.935V
At the balancing length x, the potential difference across the length of the wire is equal to the EMF of the cell:
VwireL⋅x=Ecell⟹1.935V10m⋅x=1.5V
Solving for x:
x=1.5V⋅10m1.935V≈7.75m
(a) When a coil of resistance 5Ω is placed in series with the accumulator:
The new total resistance becomes:
Rnew total=30Ω+5Ω+1Ω=36Ω
Calculating the new current:
Inew=2V36Ω≈0.0556A
Calculating the new potential drop across the wire:
Vwire new=0.0556A×30Ω≈1.668V
Setting up the new balancing condition:
1.668V10m⋅x=1.5V⟹x=1.5V⋅10m1.668V≈8.98m
The effective EMF of the shunted cell can be calculated using the formula for parallel resistors. The total resistance of the shunt is:
Rshunt=1Ω⋅5Ω1Ω+5Ω=56Ω
The new current through the circuit becomes:
Ishunt=2V30Ω+56Ω≈0.0667A
Calculating the new potential drop across the wire:
Vwire shunt=0.0667A×30Ω≈2.001V
Setting up the new balancing condition:
2.001V10m⋅x=1.5V⟹x=1.5V⋅10m2.001V≈7.49m
1. The length of the wire required for zero deflection of the galvanometer is approximately 7.75m.
2. When a 5Ω coil is added in series, the balancing length changes to approximately 8.98m.
3. When the cell is shunted with a 5Ω resistor, the balancing length changes to approximately 7.49m.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Example65videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point70videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Comprehension Example Type2videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Find the current drawn from a cell of emf 2 V and internal resistance 2Ω connected to the network given below.
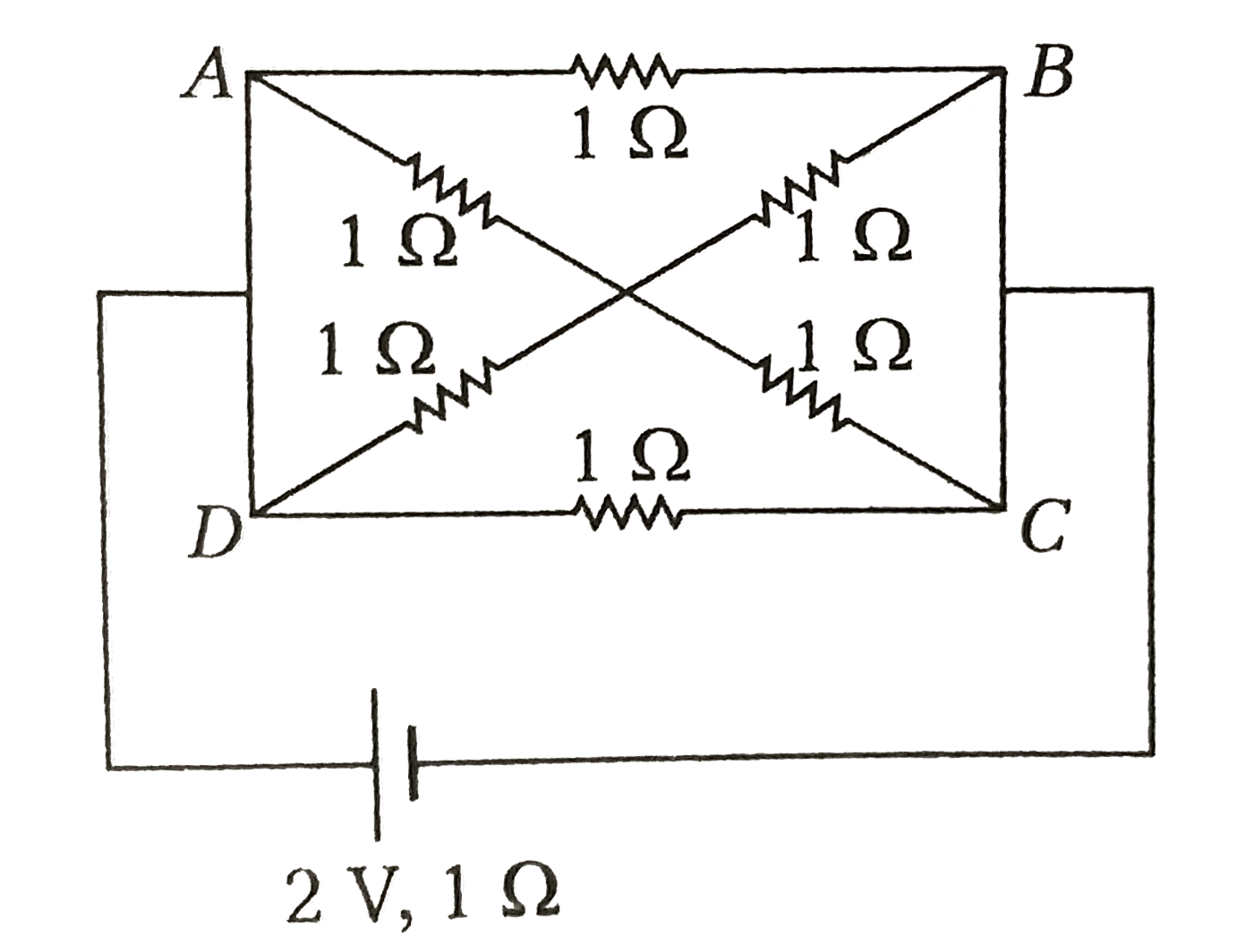 View Solution
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View SolutionA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
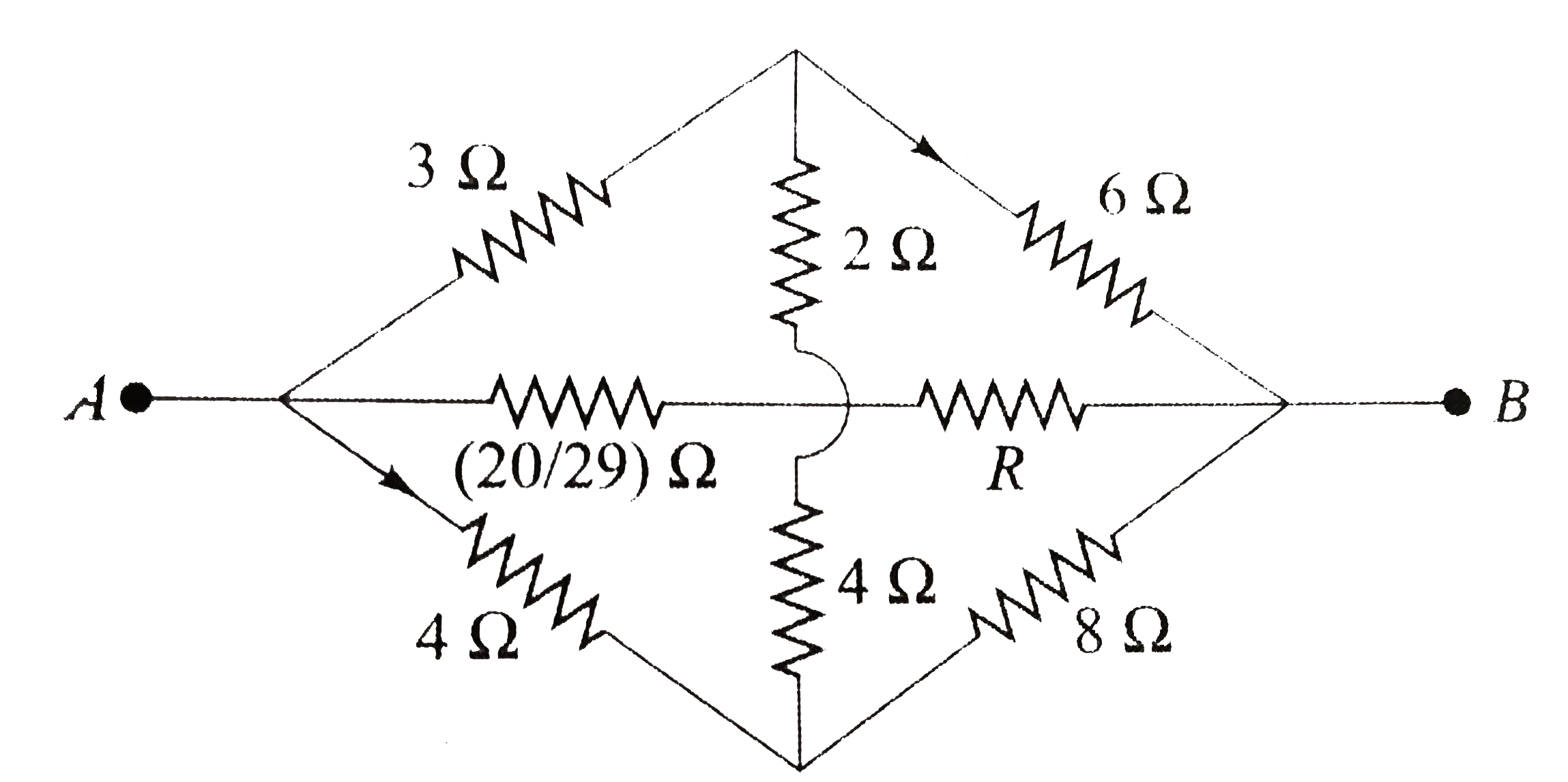 . View Solution
. View SolutionA cell whose e.m.f. is 2V and internal resistance is 0.1Ω is connected with a resistance of 3.9Ω the voltage across the cell terminal will be
View SolutionA battery of emf ε0=5V and internal resistance 5Ω is connected across a long uniform wire AB of length 1m and resistance per unit length 5Ωm−1. Two cells of ε1=1Vandε2=2V are connected as shown in the figure.
 View Solution
View SolutionEight cells marked 1 to 8, each of emf 5V and internal resistance 0.2Ω are connected as shown. What is the reading of ideal voltmeter ?
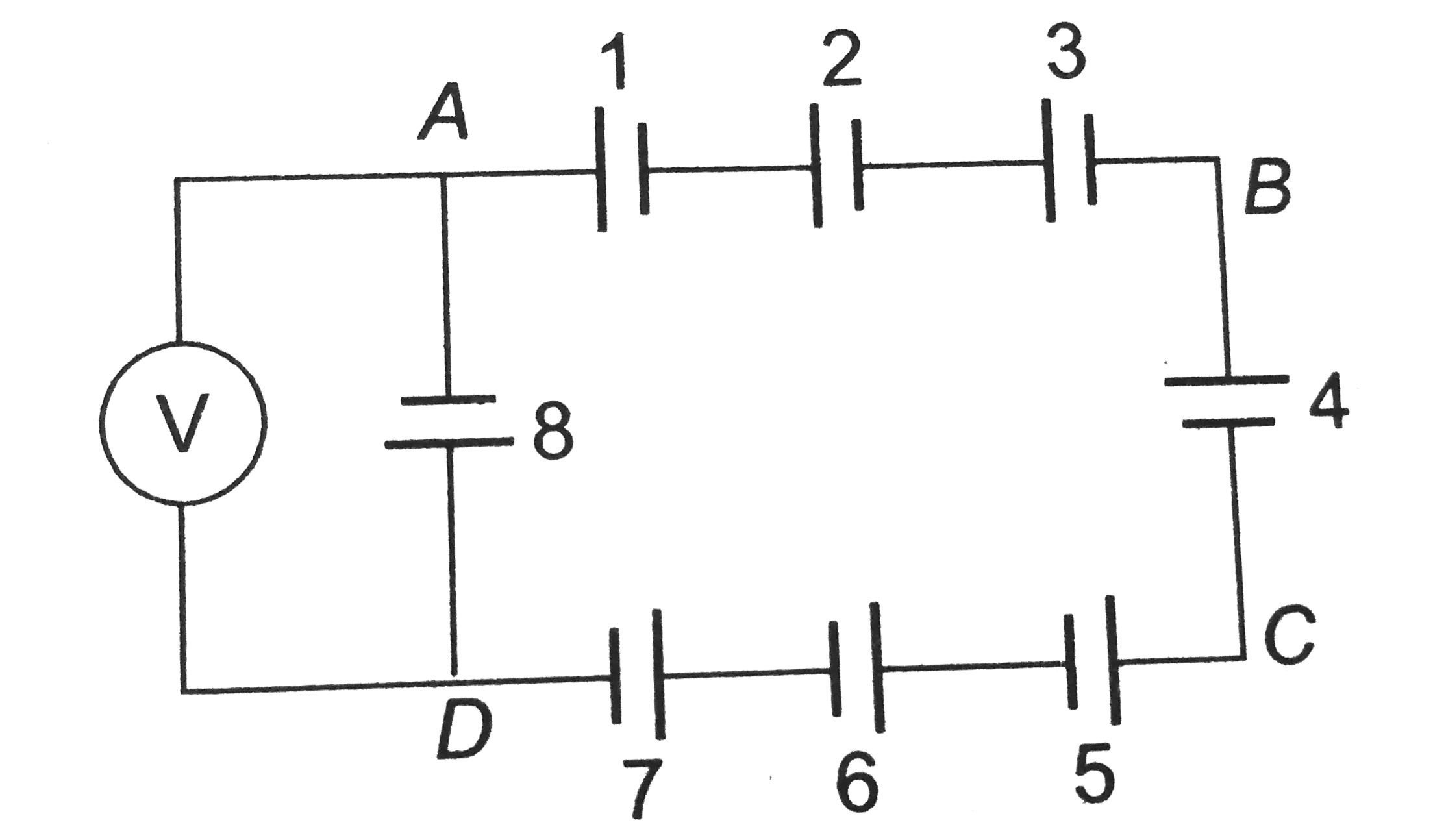 View Solution
View SolutionThe wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of e.m.f. 2V and internal resistance 1Ω. The current flowing through the potentiometer wire is
View SolutionA voltmeter of resistance 998Ω is connected across a cell of emf 2 V and internal resistance 2Ω. Find the p.d. across the voltmeter, that across the terminals of the cell and percentage error in the reading of the voltmeter.
View SolutionA thin uniform wire AB of length 50 cm and resistance 1Ω is connected to be terminals of a battery of emf ε1=2.2V and internal resistance 0.1Ω. If the terminals of another cell (assume ideal) are connected to two points 25 cm apart on the wire AB without altering the current in the wire AB, the emf ε2 of cell in volts is :
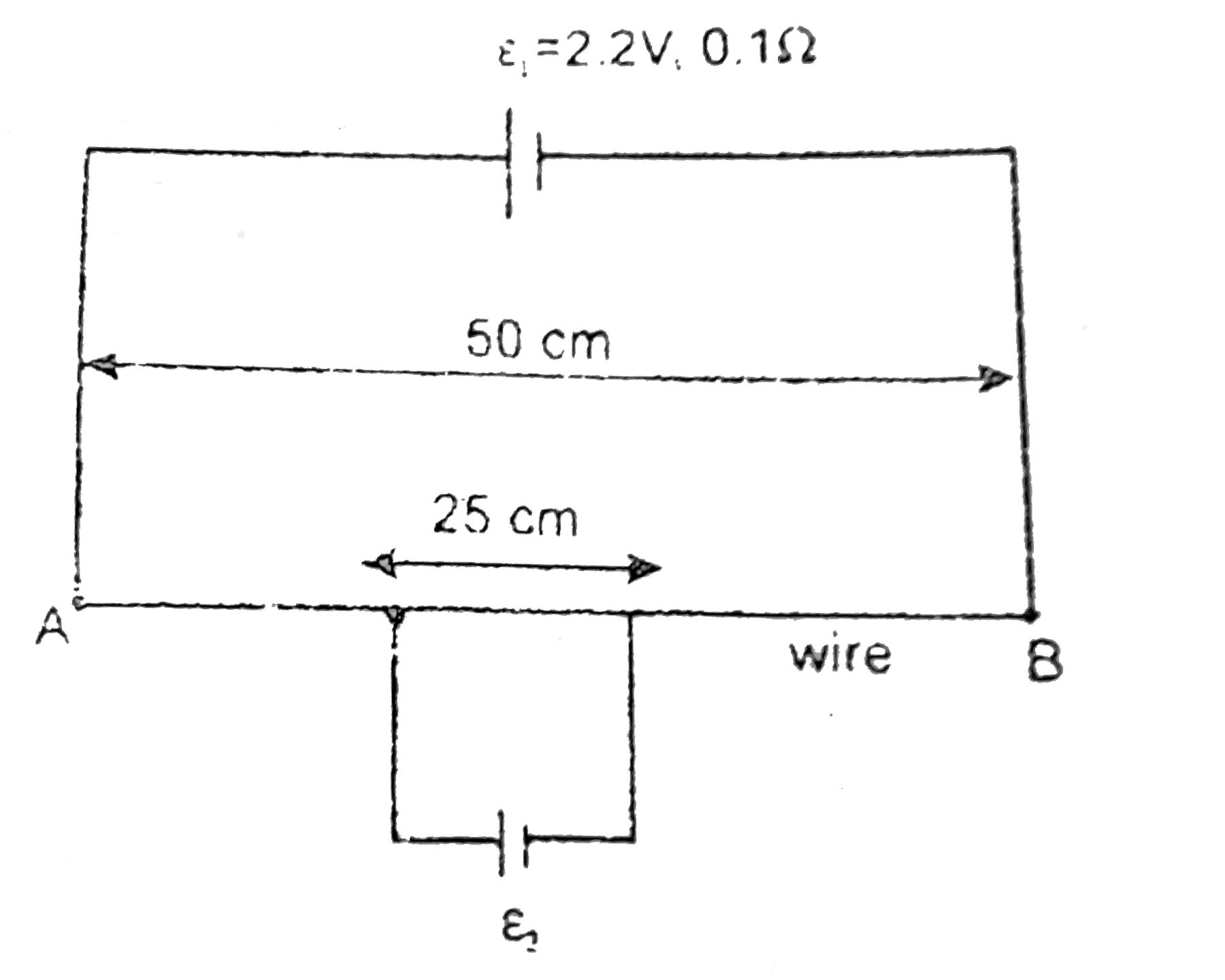 View Solution
View SolutionA 6V battery of internal resistance 1Ω is connected across a uniform wire AB of length 100 cm. The positive terminal of another battery of E.M.F 4V and internal resistance 1Ω is joined to the point A as shown. The distance of point P from A is α×10cm. Find the value of α, for which there is no current through the galvanometer. (resistance of AB wire is 5Ω)
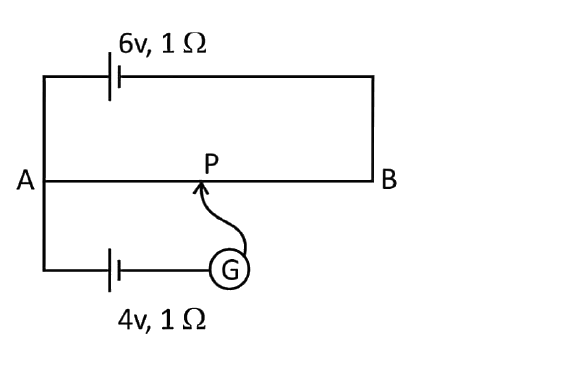 View Solution
View Solution

