An aeroplane has to go from a point A to another point B, 500km away due 30∘ east of north. Wind is blowing due north at a speed of 20m/s. The steering-speed of the plane is 150m/s. (a) Find the direction in which the pilot should head the plane to reach the point B. (b) Find the time taken by the plane to go fram A to B.
The correct Answer is:A, B
IN resultant direction →R, the plane reaches the point B.
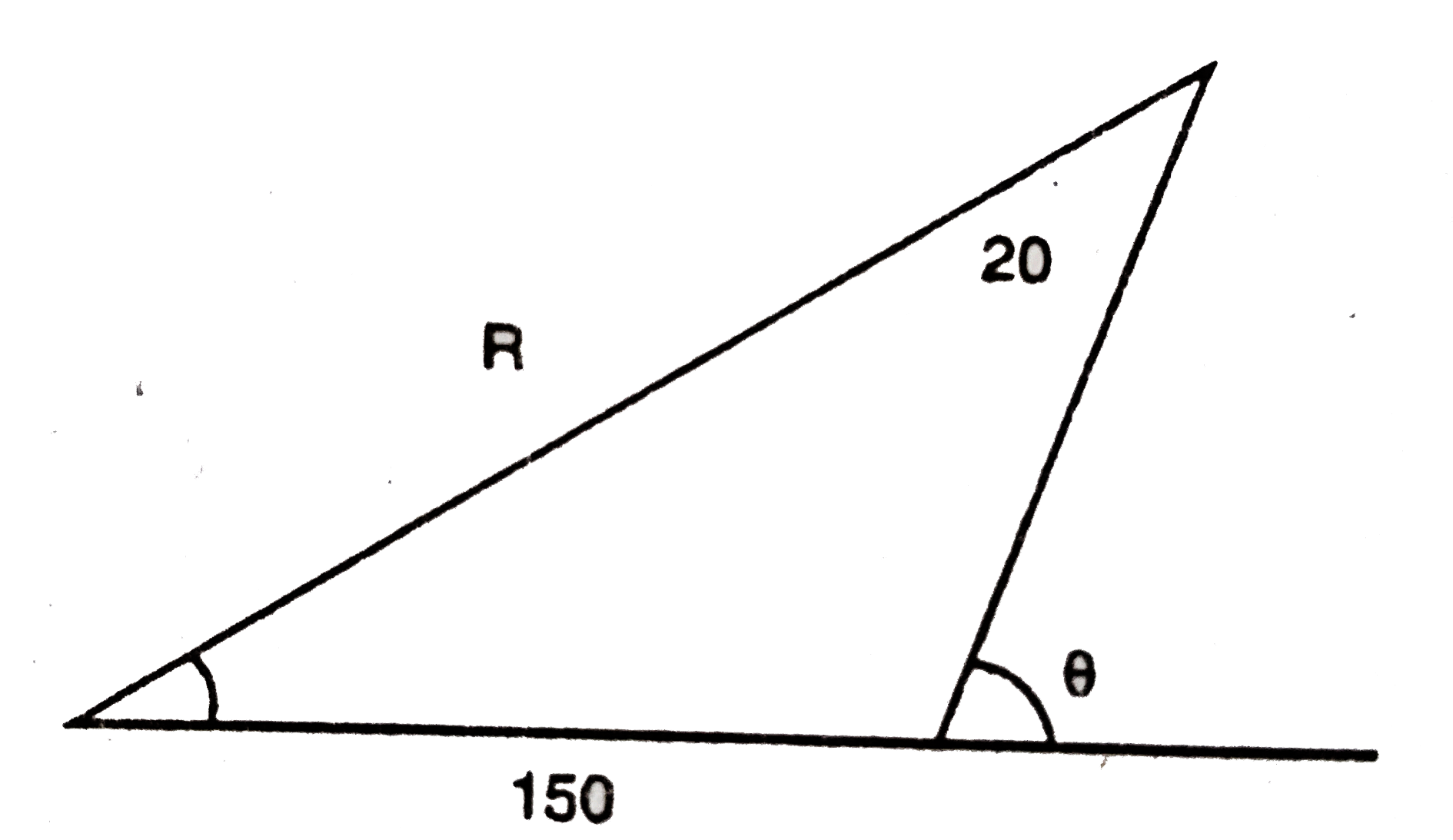
Velocityofw∈g,→Vm=20ms
Velocityofaeropla≠,Va=150ms
In △ACD, according to sine formula
∴20siNA=150sin300
→sinA=20150sin300
=20150×2=115
→A=sin−1(115)
→A=sin−1(115)
a The direction is sin−1(115) east of the line AB.
b. sin−1115=3048'
→00+3048'=33048'<br>R=sqrt(150+20+2(150)20 cos (33^0 48'))<br> = sqrt(27886) = 167 m/s<br> time = S/v = 500000/167<br> = 2994 sec = 49.0 ~~ 50 min.
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Objective 210videos
REST AND MOTION : KINEMATICS
- BOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Exercises34videos
PHYSICS AND MATHEMATICS
- BOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises86videos
ROTATIONAL MECHANICS
Similar Questions
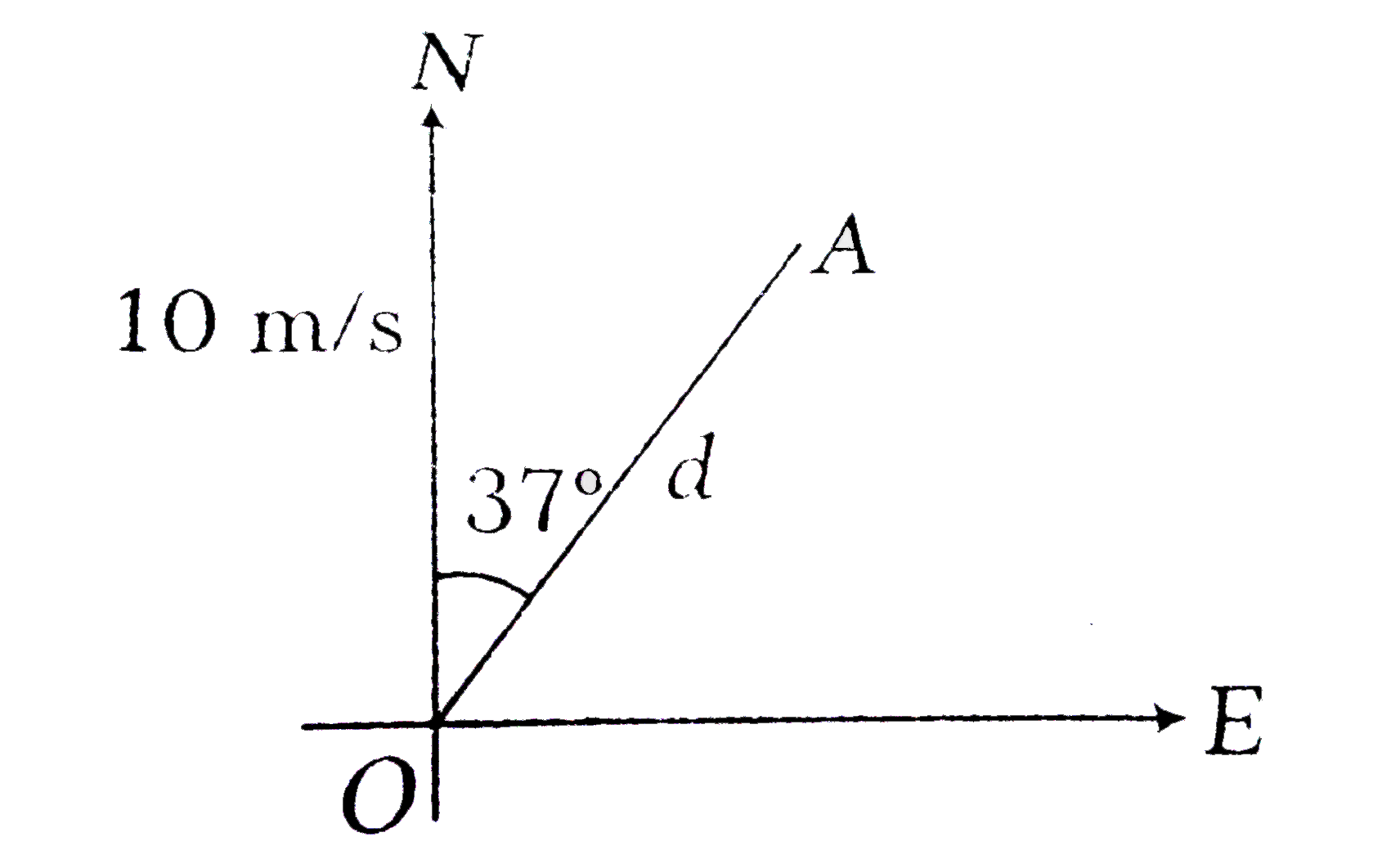
An aeroplane has to go from a point O to another point A, at distance d due 37∘ east of north. A wind is blowing due north at a speed of 20m/s. The air speed of the plane is v. (a) Find the direction in whihc the pilot should head the plane to reach the point A. (b) Find the time taken by the plane to go from O to A.
View SolutionAn aeroplane has to go from a point P to another point Q, 1000 km away due north. Wind is blowing due east at a speed of 200km/h. The air speed of plane is 500km/h.
(a) Find the direction in which the pilot should head the plane to reach the point Q.
(b) Find the time taken by the plane to go from P to Q.View Solution
Knowledge Check
- Question 1 - Select One
A ship is travelling due east at 10 km/h. A ship heading 30∘ east of north is always due north from the first ship. The speed of the second ship in km/h is
A20√2B20√3/2C20D20/√2 - Question 2 - Select One
To go from town A to town B a plane must fly about 1780 km at an angle of 30∘ west of north. How far West of A is B?
A1542kmB1452kmC1254kmD890 km
An aeroplane has to go from a point O to another point A, at distance d due 37∘ East of North. A wind is blowing due North at a speed of 10ms−1. The air speed of the plane is v. (i) Find the direction in which the pilot should head the plane to reach the point A. (ii) Find the time taken by the plane to go from O to A.
 View Solution
View SolutionTo go from town A to town B a plane must fly about 1780km at an angle of 30∘ west of north.How far north of A is B? is
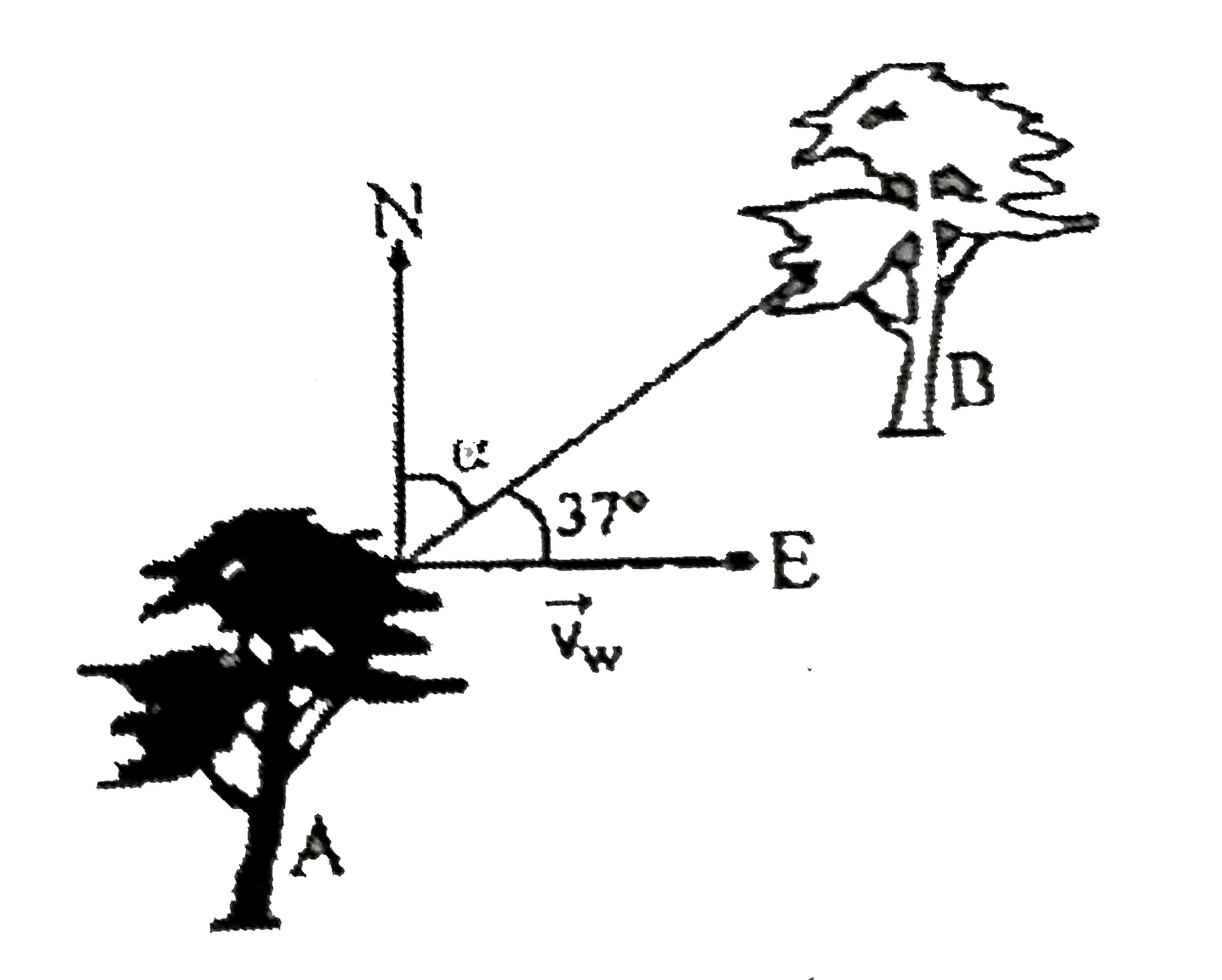
View SolutionWind is blowing in the east direction with a speed of 2m/s. A,. bird wishes to travel from tree A to tree B. Tree B is 100 m · away from A in a direction 37∘ north of east the velocity of ·bird in still air is 4 m/s.
( a) Find the direction in which bird should fly so that it can reach from A to B directly.
(b) Find the actual velocity of the bird during the flight.
(c) Find the time taken by the bird to reach B.
 View Solution
View SolutionVelocity of the boat with respect to river is 10 m/s. From point A it is steered in the direction shown to reach point C. Find the time of the trip and distance between B and C
 View Solution
View SolutionIf a train, A, 250 m long , travelling at a speed of 20 m/s takes 30 s to overtake another train B travelling at a speed of 18 km/h in the same direction. then find the length of the train B.
View SolutionAn aeroplane pilot wishes to fly due west A wind of 100kmh−1 is blowing towards south.
(a) If the speed of the plane (its speed in still air) is 300kmh−1 in which direction should the pilot head ?
(b) What is the speed of the plane with respect tom ground ? Illustrate with a vector diagram.View Solution

