An earth satellite is revolving in a circular orbit of radius a with velocity υ0. A gun in the satellite is aimed directly towards the earth. A bullet is fired from the gun with muzzle velocity υ02. Neglecting resistance offered by cosmic dust and recoil of gun, calculate maximum and minimum distance of bullet from the center of earth during its subsequent motion.
Orbital speed of satellite is
υ0=√GMa ..(i)
From conservation of angular momentum at P and Q, we have
maυ0=mυr
or υ=aυ0r ..(ii)
From conservation of mechanical energy at P and Q, we have
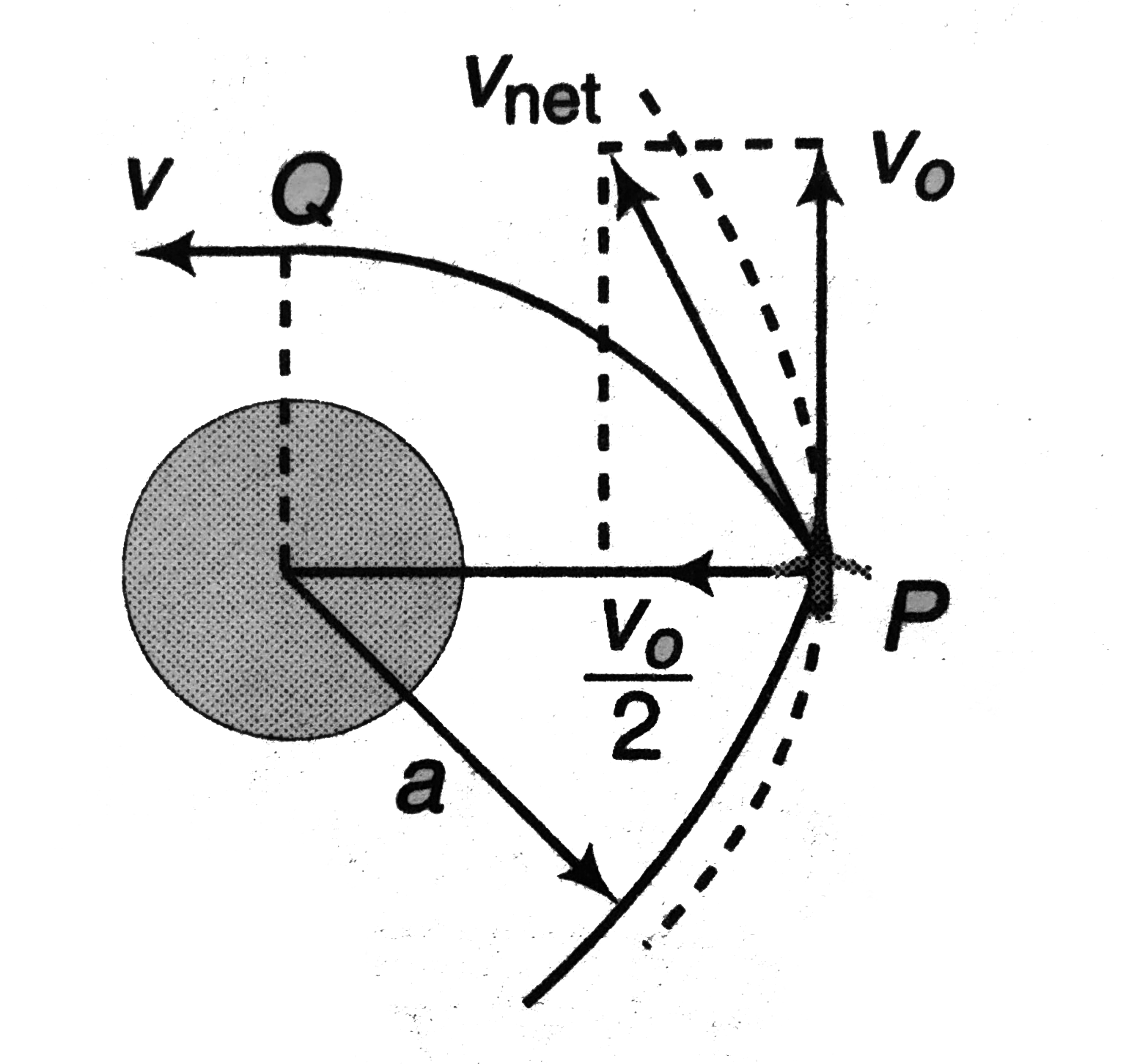
12m(υ20+υ204)−GMma=12mυ2−GMmr
or 58υ20−GMa=υ22−GMr
Subsituting value of υ and υ0 Eqs. (i) and (ii), we get
58GMa−GMa=a2r2.(GM2a)−GMr
or −38a=a2r2−1r
or −3r2=4a2−8ar
or 3r2−8ar+4a2=0
or r=8a±√64a2−48a26
or r=8a±4a6
or r=2a and 2a3
Hence, the maximum and minimun distances are 2a nad 2a3 respectively.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.15videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.29videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Solved Examples16videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
A satellite is revolving round the earth in a circular orbit of radius r and velocity υ0. A particle is projected from the satellite in forward direction with realative velocity υ=(√5/4−1)υ0. Calculate its minimum and maximum distances from earth's centre during subsequent motion of the particle.
View SolutionA satellite is revolving near by earth of radius =Re. If its velocity is increased √32v where v is the orbital speed of satellite then find maximum distance of satellite from the center of the earth.
View SolutionAn artificial satellite is moving in a circular orbit around the earth with a speed equal to half the escape velocity from the earth of radius R. The height of the satellite above the surface of the earth is
View SolutionA satellite is revolving round the earth in a circular orbit with a velocity of 8km/s. at a height where acceleration due to gravity is 8m/s2. How high is the satellite from the earth ? (Take R = 6000 km)
View SolutionAn artificial satellite is revolving in a circular orbit at a height of 1200 km above the surface of the earth. If the radius of the earth is 6400 km, mass is 6×1024kg find the orbital velocity
(G=6.67×10−11Nm2/kg2)View SolutionA satellite is orbiting around the earth in a circular orbit of radius r. A particle of mass m is projected from the satellite in a forward direction with a velocity v=2/3 times the orbital velocity (this velocity is given w.r.t. earth). During subsequent motion of the particle, its minimum distance from the centre of earth is
View SolutionIf the earth were to spin faster, acceleration due to gravity at the poles :
View SolutionA satelite is revolving in a circular orbit at a height h above the surface of the earth of radius R. The speed of the satellite in its orbit is one-fourth the escape velocity from the surface of the earth. The relation between h and R is
View SolutionA projectile is fired from the surface of earth of radius R with a velocity kυe (where υe is the escape velocity from surface of earth and k<1). Neglecting air resistance, the maximum height of rise from centre of earth is
View SolutionA planet A moves along an elliptical orbit around the Sun. At the moment when it was at the distance r0 from the Sun its velocity was equal to v0 and the angle between the radius vector r0 and the velocity vector v0 was equal to α. Find the maximum and minimum distances that will separate this planet from the Sun during its orbital motion.
View Solution

