Three particles, each of the mass m are situated at the vertices of an equilateral triangle of side a. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation a. Find the initial velocity that should be given to each particle and also the time period of the circular motion. (F=Gm1m2r2)
The correct Answer is:A
To solve the problem of three particles each of mass m situated at the vertices of an equilateral triangle of side a, we need to find the initial velocity that should be given to each particle and the time period of their circular motion.
1. Understanding the Configuration:
- We have three particles (m1, m2, m3) each of mass m located at the vertices of an equilateral triangle with side length a. The angle between any two sides of the triangle is 60 degrees.
2. Finding the Radius of Circular Motion:
- The center of the circle in which the particles will move lies at a distance from each vertex. This distance can be calculated as follows:
- The distance from a vertex to the center of the triangle (circumcenter) is given by \( r = \frac{a}{\sqrt{3}} \).
3. Calculating the Gravitational Force:
- The gravitational force between any two particles is given by the formula:
\(
F = \frac{G m^2}{a^2}
\)
- Since there are two forces acting on each particle due to the other two particles, we need to find the net force acting on one particle.
4. Finding the Net Force:
- The two gravitational forces acting on a particle from the other two particles can be resolved into components. The net force \( F_{net} \) can be calculated using the formula for the resultant of two forces at an angle:
\(
F_{net} = \sqrt{F^2 + F^2 + 2F \cdot F \cdot \cos(60^\circ)} = \sqrt{2F^2 + 2F^2 \cdot \frac{1}{2}} = \sqrt{3F^2} = \sqrt{3}F
\)
- Substituting for \( F \):
\(
F_{net} = \sqrt{3} \cdot \frac{G m^2}{a^2}
\)
5. Equating to Centripetal Force:
- The net gravitational force provides the centripetal force required for circular motion:
\(
F_{net} = \frac{m v^2}{r}
\)
- Substituting for \( r \):
\(
\sqrt{3} \cdot \frac{G m^2}{a^2} = \frac{m v^2}{\frac{a}{\sqrt{3}}}
\)
- Rearranging gives:
\(
v^2 = \frac{\sqrt{3} G m^2}{a^2} \cdot \frac{a}{\sqrt{3}} = \frac{G m}{a}
\)
- Therefore, the initial velocity \( v \) is:
\(
v = \sqrt{\frac{G m}{a}}
\)
6. Finding the Time Period:
- The time period \( T \) of circular motion can be calculated using the formula:
\(
T = \frac{2 \pi r}{v}
\)
- Substituting for \( r \) and \( v \):
\(
T = \frac{2 \pi \cdot \frac{a}{\sqrt{3}}}{\sqrt{\frac{G m}{a}}}
\)
- Simplifying gives:
\(
T = \frac{2 \pi a}{\sqrt{3}} \cdot \sqrt{\frac{a}{G m}} = \frac{2 \pi a^{3/2}}{\sqrt{3 G m}}
\)
Final Answers:
- The initial velocity \( v \) that should be given to each particle is:
\(
v = \sqrt{\frac{G m}{a}}
\)
- The time period \( T \) of the circular motion is:
\(
T = \frac{2 \pi a^{3/2}}{\sqrt{3 G m}}
\)
- We have three particles (m1, m2, m3) each of mass m located at the vertices of an equilateral triangle with side length a. The angle between any two sides of the triangle is 60 degrees.
- The center of the circle in which the particles will move lies at a distance from each vertex. This distance can be calculated as follows:
- The distance from a vertex to the center of the triangle (circumcenter) is given by \( r = \frac{a}{\sqrt{3}} \).
- The gravitational force between any two particles is given by the formula:
\(
F = \frac{G m^2}{a^2}
\)
- Since there are two forces acting on each particle due to the other two particles, we need to find the net force acting on one particle.
- The two gravitational forces acting on a particle from the other two particles can be resolved into components. The net force \( F_{net} \) can be calculated using the formula for the resultant of two forces at an angle:
\(
F_{net} = \sqrt{F^2 + F^2 + 2F \cdot F \cdot \cos(60^\circ)} = \sqrt{2F^2 + 2F^2 \cdot \frac{1}{2}} = \sqrt{3F^2} = \sqrt{3}F
\)
- Substituting for \( F \):
\(
F_{net} = \sqrt{3} \cdot \frac{G m^2}{a^2}
\)
- The net gravitational force provides the centripetal force required for circular motion:
\(
F_{net} = \frac{m v^2}{r}
\)
- Substituting for \( r \):
\(
\sqrt{3} \cdot \frac{G m^2}{a^2} = \frac{m v^2}{\frac{a}{\sqrt{3}}}
\)
- Rearranging gives:
\(
v^2 = \frac{\sqrt{3} G m^2}{a^2} \cdot \frac{a}{\sqrt{3}} = \frac{G m}{a}
\)
- Therefore, the initial velocity \( v \) is:
\(
v = \sqrt{\frac{G m}{a}}
\)
- The time period \( T \) of circular motion can be calculated using the formula:
\(
T = \frac{2 \pi r}{v}
\)
- Substituting for \( r \) and \( v \):
\(
T = \frac{2 \pi \cdot \frac{a}{\sqrt{3}}}{\sqrt{\frac{G m}{a}}}
\)
- Simplifying gives:
\(
T = \frac{2 \pi a}{\sqrt{3}} \cdot \sqrt{\frac{a}{G m}} = \frac{2 \pi a^{3/2}}{\sqrt{3 G m}}
\)
- The initial velocity \( v \) that should be given to each particle is:
\(
v = \sqrt{\frac{G m}{a}}
\)
- The time period \( T \) of the circular motion is:
\(
T = \frac{2 \pi a^{3/2}}{\sqrt{3 G m}}
\)
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:Miscellaneous Examples
Explore 8 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:Exercise 13.1
Explore 5 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
Three particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.

The gravitational potential at O is
View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View Solution
Knowledge Check
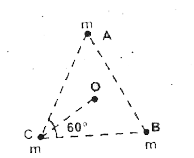
Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2
Three particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
Force acting on particle C, due to particle A and B
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionThree equal masses of 1.5 kg each are fixed at the vertices of an equilateral triangle of side 1 m. What is the force acting on a particle of mass 1 kg placed at its centroid ?
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L as shown in the figure. Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
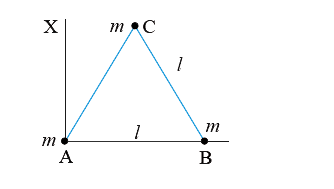
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View Solution