An electron falls from rest through a vertical distance h in a uniform and vertically upward directed electric field E. the direction of electric field is now reversed, keeping its magnitude the same. A proton is allowed to fall from rest in it through the same vertical distance h.The time of fall of the electron, in comparison to the time of flal of the proton is
10 times greater
5 times greater
smaller
equal
The correct Answer is:C
To solve the problem, we need to analyze the motion of an electron and a proton falling through the same vertical distance h in an electric field E. Let's break down the solution step by step.
Step 1: Understand the Forces Acting on the Electron and Proton
- The force acting on the electron (Fe) in the upward electric field is given by:
Fe=−eE
where e is the charge of the electron (approximately 1.6×10−19C).
- The force acting on the proton (Fp) when the electric field is reversed (downward) is:
Fp=eE
where e is the charge of the proton (also approximately 1.6×10−19C).
Step 2: Calculate the Acceleration of the Electron and Proton
- The acceleration of the electron (ae) can be calculated using Newton's second law:
ae=Feme=−eEme
where me is the mass of the electron (approximately 9.1×10−31kg).
- The acceleration of the proton (ap) is:
ap=Fpmp=eEmp
where mp is the mass of the proton (approximately 1.67×10−27kg).
Step 3: Use the Equation of Motion
- The distance fallen by both the electron and proton is h. Using the equation of motion s=ut+12at2 and noting that the initial velocity u=0:
h=12aet2e(for the electron)
h=12apt2p(for the proton)
Step 4: Relate the Times of Fall
- From the equations above, we can express the time of fall for the electron and proton:
t2e=2haeandt2p=2hap
- Taking the ratio of the squares of the times:
t2et2p=apae
Step 5: Substitute the Accelerations
- Substitute the expressions for ae and ap:
t2et2p=eEmp−eEme=memp
- This implies:
tetp=√memp
Step 6: Determine the Relationship Between the Times
- Since me (mass of the electron) is much smaller than mp (mass of the proton):
tetp<1
- This means that the time of fall of the electron te is less than the time of fall of the proton tp.
Conclusion
Thus, the time of fall of the electron, in comparison to the time of fall of the proton, is shorter.
- The force acting on the electron (Fe) in the upward electric field is given by:
Fe=−eE
where e is the charge of the electron (approximately 1.6×10−19C).
- The force acting on the proton (Fp) when the electric field is reversed (downward) is:
Fp=eE
where e is the charge of the proton (also approximately 1.6×10−19C).
- The acceleration of the electron (ae) can be calculated using Newton's second law:
ae=Feme=−eEme
where me is the mass of the electron (approximately 9.1×10−31kg).
- The acceleration of the proton (ap) is:
ap=Fpmp=eEmp
where mp is the mass of the proton (approximately 1.67×10−27kg).
- The distance fallen by both the electron and proton is h. Using the equation of motion s=ut+12at2 and noting that the initial velocity u=0:
h=12aet2e(for the electron)
h=12apt2p(for the proton)
- From the equations above, we can express the time of fall for the electron and proton:
t2e=2haeandt2p=2hap
- Taking the ratio of the squares of the times:
t2et2p=apae
- Substitute the expressions for ae and ap:
t2et2p=eEmp−eEme=memp
- This implies:
tetp=√memp
- Since me (mass of the electron) is much smaller than mp (mass of the proton):
tetp<1
- This means that the time of fall of the electron te is less than the time of fall of the proton tp.
Thus, the time of fall of the electron, in comparison to the time of fall of the proton, is shorter.
Topper's Solved these Questions
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - AIIMS
22 Videos
- SOLVED PAPERS 2018BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPERS 2018EXERCISE - Assertion and Reasons
10 Videos
- SOLVED PAPER 2017BOOK - DC PANDEY ENGLISHCHAPTER - SOLVED PAPER 2017EXERCISE - Solved papers 2017(JIPMER)
32 Videos
- WAVE OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - WAVE OPTICSEXERCISE - For JEE Advanced E. Integer Type Questions
13 Videos
Similar Questions
An electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View SolutionAn electron falls through a small distance in a uniform electric field of magnitude 2×104NC−1. The direction of the field reversed keeping the magnitude unchanged and a proton falls through the same distance. The time of fall will be
View Solution
Knowledge Check
An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
A1.3×102sB2.1×10−12sC1.6×10−10sD2.9×10−9s
An electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
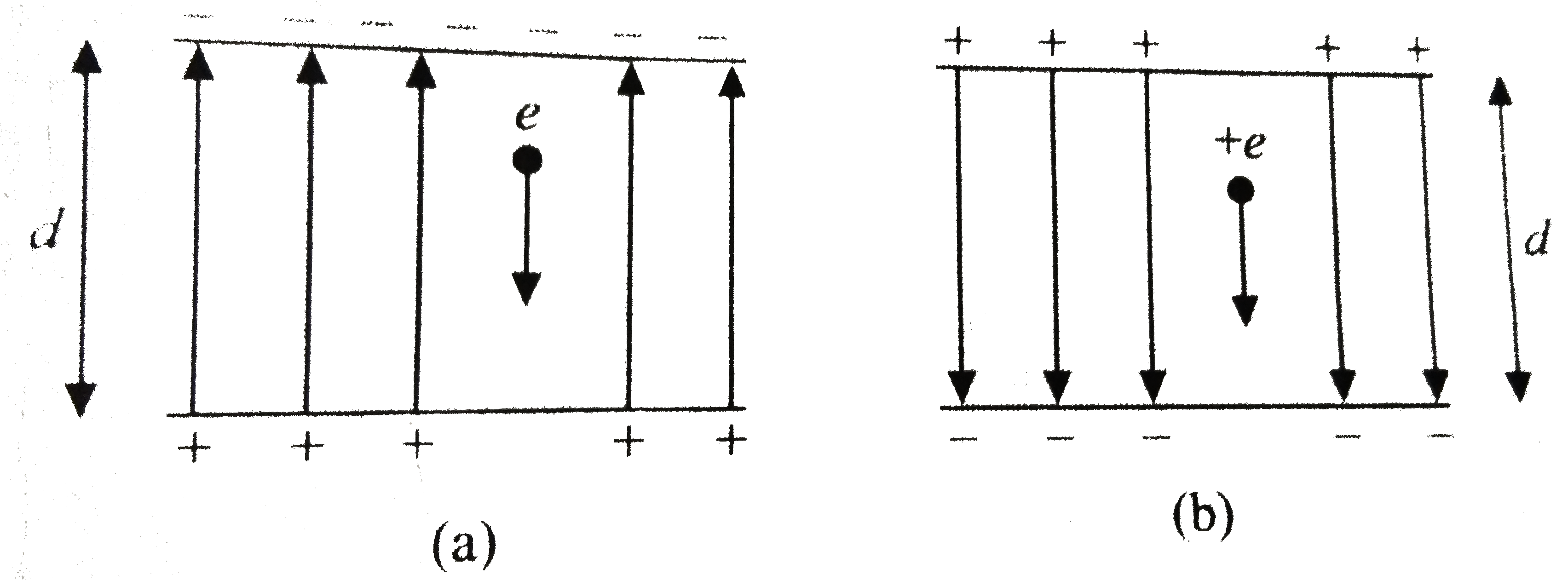 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.
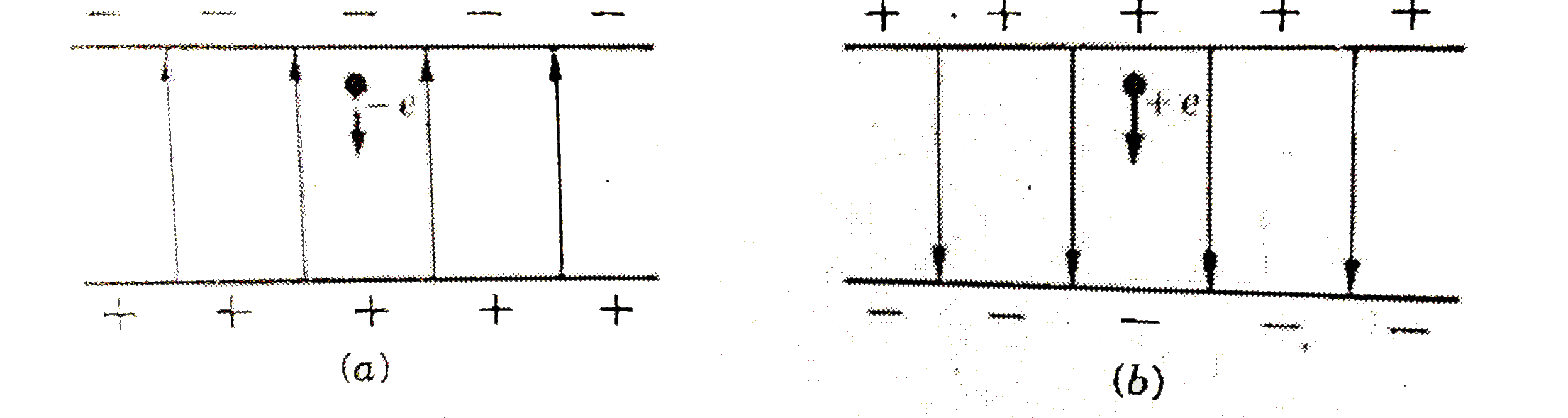
View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.4×104NC−1 [Fig.1.12 (a)]. The direction of the field is reversed keeping its magnitude unchagned and a proton falls through the same distance [Fig. 1.12 (b) ]. Complute the time of fall in each case. Contrast the situation (a) with that of free fall under gravity.
View SolutionA ball falls freely from rest. The ratio of the distance travelled in first, second, third and fourth second is
View SolutionAn object of mass 10 kg falls from rest through a vertical distance of 10 m and acquires a velocity of 10ms−1. The work done by the push of air on the object is (g=10ms−2)
View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0×104N/C(Fig.a)
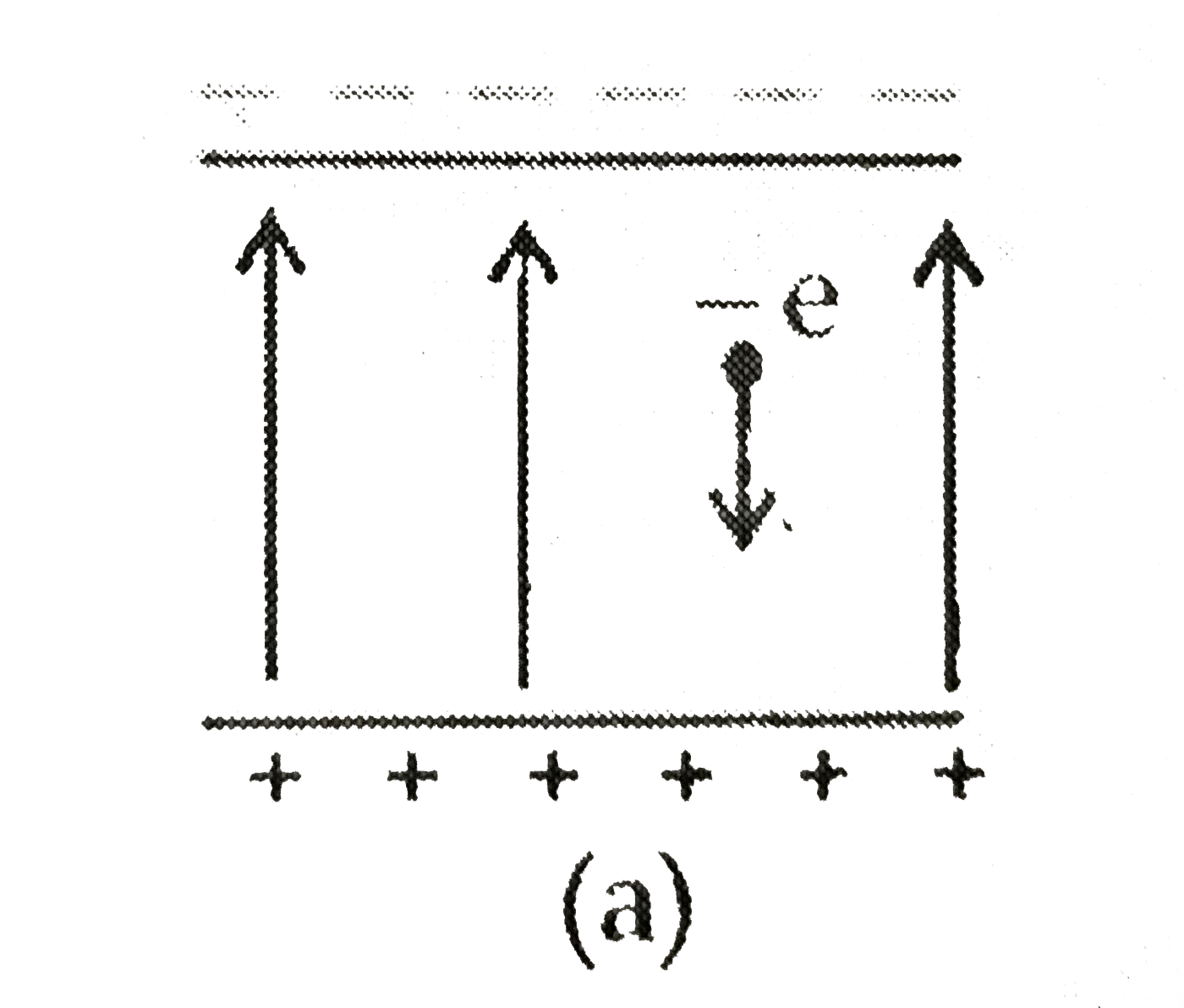
Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed (fig .b) keeping its magnitude unchanged , calculate the time taken by a proton to fall through this distance starting from rest.

View SolutionA proton and an α-particle start from rest in a uniform electric field, then the ratio of times of flight to travel same distance in the field is
View SolutionAn electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
View Solution
