Question

An electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius $R$.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
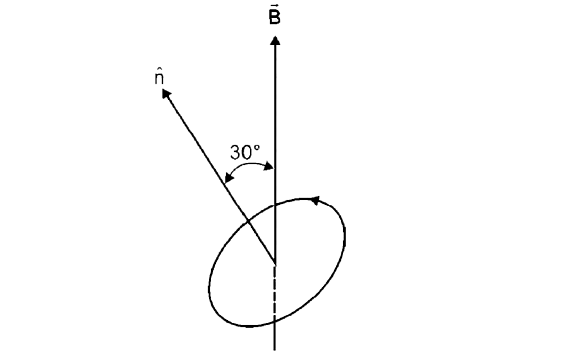
(ii) The atom is placed in a uniform magnetic induction $\overrightarrow{B}$ such that the plane - normal of the electron - orbit makes an angle of ${30}^{\circ }$ with the magnetic induction . Find the torque experienced by the orbiting electron.

Explanation

a. If `f` is the frequncy of orbital motion then the orbital magnetic dipole moment of circulating electron.
`M = I A = fe A`
According to Bohr's condition of stationary orbits
`m v R = n (h)/(2 pi)`
For ground state, `n = 1 and area A = pi R^(2)`
Also, `v = R omega = R 2 pif`
`:. m (R 2 pi f) R = 1 (h)/(2 pi)`
`:. f = (h)/(4 pi^(2) m R^(2))`
`:. From Eq (i), M = ((h)/(4 pi^(2) m R^(2))) e pi R^(2)`
`implies M = (eh)/(4 pi m) A - m^(2)`
b.The direction of magnetic moment is along normal to the plane of electron orbit , i.e., alone `hat n`
`tau = M B` sin theta `= ((eh)/(4 pi m))B sin 30^(@)`
i.e.`tau = (eh B)/(8 pi m)` newton xx meter