An electron is released from rest in a uniform electric field of magnitude 2.00×104N/C . (a) Calculate the acceleration of the electron. (Ignore gravitational) (b) How much time does the electron take to reach 1.00 % of the speed of light ?
Let's solve the problem step by step.
Given Data:
- Electric field (E) = 2.00×104N/C
- Charge of electron (q) = −1.6×10−19C (the negative sign indicates it's an electron)
- Mass of electron (m) = 9.1×10−31kg
- Speed of light (c) = 3.00×108m/s
Part (a): Calculate the acceleration of the electron.
1. Calculate the force on the electron using the formula:
F=q⋅E
Substituting the values:
F=(−1.6×10−19C)⋅(2.00×104N/C)=−3.2×10−15N
(The negative sign indicates the direction of the force is opposite to the electric field.)
2. Calculate the acceleration (a) using Newton's second law:
a=Fm
Substituting the values:
a=−3.2×10−15N9.1×10−31kg≈3.51×1015m/s2
Part (b): Calculate the time taken to reach 1% of the speed of light.
1. Calculate 1% of the speed of light:
v=0.01⋅c=0.01⋅(3.00×108m/s)=3.00×106m/s
2. Use the equation of motion v=u+at to find the time (t). Here, the initial velocity (u) is 0:
3.00×106m/s=0+(3.51×1015m/s2)⋅t
3. Rearranging the equation to solve for t:
t=3.00×106m/s3.51×1015m/s2≈8.55×10−10s
Summary of Results:
- (a) The acceleration of the electron is approximately 3.51×1015m/s2.
- (b) The time taken to reach 1% of the speed of light is approximately 8.55×10−10s or 0.855ns.
- Electric field (E) = 2.00×104N/C
- Charge of electron (q) = −1.6×10−19C (the negative sign indicates it's an electron)
- Mass of electron (m) = 9.1×10−31kg
- Speed of light (c) = 3.00×108m/s
F=q⋅E
Substituting the values:
F=(−1.6×10−19C)⋅(2.00×104N/C)=−3.2×10−15N
(The negative sign indicates the direction of the force is opposite to the electric field.)
a=Fm
Substituting the values:
a=−3.2×10−15N9.1×10−31kg≈3.51×1015m/s2
v=0.01⋅c=0.01⋅(3.00×108m/s)=3.00×106m/s
3.00×106m/s=0+(3.51×1015m/s2)⋅t
t=3.00×106m/s3.51×1015m/s2≈8.55×10−10s
- (a) The acceleration of the electron is approximately 3.51×1015m/s2.
- (b) The time taken to reach 1% of the speed of light is approximately 8.55×10−10s or 0.855ns.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Single Correct Choice Type)
45 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )
3 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
Knowledge Check
An electron initially at rest falls a distance of 1.5 cm in a uniform electric field of magnitude 2×104N/C. The time taken by the electron to fall this distance is
A1.3×102sB2.1×10−2sC1.6×10−10sD2.9×10−9sAn electron initially at rest falls a distance of 2 cm in a uniform electric field of magnitude 3×104NC−1. The time taken by the electron to fall to this distance is
A1.3×102sB2.1×10−12sC1.6×10−10sD2.75×10−9sAn electron is released from rest in a region of uniform electric and magnetic fields acting parallel to each other. The electron will
Amove in a straight line.Bmove in a circle.Cramain stationary.Dmove in a helical path.
A proton and an electron are placed in a uniform electric field. Which of the following is correct?
View SolutionAn electron falls through a distance of 1.5 cm in a uniform electric field of magnitude 2.0×104N/C(Fig.a)
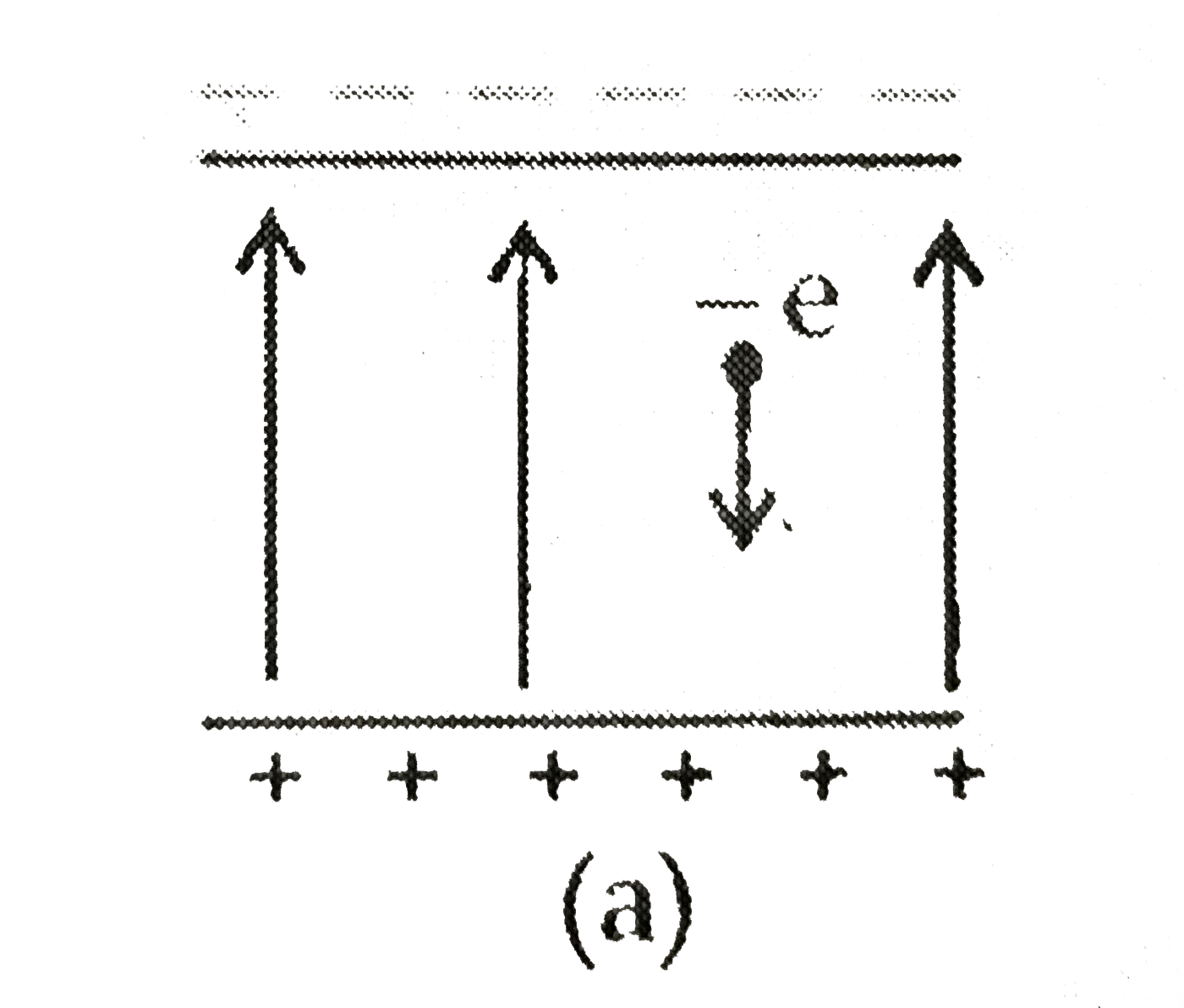
Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed (fig .b) keeping its magnitude unchanged, calculate the time taken by a proton to fall through this distance starting from rest.

View SolutionAn electron is released from rest at one point in uniform field and moves a distance of 10c cm in 10−7 s. What is the voltage between the points?
View SolutionAn electron is accelerated in an electric field of intensity E=3.0×106 N /C. Find the speed of the electron after 1.0 ns. What would be the speed of the electron, if 'its mass is independent of speed?
View SolutionAn electron falls through a distance 1.5 cm in a uniform electric field of magnitude 2.0×104NC−1 .Calculate the time it takes to fall through this distance starting from rest. If the direction of the field is reversed keeping its magnitude uncharged , calculate the time taken by a proton to fall through this distance starting from rest.
View Solution
