In the situation described in Problem 63, find the condition that a charge kept on x = 2m may be in a stable equilibrium. If the charge is of magnitude 1μC and has a mass of 3 g, find the time period of small oscillations of the body from its equilibrium position.
4π3s
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Single Correct Choice Type)
45 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (More than one correct Type )
3 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Check points
9 Videos
- ELASTICITYBOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- ELECTRIC POTENTIALBOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC POTENTIALEXERCISE - (PRACTICE QUESTIONS) Integer Type
1 Videos
Similar Questions
A massless rod of length L has two equal charges (q) tied to its ends. The rod is free to rotate in horizontal plane about a vertical axis passing through a point at a distance L4 from one of its ends. A uniform horizontal electric field (E) exists in the region. (a) Draw diagrams showing the stable and unstable equilibrium positions of the rod in the field. (b) Calculate the change in electric potential energy of the rod when it is rotated by an angle Δθ from its stable equilibrium position. (c) Calculate the time period of small oscillations of the rod about its stable equilibrium position. Take the mass of each charge to be m.
View SolutionConsider the situation of the previous problum. (a) Find the tension in the string in equilibrium. (b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
View SolutionA body of mass m is situated in a potential field U(x) = V0(1−cosax) when U0 and α are constants. Find the time period of small oscillations.
View SolutionPotential energy (U) of a body of unit mass moving in a one-dimension conservative force fileld is given by, U = (x2 – 4x + 3). All units are in S.I. (i) Find the equilibrium position of the body. (ii) Show that oscillations of the body about this equilibrium position is simple harmonic motion & find its timeperiod. (iii) Find the amplitude of oscillations if speed of the body at equilibrium position is 2√6 m/s.
View SolutionA body of mass m is situated in potential field U(x)=Uo(1−cos∝x) where, Uo and ∝ are constants. Find the time period of small oscillations.
View Solution(a) Derive and expression for the electric field at any point on the equatorial line of an electric dipole.
(b) Two identical point charges, q each kept 2m apart in air. A third point charge Q of unknown magnitude and sign is placed on the line joining the charges such that the system remains in equilibrium. Find the position and nature of Q.
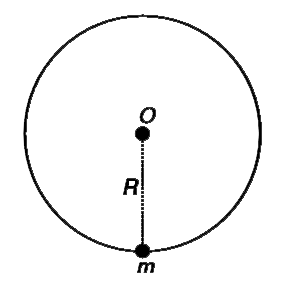
View SolutionA disc of mass M = 2m and radius R is pivoted at its centre. The disc is free to rotate in the vertical plane about its horizontal axis through its centre O. A particle of mass m is stuck on the periphery of the disc. Find the frequency of small oscillations of the system about its equilibrium position.
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
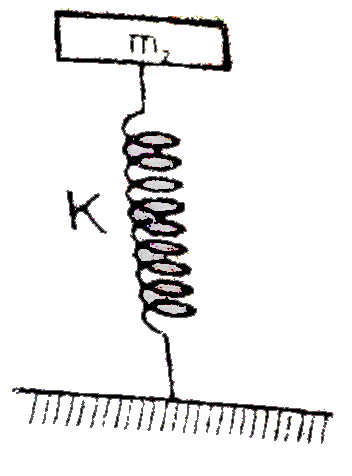
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
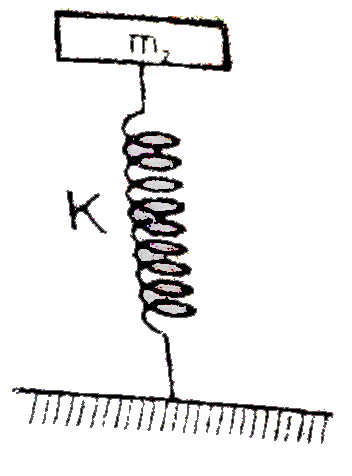
View SolutionBlock of mass m2 is in equilibrium as shown in figure. Anotherblock of mass m1 is kept gently on m2. Find the time period of oscillation and amplitude.
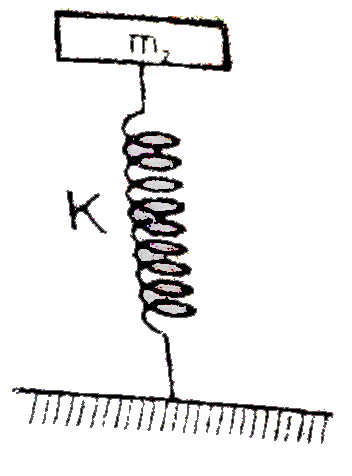
View Solution
