An electron moving in a circular orbit of radius r makes n rotations per second per second. The magnetic moment of the orbital electron is
zero
πr2ne
πr2n2e
r2ne2π
The correct Answer is:D
To find the magnetic moment of an electron moving in a circular orbit, we can follow these steps:
1. Understanding the Motion of the Electron:
An electron moving in a circular orbit can be considered as a current loop. The current (I) due to the electron's motion can be defined based on the number of rotations it makes per second.
2. Calculating the Current (I):
The current generated by the electron can be calculated using the formula:
I=eT
where e is the charge of the electron and T is the time period of one complete rotation. Since the electron makes n rotations per second, the time period T can be expressed as:
T=1n
Therefore, the current becomes:
I=e⋅n
3. Calculating the Area of the Circular Orbit:
The area A of the circular orbit can be calculated using the formula:
A=πr2
where r is the radius of the circular orbit.
4. Calculating the Magnetic Moment (μ):
The magnetic moment μ of a current loop is given by the formula:
μ=I⋅A
Substituting the expressions for I and A:
μ=(e⋅n)⋅(πr2)
Thus, the magnetic moment of the orbital electron is:
μ=e⋅n⋅πr2
Final Answer:
The magnetic moment of the orbital electron is:
μ=e⋅n⋅πr2
---
An electron moving in a circular orbit can be considered as a current loop. The current (I) due to the electron's motion can be defined based on the number of rotations it makes per second.
The current generated by the electron can be calculated using the formula:
I=eT
where e is the charge of the electron and T is the time period of one complete rotation. Since the electron makes n rotations per second, the time period T can be expressed as:
T=1n
Therefore, the current becomes:
I=e⋅n
The area A of the circular orbit can be calculated using the formula:
A=πr2
where r is the radius of the circular orbit.
The magnetic moment μ of a current loop is given by the formula:
μ=I⋅A
Substituting the expressions for I and A:
μ=(e⋅n)⋅(πr2)
Thus, the magnetic moment of the orbital electron is:
μ=e⋅n⋅πr2
The magnetic moment of the orbital electron is:
μ=e⋅n⋅πr2
Topper's Solved these Questions
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Papper 2
Explore 50 Videos
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Papper 3
Explore 50 Videos
- NUCLEIBook:NCERT FINGERTPS ENGLISHChapter:NUCLEIExercise:Assertion And Reason
Explore 15 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:NCERT Exemplar
Explore 11 Videos
Similar Questions
An electron moving in a circular orbit of radius r makes n rotation per second. The magnetic field produced at the centre has magnitude
View SolutionAn electron moving in a circular orbit of radius makes n rotations per second. The magnetic field produced at the centre has magnitude :
View SolutionAn electron revolving in an orbit of radius 0.5Å in a hydrogen atom executes per secon. The magnetic momentum of electron due to its orbital motion will be
View SolutionIn a hydrogen atom , the electron moves in an orbit of radius 0.5A making 10^( 16 ) revolutions per second . The magnetic moment associtated with the orbital motion of the electron is ……
View SolutionAn electron moving in a circular orbit of radius R with frequency f. The magnetic field at the centre of the orbit is
View SolutionAn electron of charge e is moving in a circular orbit of radius r around a nucleus, at a frequency v. The magnetic moment associated with the orbital motion of the electron is
View SolutionAn electron in a circular orbit of radius 0.05 mm performs 1016rev/s. the magnetic moment due to this rotation of electron is (∈A−m2).
View SolutionAn electron moves in circular orbit of radius r with constant speed v.The force acting in it is
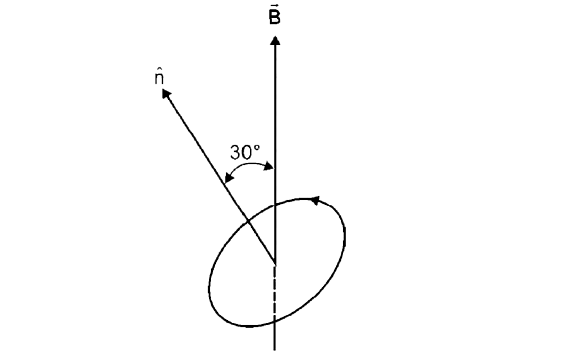
View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius R.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction →B such that the plane - normal of the electron - orbit makes an angle of 30∘ with the magnetic induction . Find the torque experienced by the orbiting electron.
View SolutionIn hydrogen atom , the electron moves in an orbit of radius 0.5 Å , making 1016 cps . Calculate magnetic moment associated with the orbital motion of electron ?
View Solution
