A voltmeter having a resistance of employed to measure the potential difference across a resistor which is connected to the terminals of a dc power supply having an emf of 50 V and an internal resistance of . What is the percentage decrease in the potential difference across the resistor as a result of connecting the voltmeter across it?
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Calculate the current flowing through the circuit without the voltmeter.
The total resistance in the circuit is the sum of the internal resistance of the power supply and the resistance of the resistor.
Given:
- EMF (E) = 50 V
- Internal resistance (r) = 20 Ω
- Resistor (R) = 200 Ω
Total resistance (R_total) = R + r = 200 Ω + 20 Ω = 220 Ω
Now, we can calculate the current (I) using Ohm's law:
I=ERtotal=50V220Ω=522A
Step 2: Calculate the potential difference across the 200 Ω resistor without the voltmeter.
The voltage across the 200 Ω resistor (V1) can be calculated using:
V1=E−I⋅r
Substituting the values:
V1=50V−(522A⋅20Ω)
Calculating the second term:
I⋅r=522⋅20=10022=5011V
Now substituting this back into the equation for V1:
V1=50−5011=55011−5011=50011V≈45.45V
Step 3: Calculate the equivalent resistance when the voltmeter is connected.
The voltmeter has a resistance of 1800 Ω, and it is connected in parallel with the 200 Ω resistor.
The equivalent resistance (R_eq) of two resistors in parallel is given by:
1Req=1R+1Rv
Where:
- R=200Ω
- Rv=1800Ω
Calculating R_eq:
1Req=1200+11800
Finding a common denominator:
1Req=91800+11800=101800=1180
Thus,
Req=180Ω
Step 4: Calculate the new total resistance with the voltmeter connected.
The new total resistance (R_total_new) is:
Rtotal_new=Req+r=180Ω+20Ω=200Ω
Step 5: Calculate the new current flowing through the circuit with the voltmeter connected.
Using Ohm's law again:
Inew=ERtotal_new=50V200Ω=14A
Step 6: Calculate the new potential difference across the 200 Ω resistor with the voltmeter connected.
The voltage across the 200 Ω resistor (V2) is given by:
V2=E−Inew⋅r
Calculating:
V2=50V−(14A⋅20Ω)
V2=50−5=45V
Step 7: Calculate the change in potential difference.
The change in voltage (ΔV) is:
ΔV=V1−V2=45.45V−45V=0.45V
Step 8: Calculate the percentage decrease in potential difference.
The percentage decrease is given by:
Percentage decrease=(ΔVV1)×100
Substituting the values:
Percentage decrease=(0.4545.45)×100≈0.99%
Final Answer:
The percentage decrease in the potential difference across the 200 Ω resistor as a result of connecting the voltmeter is approximately 1%.
---
The total resistance in the circuit is the sum of the internal resistance of the power supply and the resistance of the resistor.
- EMF (E) = 50 V
- Internal resistance (r) = 20 Ω
- Resistor (R) = 200 Ω
I=ERtotal=50V220Ω=522A
The voltage across the 200 Ω resistor (V1) can be calculated using:
V1=E−I⋅r
V1=50V−(522A⋅20Ω)
I⋅r=522⋅20=10022=5011V
V1=50−5011=55011−5011=50011V≈45.45V
The voltmeter has a resistance of 1800 Ω, and it is connected in parallel with the 200 Ω resistor.
1Req=1R+1Rv
Where:
- R=200Ω
- Rv=1800Ω
1Req=1200+11800
Finding a common denominator:
1Req=91800+11800=101800=1180
Req=180Ω
The new total resistance (R_total_new) is:
Rtotal_new=Req+r=180Ω+20Ω=200Ω
Using Ohm's law again:
Inew=ERtotal_new=50V200Ω=14A
The voltage across the 200 Ω resistor (V2) is given by:
V2=E−Inew⋅r
V2=50V−(14A⋅20Ω)
V2=50−5=45V
The change in voltage (ΔV) is:
ΔV=V1−V2=45.45V−45V=0.45V
The percentage decrease is given by:
Percentage decrease=(ΔVV1)×100
Percentage decrease=(0.4545.45)×100≈0.99%
The percentage decrease in the potential difference across the 200 Ω resistor as a result of connecting the voltmeter is approximately 1%.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 150videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 250videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Papper 250videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - NCERT Exemplar11videos
RAY OPTICS AND OPTICAL INSTRUMENTS
Similar Questions
If power dissipated in the 9Ω resistor in the resistor shown is 36W, the potential difference across the 2Ω resistor is
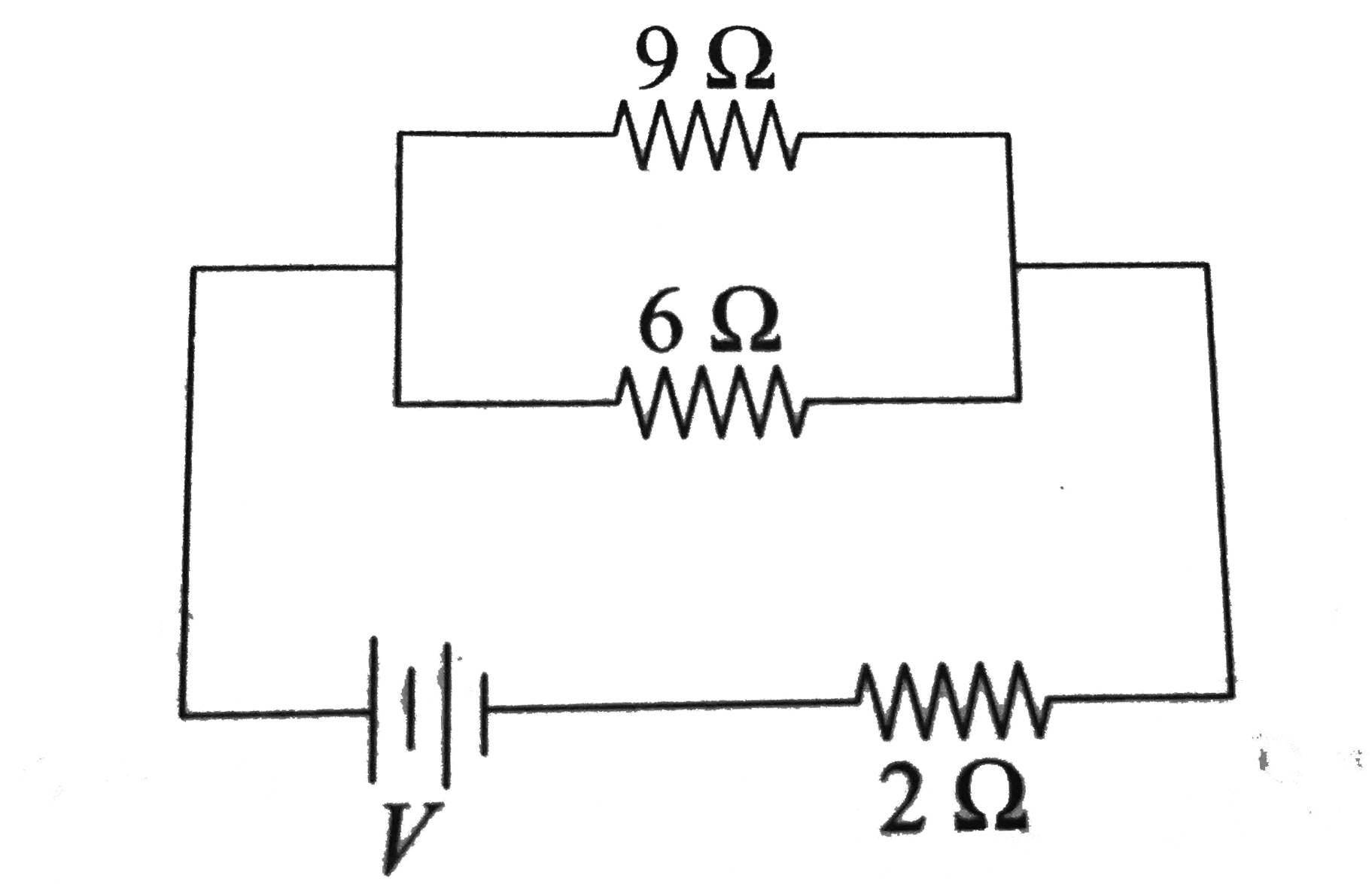 View Solution
View SolutionIf the power dissipated in the 27Ω resistor in the circuit shown is 108 watt, the potential difference across the 4Ω resistor is
View SolutionFind potential difference across the resistance 300Ω in A and B.
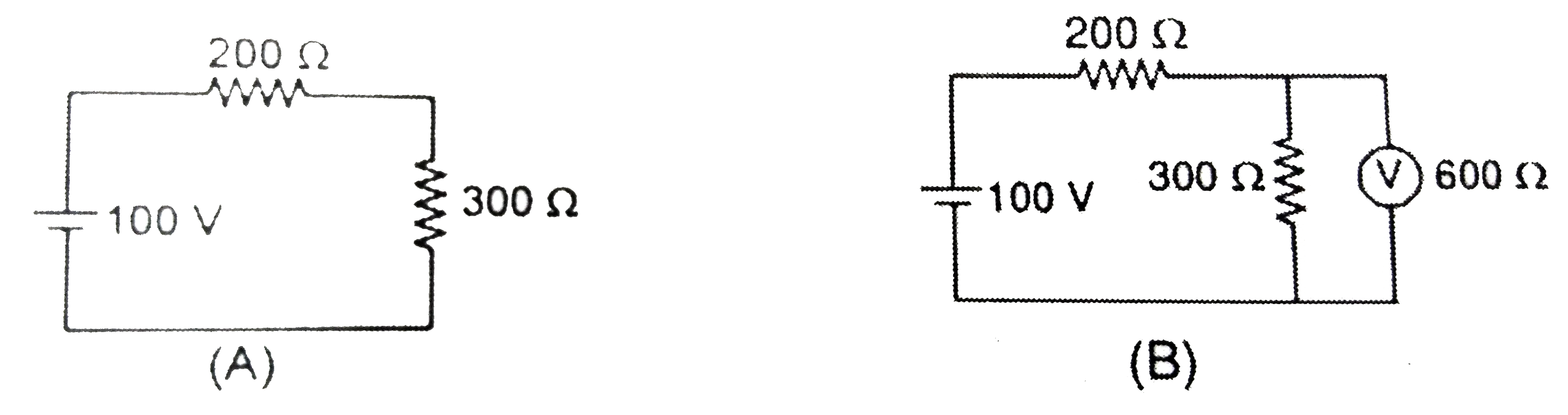 View Solution
View Solution100J of heat are produced each second in a 4Ω resistance. Find the potential difference across the resistor.
View SolutionA voltmeter of resistances 400(Ω)is used to measure the potential difference across the 100(Ω)resistor in the circuit shown in figure.(a) What will be the reading of the voltmeter ?(b) What was the potential difference across 100(Ω)before the voltmeter was connected ?
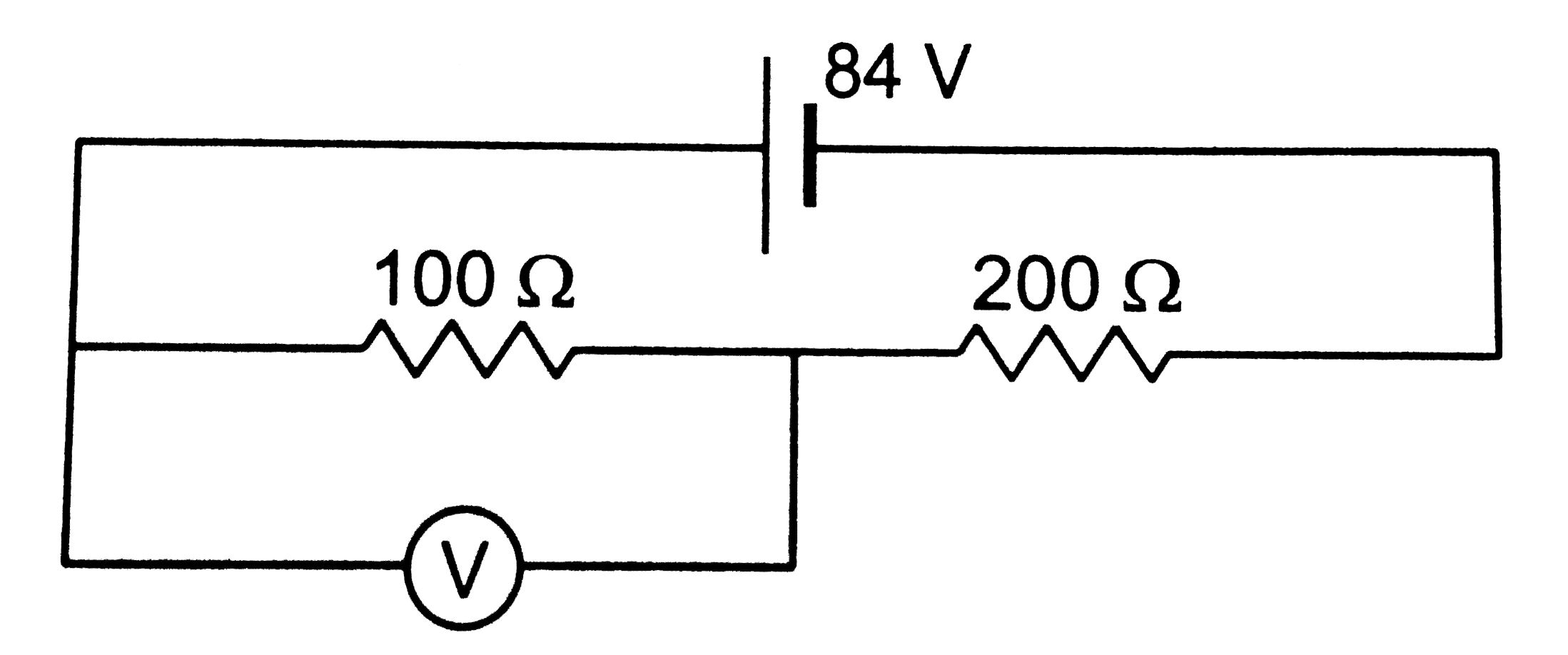 View Solution
View SolutionA high resistance voltmeter measures the potential difference across a battery to be 9-0 V. On connecting a 24 2 resistor across the terminals of the battery, the voltmeter reads 7.2 V. Calculate the internal resistance of the battery.
View SolutionThe cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View SolutionA cell has an emf 1.5V. When connected across an external resistance of 2Ω, the terminal potential difference falls to 1.0V. The internal resistance of the cell is:
View SolutionA resistor of 6 Ω is connected in series with another resistor of 4 Ω. A potential difference of 20 V is applied across the combination. Calculate :
the potential difference across the 6 Ω resistor.View SolutionFigure below shows two resistors R1andR2 connected to a battery having an emf of 40 V and negligible internal resistance. A voltmeter having a resistance of 300 Ω is used to measure potential difference across R1 Find the reading of the voltmeter.
 View Solution
View Solution


