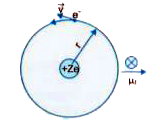
An electron of mass me, revolves around a nucleus of charge +Ze. Show that it behaves like a tiny magnetic dipole. Hence, prove that the magnetic moment associated with it is expressed as →μ=−e2me→L, where →L is the orbital angular momentum of the electron. Give the significance of negative sign.
We know that a revolving electron constitutes an electric current given by
I=eT=ev2πr
where T=2πrv = peroid of revolution of electron revolving in a circular orbit of radius r with a speed v.
∴ Magnetic moment (μl) associated with this circulating current,
μl=I⋅A=ev2πr⋅πr2=evr2
As an electron revolving is an anticlockwise direction is equivalent to current in clockwise direction, hence in accordance with right hand rule the magnetic moment is in a direction perpendicular to plane of paper (or plane of orbit) directed inward.
The above relation may also bewritten as :
μl=evrm2m=e2m⋅l
and in vector notation, →μl=−e2m⋅→l, where l=mvr = orbital angular momentum of the electron around the nucleus . The -ve sign applied here indicates that the angular momentum of the electorn is opposite in direction to the magnetic moment.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - LONG ANSWER QUESTIONS-II
11 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SELF ASSESSMENT TEST (SECTION A) (MULTIPLE CHOICE QUESTIONS)
5 Videos
- MOVING CHARGES AND MAGNETISM BOOK - U-LIKE SERIESCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - SHORT ANSWER QUESTIONS
41 Videos
- MODEL TEST PAPER 3 (UNSOLVED)BOOK - U-LIKE SERIESCHAPTER - MODEL TEST PAPER 3 (UNSOLVED)EXERCISE - SECTION A
3 Videos
- NUCLEIBOOK - U-LIKE SERIESCHAPTER - NUCLEIEXERCISE - Self Assessment Test
10 Videos
Similar Questions
A electron of mass, me revolves around a nucleus of charge +Ze. Show that it behaves like a tiny magnetic dipole. Hence, prove that the magnetic moment associated with it is expressed as →μ=−e2me→L, where →L is the orbital angular momentum of the electron. Give the signification of negative sign.
View SolutionA electron of mass, me revolves around a nucleus of charge +Ze. Show that it behaves like a tiny magnetic dipole. Hence, prove that the magnetic moment associated with it is expressed as →μ=−e2me→L, where →L is the orbital angular momentum of the electron. Give the signification of negative sign.
View Solution
Knowledge Check
If an electron of charge (-e) and mass me revolves around the nucleus of an atom having magnetic moment Me, then angular momentum of electron is
AL0=M0e2meBL0=e2M0meCL0=2M0meeDL0=2eM0meAn electron of chargee, revolves round in an orbit of radius r with a uniform angular velocity ω. The magnetic dipole moment of the electron in the orbit is
Aeωr/2Beωr2/2Ceω2r/2Deω2r2/2The ratio of magnetic dipole moment of an electron of charge e and mass m in the Bohr orbit in hydrogen to the angular momentum of the electron in the orbit is:
Ae/mBe/2mCm/eD2m/e
The ratio of magnetic dipole moment of an electron of charge e and mass m in the Bohr orbit in hydrogen to the angular momentum of the electron in the orbit is:
View SolutionAn electron of charge e is moving in a circular orbit of radius r around a nucleus, at a frequency v. The magnetic moment associated with the orbital motion of the electron is
View SolutionAn electron of charge e is moving in a circular orbit of radius r around a nucleus, at a frequency v. The magnetic moment associated with the orbital motion of the electron is
View SolutionIn a hydrogen atom, an electron of mass m and charge e revolves in an orbit of radius r making n revolutions per second. If the mass of hydrogen nucleus is M, the magnetic moment associated with the orbital motion of electron is
View SolutionWhat is the magnetic moment associated with the orbital motion of the electron if an electron of charge e moves in a circular orbit of radius r around the nucleus at a frequency v?
View Solution
