An ideal gas has initial volume V and pressure p. In doubling its volume the minimum work done will be in the process (of the given processes)
(a) isobaric process
(b) isothermal process
(c) adiabatic process
(d) same in all given processes
The correct Answer is:C
To determine the process in which the minimum work is done when an ideal gas doubles its volume from an initial volume V and pressure P, we can analyze the work done in different thermodynamic processes: isobaric, isothermal, and adiabatic.
1. Understanding Work Done in Thermodynamic Processes:
The work done W by a gas during expansion or compression can be calculated as the area under the PV curve. The formula for work done in a process can vary depending on the type of process.
2. Isobaric Process:
- In an isobaric process, the pressure remains constant.
- The work done is given by:
W=PΔV=P(Vf−Vi)
- Here, Vf=2V (final volume) and Vi=V (initial volume), so:
W=P(2V−V)=PV
3. Isothermal Process:
- In an isothermal process, the temperature remains constant.
- The work done can be calculated using:
W=nRTln(VfVi)
- Assuming one mole of gas (n=1), and using the ideal gas law, we can express R and T in terms of P and V:
W=PVln(2)
- This work done is greater than that in the isobaric process since ln(2)>1.
4. Adiabatic Process:
- In an adiabatic process, there is no heat exchange with the surroundings.
- The work done can be derived from the first law of thermodynamics and is given by:
W=PiVi−PfVfγ−1
- For an ideal gas undergoing adiabatic expansion, the work done is less than that in both isobaric and isothermal processes.
5. Comparison of Work Done:
- From our calculations:
- Isobaric: W=PV
- Isothermal: W=PVln(2)
- Adiabatic: W<PV (exact value depends on specific heat ratio γ)
- The adiabatic process results in the least amount of work done when doubling the volume.
Conclusion:
The minimum work done in doubling the volume of an ideal gas occurs during the adiabatic process.
The work done W by a gas during expansion or compression can be calculated as the area under the PV curve. The formula for work done in a process can vary depending on the type of process.
- In an isobaric process, the pressure remains constant.
- The work done is given by:
W=PΔV=P(Vf−Vi)
- Here, Vf=2V (final volume) and Vi=V (initial volume), so:
W=P(2V−V)=PV
- In an isothermal process, the temperature remains constant.
- The work done can be calculated using:
W=nRTln(VfVi)
- Assuming one mole of gas (n=1), and using the ideal gas law, we can express R and T in terms of P and V:
W=PVln(2)
- This work done is greater than that in the isobaric process since ln(2)>1.
- In an adiabatic process, there is no heat exchange with the surroundings.
- The work done can be derived from the first law of thermodynamics and is given by:
W=PiVi−PfVfγ−1
- For an ideal gas undergoing adiabatic expansion, the work done is less than that in both isobaric and isothermal processes.
- From our calculations:
- Isobaric: W=PV
- Isothermal: W=PVln(2)
- Adiabatic: W<PV (exact value depends on specific heat ratio γ)
- The adiabatic process results in the least amount of work done when doubling the volume.
The minimum work done in doubling the volume of an ideal gas occurs during the adiabatic process.
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 1 Objective Questions
1 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 1 Subjective
24 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 1 Assertion And Reason
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions
10 Videos
Similar Questions
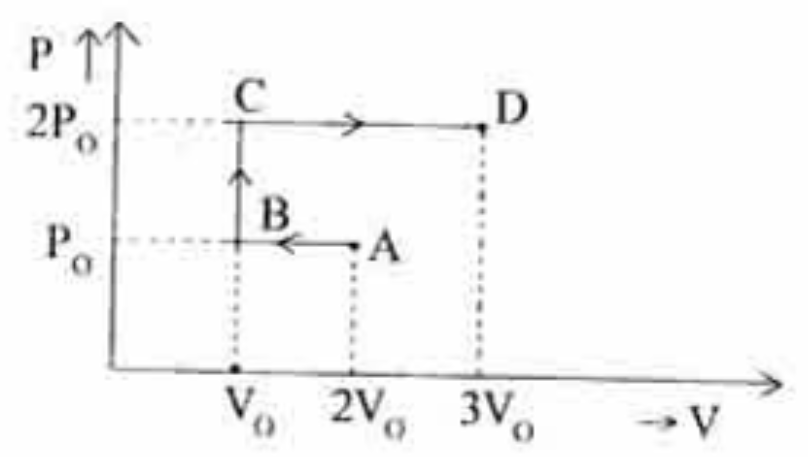
The work done by the gas in the process shown in given P-V diagram is
View SolutionAn ideal gas is initially at P1,V1 is expands to P2,V2 isothermally and then compressed adiabatically to the same volume V1 and pressure P3. If W is the net work done by the gas in complete process which of the following is true.
View SolutionAn ideal gas is initially at P1,V1 is expands isothermally to P2,V2 and then compressed adiabatically to the same volume V1 and pressure P3. If W is the net work done by the gas in complete process which of the following is true.
View SolutionAn ideal gas has an initial pressure of 3 pressure units and an initial volume of 4 volume units. The table gives the final pressure and volume of the gas (in those same units) in four processes. Whish process starts and ends on the same isotherm
View SolutionTemperature of two moles of an ideal gas is increased by 300K in a process V=aT, where a is positive constant. Find work done by the gas in the given process.
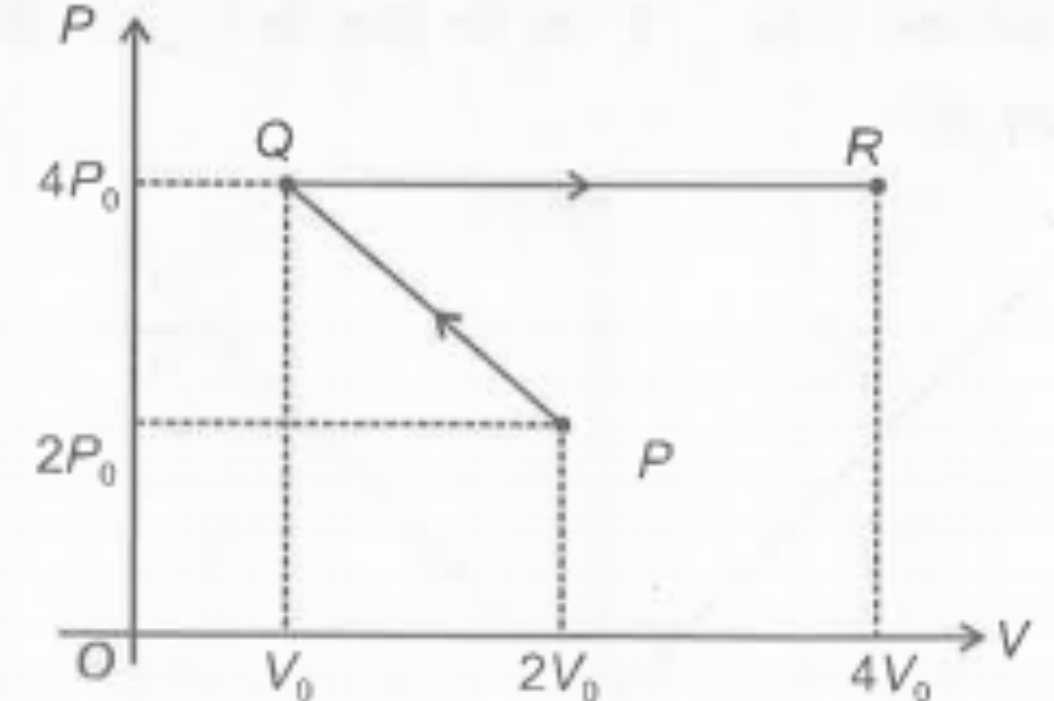
View SolutionAn ideal gas undergoes a process P→Q→R as shown in pressure (p) - volume (v) diagram.The work done by the gas is
View SolutionWork done by a sample of an ideal gas in a process A is double the work done in another process B. The temperature rises through the same amount in the two processes. If (C_A and C_B) be the molar heat capacities for the two processes,
View Solution16kg oxygen gas expands at STP to occupy double of its oxygen volume. The work done during the process is:
View SolutionAn ideal diatomic gas is expanded so that the amount of heat transferred to the gas is equal to the decrease in its internal energy. If in the process, the initial temperature of the gas be T0 and the final volume by 32 times the initial volume, the work done ( in Joules ) by the gas during the process will be
View Solution5 mole of an ideal gas of volume is expanded against vaccum to make its volume 2 times, then work done by the gas is:
View Solution
