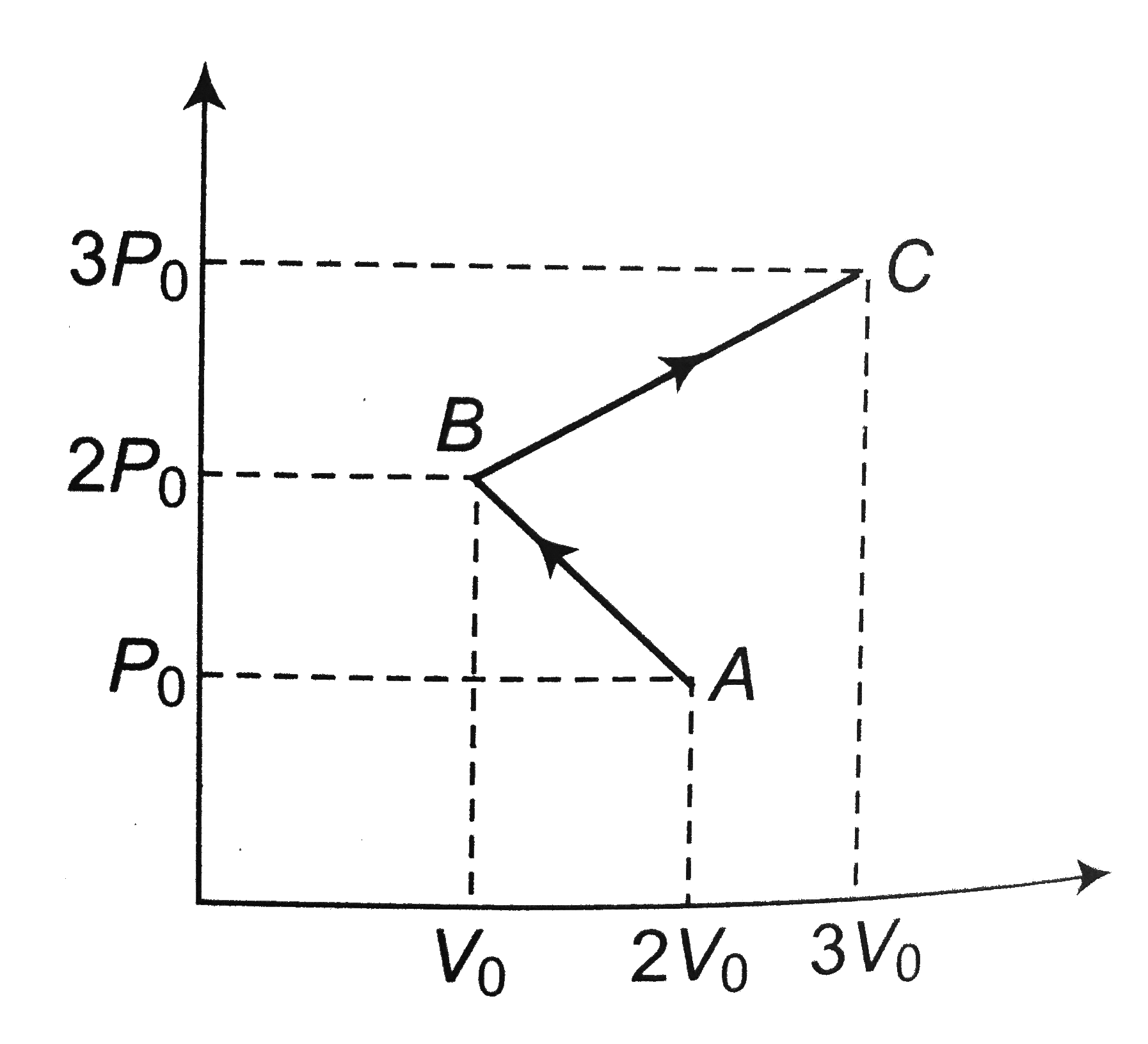
Work done by a sample of an ideal gas in a process A is double the work done in another process B. The temperature rises through the same amount in the two processes. If (C_A and C_B) be the molar heat capacities for the two processes,
CA=CB
CA<CB
CA>CB
CAandCB cannot be defined.
The correct Answer is:C
To solve the problem, we will analyze the relationship between the work done by an ideal gas in two different processes and the corresponding molar heat capacities. Here are the steps to arrive at the solution:
Step 1: Define the Work Done in Both Processes
Let the work done in process A be WA and in process B be WB. According to the problem, we have:
WA=2WB
Step 2: Relate the Change in Internal Energy
Since the temperature rises by the same amount in both processes, we can denote the change in temperature as ΔT. The change in internal energy ΔU for an ideal gas is given by:
ΔU=nCVΔT
where CV is the molar heat capacity at constant volume and n is the number of moles. Since the temperature change is the same in both processes, we have:
ΔUA=ΔUB
Step 3: Apply the First Law of Thermodynamics
According to the first law of thermodynamics:
Q=ΔU+W
For processes A and B, we can write:
QA=ΔUA+WA
QB=ΔUB+WB
Step 4: Express Heat Added in Terms of Heat Capacities
The heat added in each process can also be expressed in terms of the molar heat capacities:
QA=nCAΔT
QB=nCBΔT
Step 5: Substitute and Rearrange
Substituting the expressions for Q into the first law equations gives:
nCAΔT=nCVΔT+WA
nCBΔT=nCVΔT+WB
Step 6: Isolate Work Done
Rearranging these equations, we find:
WA=nCAΔT−nCVΔT
WB=nCBΔT−nCVΔT
Step 7: Substitute Work Done Relationship
Now, substituting WA=2WB into the first equation:
nCAΔT−nCVΔT=2(nCBΔT−nCVΔT)
Step 8: Simplify the Equation
This simplifies to:
nCAΔT−nCVΔT=2nCBΔT−2nCVΔT
nCAΔT+nCVΔT=2nCBΔT
Step 9: Factor Out Common Terms
Dividing through by nΔT (assuming n and ΔT are not zero):
CA+CV=2CB
Step 10: Rearranging for Comparison
Rearranging gives:
CA=2CB−CV
Conclusion
Since CV is always positive, we conclude that:
CA>CB
Thus, the molar heat capacity for process A is greater than that for process B.
Let the work done in process A be WA and in process B be WB. According to the problem, we have:
WA=2WB
Since the temperature rises by the same amount in both processes, we can denote the change in temperature as ΔT. The change in internal energy ΔU for an ideal gas is given by:
ΔU=nCVΔT
where CV is the molar heat capacity at constant volume and n is the number of moles. Since the temperature change is the same in both processes, we have:
ΔUA=ΔUB
According to the first law of thermodynamics:
Q=ΔU+W
For processes A and B, we can write:
QA=ΔUA+WA
QB=ΔUB+WB
The heat added in each process can also be expressed in terms of the molar heat capacities:
QA=nCAΔT
QB=nCBΔT
Substituting the expressions for Q into the first law equations gives:
nCAΔT=nCVΔT+WA
nCBΔT=nCVΔT+WB
Rearranging these equations, we find:
WA=nCAΔT−nCVΔT
WB=nCBΔT−nCVΔT
Now, substituting WA=2WB into the first equation:
nCAΔT−nCVΔT=2(nCBΔT−nCVΔT)
This simplifies to:
nCAΔT−nCVΔT=2nCBΔT−2nCVΔT
nCAΔT+nCVΔT=2nCBΔT
Dividing through by nΔT (assuming n and ΔT are not zero):
CA+CV=2CB
Rearranging gives:
CA=2CB−CV
Since CV is always positive, we conclude that:
CA>CB
Topper's Solved these Questions
Similar Questions
Knowledge Check
The work done in adiabatic process is given by
AnR(T1)−T2γBnR(T1)−T2γ−1C(nR(T1)−T2)RDγ(T1)−T2RnAn ideal gas system undergoes an isothermal process, then the work done during the process is
AnRTln(V2V1)BnRTln(V1V2)C2nRTln(V2V1)D2nRTln(V1V2)
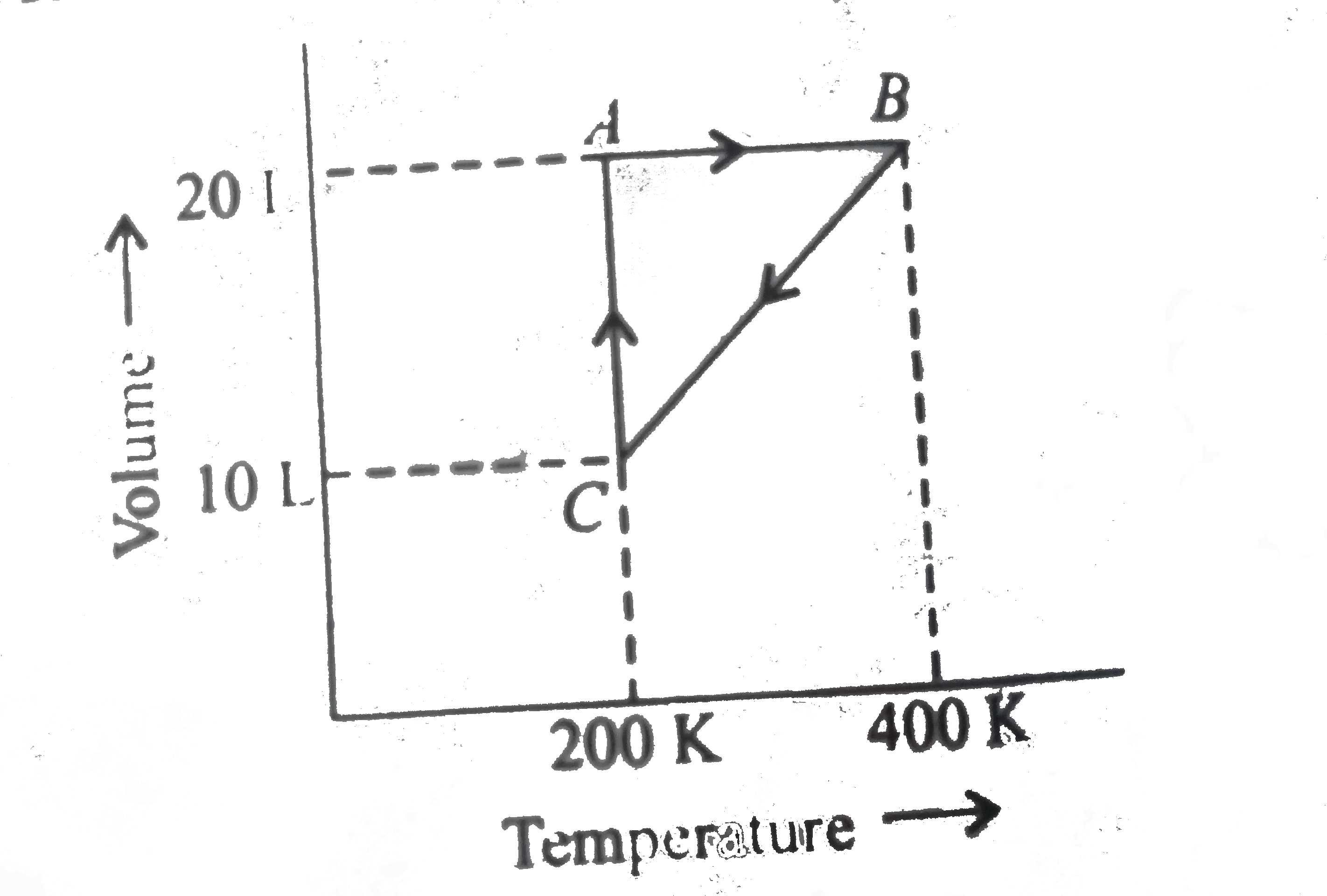
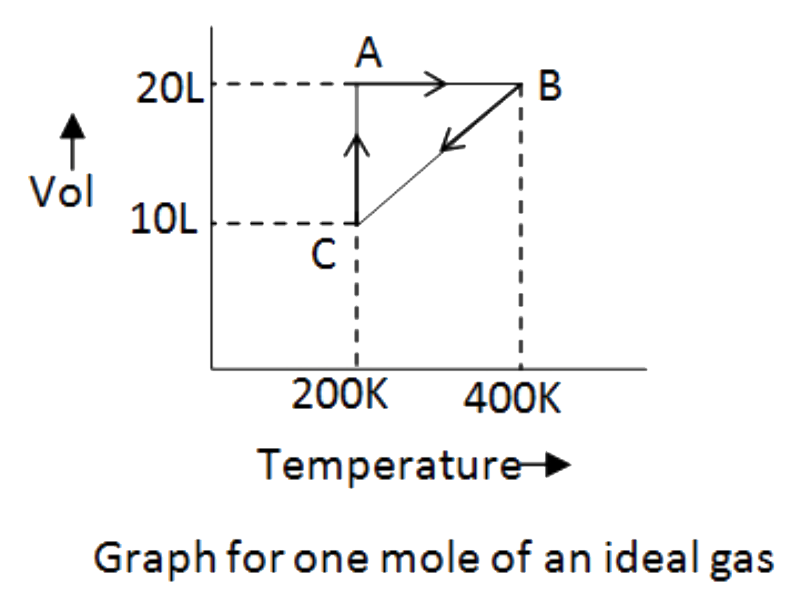
Work done in the process C→A is
View SolutionWork done for the process shownin the figure is

View SolutionThe work done by 1 mole of ideal gas during an adiabatic process is (are ) given by :
View SolutionFind work done in the irreversible process C→A.
View SolutionIdeal mono-atomic gas is taken through process such that dQ = 3dU. The molar heat capacity for process is:
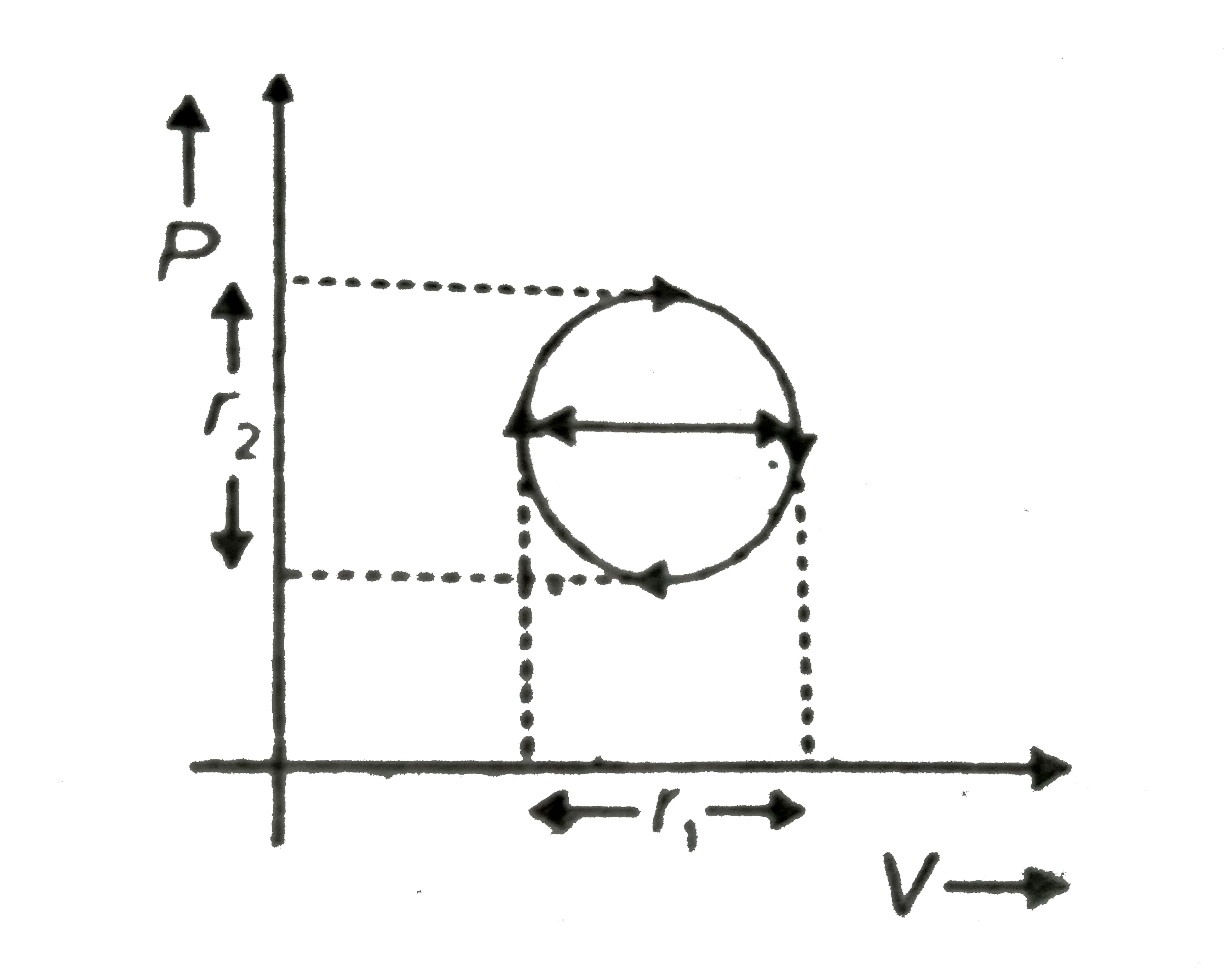
View SolutionA sample of gas is going through cyclic process, work done by gas is
View Solution