An inductor of 10mH is connected to a 18V battery through a resistor of 10k and a switch After a long time, when the maximum current is set up in the circuit, the current is switched off. Calculate the cur- rent in the circuit after 2 s.
To solve the problem step by step, we will follow the outlined procedure based on the information provided.
Step 1: Identify the given values
- Inductance (L) = 10 mH = 10×10−3 H
- Voltage (V) = 18 V
- Resistance (R) = 10 kΩ = 10×103 Ω
Step 2: Calculate the maximum current (I₀)
The maximum current in the circuit when the switch is closed can be calculated using Ohm's law:
I0=VR
Substituting the values:
I0=18V10×103Ω=1810000=1.8mA
Step 3: Calculate the time constant (τ)
The time constant (τ) for an RL circuit is given by:
τ=LR
Substituting the values:
τ=10×10−3H10×103Ω=10×10−310×103=10−6s=1μs
Step 4: Calculate the current after 2 microseconds (t = 2 µs)
The current in the inductor at any time t after the switch is opened can be calculated using the formula:
I(t)=I0(1−e−tτ)
Substituting t=2μs and τ=1μs:
I(2μs)=1.8×10−3(1−e−2×10−61×10−6)
This simplifies to:
I(2μs)=1.8×10−3(1−e−2)
Step 5: Calculate e−2
Using the approximate value:
e−2≈0.1353
So:
1−e−2≈1−0.1353=0.8647
Step 6: Final calculation of current
Now substituting back into the current equation:
I(2μs)=1.8×10−3×0.8647
Calculating this gives:
I(2μs)≈1.557mA
Final Answer
The current in the circuit after 2 microseconds is approximately 1.557 mA.
---
- Inductance (L) = 10 mH = 10×10−3 H
- Voltage (V) = 18 V
- Resistance (R) = 10 kΩ = 10×103 Ω
The maximum current in the circuit when the switch is closed can be calculated using Ohm's law:
I0=VR
Substituting the values:
I0=18V10×103Ω=1810000=1.8mA
The time constant (τ) for an RL circuit is given by:
τ=LR
Substituting the values:
τ=10×10−3H10×103Ω=10×10−310×103=10−6s=1μs
The current in the inductor at any time t after the switch is opened can be calculated using the formula:
I(t)=I0(1−e−tτ)
Substituting t=2μs and τ=1μs:
I(2μs)=1.8×10−3(1−e−2×10−61×10−6)
This simplifies to:
I(2μs)=1.8×10−3(1−e−2)
Using the approximate value:
e−2≈0.1353
So:
1−e−2≈1−0.1353=0.8647
Now substituting back into the current equation:
I(2μs)=1.8×10−3×0.8647
Calculating this gives:
I(2μs)≈1.557mA
The current in the circuit after 2 microseconds is approximately 1.557 mA.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IA58videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB18videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
Similar Questions
An inductor of 10mH is connected to a 18V battery through a resistor of 10kΩ and a switch. After a long time, when the maximum current is set up in the circuit, the battery is disconnected from the circuit. Calculate the current in the circuit after 15μs
View SolutionAn inductor of 3H is connected to a battery of emf 6V through a resistance of 100 Ω. Calculate the time constant. What will be the maximum value of current in the circuit ?
View SolutionAn idal coil of 10 is connected in series with a resitance of 5Ω and a battery of 5V. After 2s, after the connection is made, the current flowing ( in ampere) in the circuit is
View SolutionA coil of inductance L=50μH and resistance = 0.5Ω is connected to a battery of emf = 5V.
A resistance of 10Ω is connected parallel to the coil. Now, at the same instant the connection of the battery is switched off. Then, the amount of heat generated in the coil after switching off the battery isView SolutionAn inductor (L=20mH), a resistor (R=100Ω) and a battery (ε=10V) are connected in series. After along time the circuit is short- circuited and then the battery is disconnected. Find the current in the circuit 1ms after short- circuiting.
View SolutionAn L-R circuit has a cell of e.m.f. E , which is switched on at time t = 0. The current in the circuit after a long time will be
View SolutionTwo resistors, with resistance 10Ω and 15Ω, are to be connected to a battery of e.m.f. 12 V so as to obtain :
(i) minimum current (ii) maximum current
(a) Describe the mode of connecting the resistances in each case.
(b) Calculate the strength of the total current in the circuit in each case.View SolutionAn inductor (L = 100 mH), a resistor (R=100Ω) and a battery (E = 100 V) are initially connected in series as shown in the figure. After a long time the battery is disconnected after short circuiting the points A and B. The current in the circuit 1 ms after the short circuit is
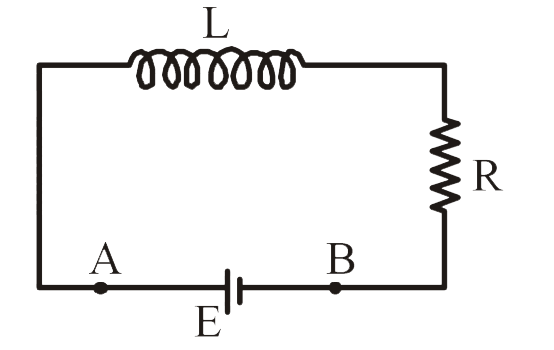 View Solution
View SolutionAn inductor L and a resistor R are connected in series to a battery, through a key/switch. Show graphically, how current decreases with time when the key/switch is opened.
View SolutionAn inductor of inductance 10 mH and a resistance of 5 is connected to a battery of 20 V at t = 0. Find the ratio of current in circuit at t = to current at t = 40 sec
View Solution

