A coil of inductance L=50μH and resistance = 0.5Ω is connected to a battery of emf = 5V.
A resistance of 10Ω is connected parallel to the coil. Now, at the same instant the connection of the battery is switched off. Then, the amount of heat generated in the coil after switching off the battery is
1.25 mJ
2.5 mJ
0.65 mJ
0.12 mJ
The correct Answer is:D
To solve the problem, we need to follow these steps:
Step 1: Calculate the current flowing through the inductor when the battery is connected.
The current I through the inductor can be calculated using Ohm's law. The total resistance in the circuit is the sum of the resistance of the coil R=0.5Ω and the parallel resistance Rp=10Ω.
The equivalent resistance Req of the parallel combination of Rp and R is given by:
1Req=1R+1Rp
Substituting the values:
1Req=10.5+110
Calculating this gives:
1Req=2+0.1=2.1⟹Req=12.1≈0.476Ω
Now, using Ohm's law, the current I can be calculated as:
I=EReq=5V0.476Ω≈10.51A
Step 2: Calculate the energy stored in the inductor.
The energy U stored in the inductor is given by the formula:
U=12LI2
Substituting the values:
U=12×50×10−6H×(10.51)2
Calculating this gives:
U≈12×50×10−6×110.53≈0.00276J=2.76mJ
Step 3: Determine the heat generated in the coil after switching off the battery.
When the battery is switched off, the energy stored in the inductor will be dissipated as heat in the resistances. The heat Q developed in the coil can be calculated using the formula:
Q=U⋅RR+Rp
Substituting the values:
Q=2.76mJ⋅0.50.5+10=2.76mJ⋅0.510.5
Calculating this gives:
Q≈2.76×0.510.5≈0.131mJ≈0.12mJ
Final Answer:
The amount of heat generated in the coil after switching off the battery is approximately 0.12 mJ.
---
The current I through the inductor can be calculated using Ohm's law. The total resistance in the circuit is the sum of the resistance of the coil R=0.5Ω and the parallel resistance Rp=10Ω.
The energy U stored in the inductor is given by the formula:
When the battery is switched off, the energy stored in the inductor will be dissipated as heat in the resistances. The heat Q developed in the coil can be calculated using the formula:
The amount of heat generated in the coil after switching off the battery is approximately 0.12 mJ.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns5videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point60videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A coil of inductance L=50μH and resistance =0.5Ω is connected to a battery of emf=5A. A resistance of 10Ω is connected parallel to the coil. Now at some instant the connection of the battery is switched off. Then the amount of heat generated in the coil after switching off the battery is (0.02)x in mJ. Find valuie of x.
View SolutionA coil of self inductance 2.5 H and resistance 20Ω is connected to a battery of emf 120 V having internal resistance of 5Ω. Find :
The time constant of the circuitView SolutionA coil of self inductance 2.5 H and resistance 20Ω is connected to a battery of emf 120 V having internal resistance of 5Ω. Find :
The current in the circuit in steady state.View SolutionA coil of inductance L=2.0μH and resitance R=1.0Ω is connected to a source of constant emfE=3.0V. A resistance Rs=2.0Ω is connected in parallel with the coil. Find the amount of heat generated in the coil after the swich Sw is disconnecied. The internal resistance of the source is negligible.
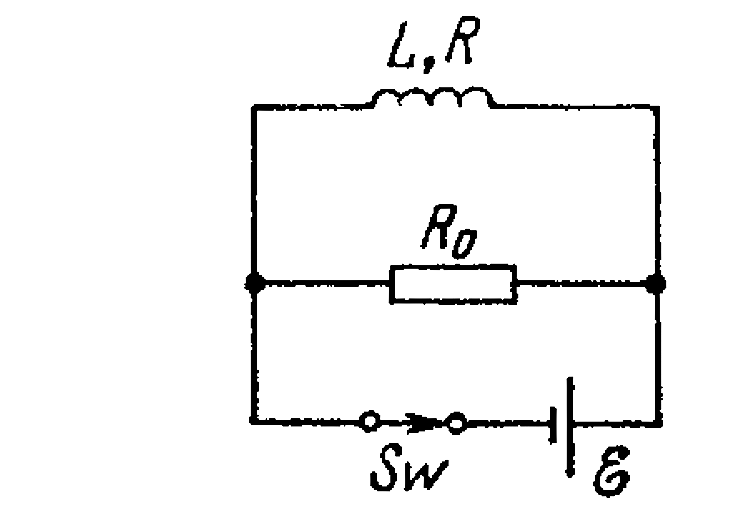 View Solution
View SolutionA coil of inductance 1.0 H and resistance 100 Omega is connected to a battery of emf 12 V. Find the energy stored in the magnetic field associated with the coil at an instant 10 ms after the circuit is switched on.
View SolutionA coil of inductance 8.4 mH and resistance 6(Ω) is connected to a 12 V battery. The current in the coil is 1.0 A at approximately the time
View SolutionA coil of inductance 8.4mH and resistance 6 Ω is connected to a 12V battery. The current in the coil is 1.0A at approximately the time.
View SolutionA coil of self inductance 10 mH and resistance 0.1 Ω is connected through a switch battery of internal resistance 0.9Ω after the switch is closed, the time taken for the current to attain 80% of the saturation value is [taken ln5=1.6]
View SolutionA coil having inductance 2.0 H and resistance 20Ω is connected to a battery of emf 4.0 V. Find (a) the current a the instant 0.20 s after the connection Is made and (b) the magnetic energy at this instant.
View SolutionA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
 . View Solution
. View Solution

