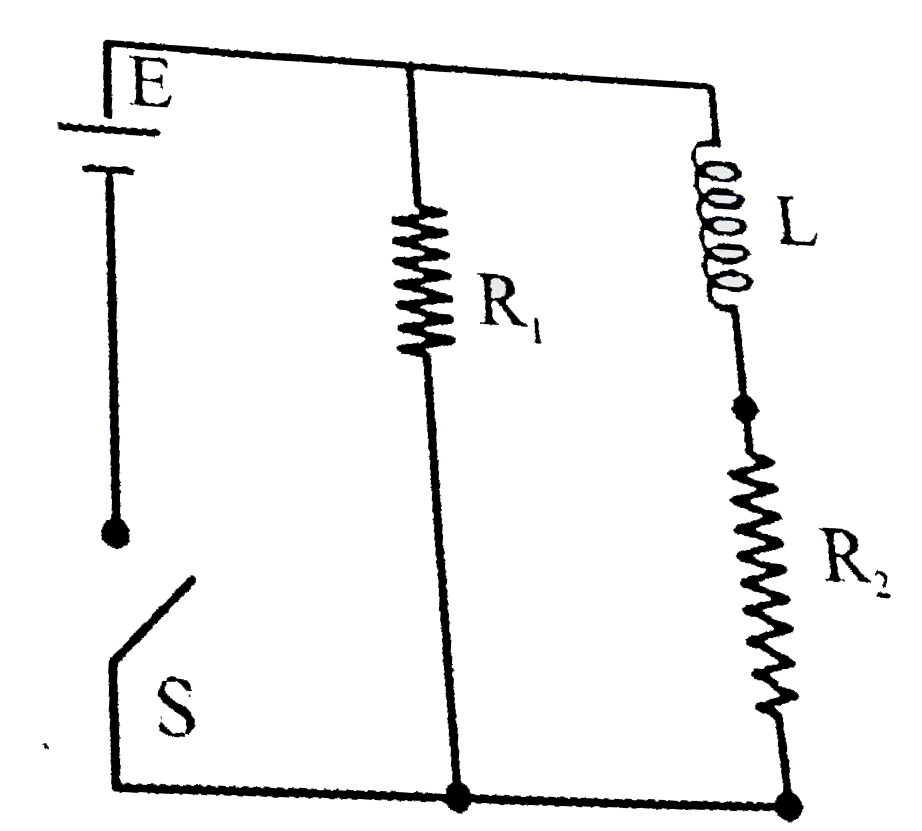
An inductor of inductance L = 400 mH and resistors of resistance R1=2Ω and R2=2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t=0. The potential drop across L as a function of time is
6e−5tV
12te−3tV
6(1−e−10.2)V
12e−5tV
The correct Answer is:D
E(across BC)=LdI2dt+R2I2 [using Kirchhoff's law]…(i)
I2=I0(I−e−t/t0)

At t = 0, I0=ER2=122=6A
τL=t0=LR=400×10−32Ω=0.2s
∴ I2=6(1−e−t/0.2) [using Eq. (i)]
Potential drop area L = E−R2I2
=12−2×6(1−e−t/0.2)=12e−t/0.2=12e−5tV
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Check point
60 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
An inductor of inductance L=400 mH and resistor of resistance R1=2(Ω)andR2=2(Ω) are connected to a battery of emf E = 12 Vas shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at time t =0. What is the potential drop across L as a function of time? After the steady state is reached, the switch is opened. What is the direction and the magnitude of current through R1 as a function of time?
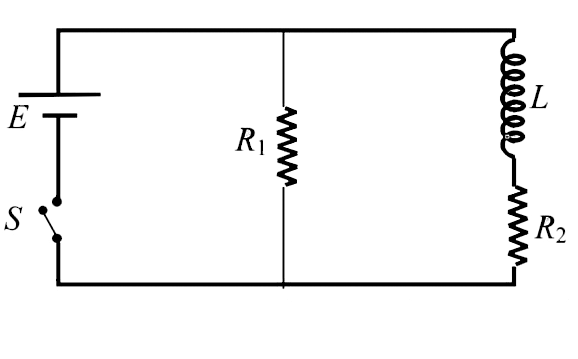
View SolutionAn inductor of inductance L=400mH and resistors of resistances R1=2Ω and R2=2Ω are connected to a battery of emf E=12V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at time t=0.

What is the potential dro across L s a function of time? After the steady state is reached, the switch is opened. What is the direction ad the magnitude of current throough R1 as a function of time?
View Solution
Knowledge Check
An inductor of inductance L = 400 mH and resistors of resistance R1=2Ω and R2=2Ω are connected to a battery of emf 12 V as shown in the figure. The internal resistance of the battery is negligible. The switch S is closed at t=0. The potential drop across L as a function of time is
 A12te−31VB6(1−e−t/0.2)VC12e−5tVD5e−5tV
A12te−31VB6(1−e−t/0.2)VC12e−5tVD5e−5tVA 4 m long wire of resistance 8Ω is connected in series with a battery of emf 2V and a resistor of 7Ω. The internal resistance of the battery is 1Ω. What is the potential gradient along the wire ?
A0.25Vm−1B0.50Vm−1C0.75Vm−1D1.00Vm−1A 4μF capacitor is connected to a battery of emf 24V. Through a resistance of 5MΩ and a switch which is kept open initially. Internal resistance of the battery is negligible. Switch is closed at t=0. Potential difference across capacitor and resistor at t=0 are respectively.
A12V, 12VB0V, 24VC24V, 0VD6V, 18V
An inductor of self-inductance L and resistor of resistance R are connected in series to a battery of emf E and negligible resistance.Calculate the maximum rate at which energy is stored in the inductor.
View SolutionA 5 V battery with internal resistance 2Ω and a 2V battery with internal resistance 1Ω are connected to a 10Ω as shown in the figure.
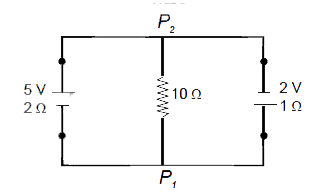
The current in the 10Ω resistance is
View SolutionAn inductor of inductance L and another resistor of resistance R are connected in series with a battery of emf E and a switch. Switch is closed at t = 0. How much charge will pass through the battery in one time constant? Internal resistance of the battery is negligible.
View SolutionShows a network of eight resistors battery of resistance R(=2Ω) connected in a 3V battery of negligible internal resistance. The current I in the circuit is
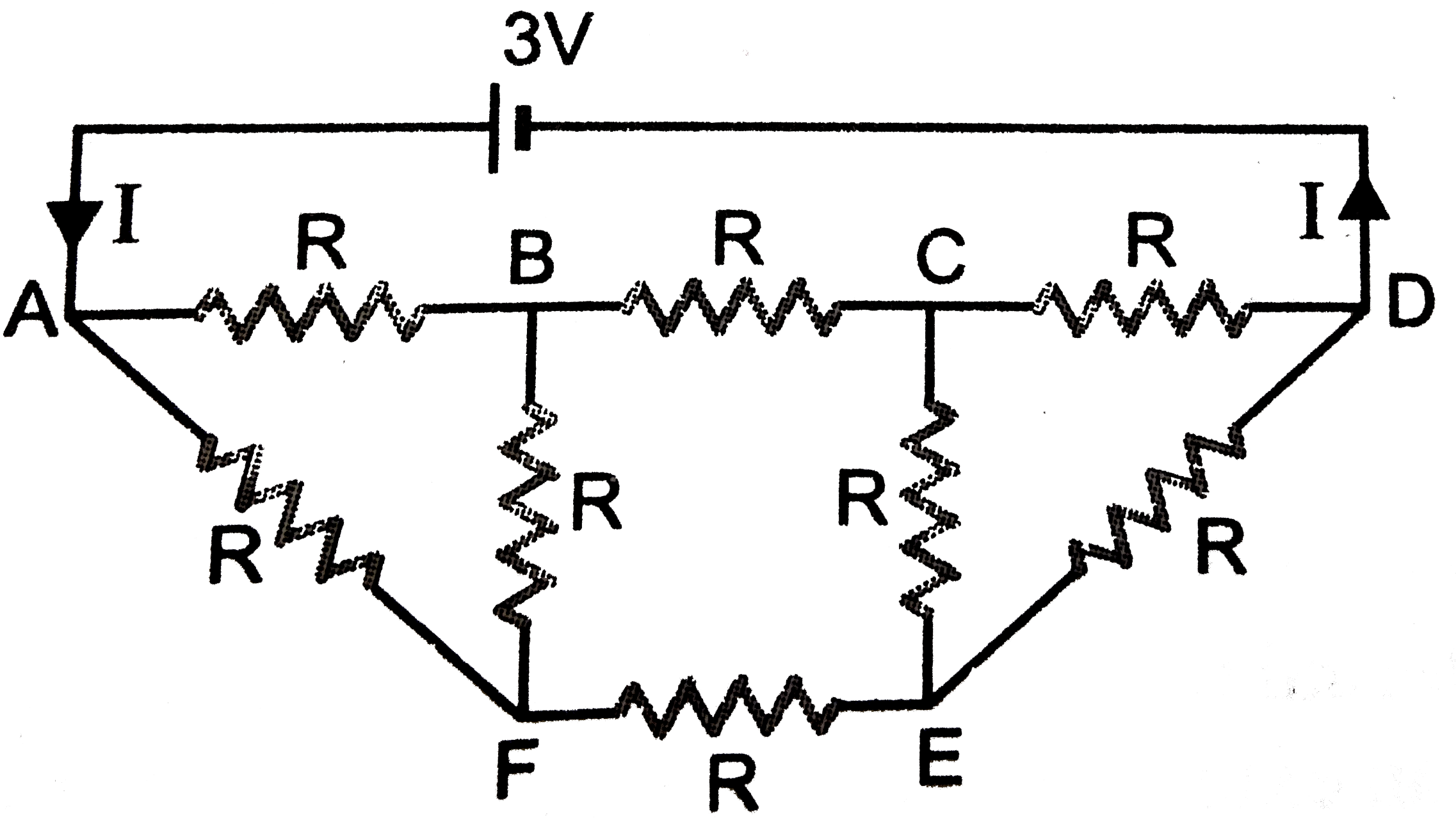
View SolutionTwo sources of emf 6V and internal resistance 3Ω and 2Ω are connected to anexternal resistance R as shown. If potential difference across battery A is zero, then the value of R ( in Ω) is
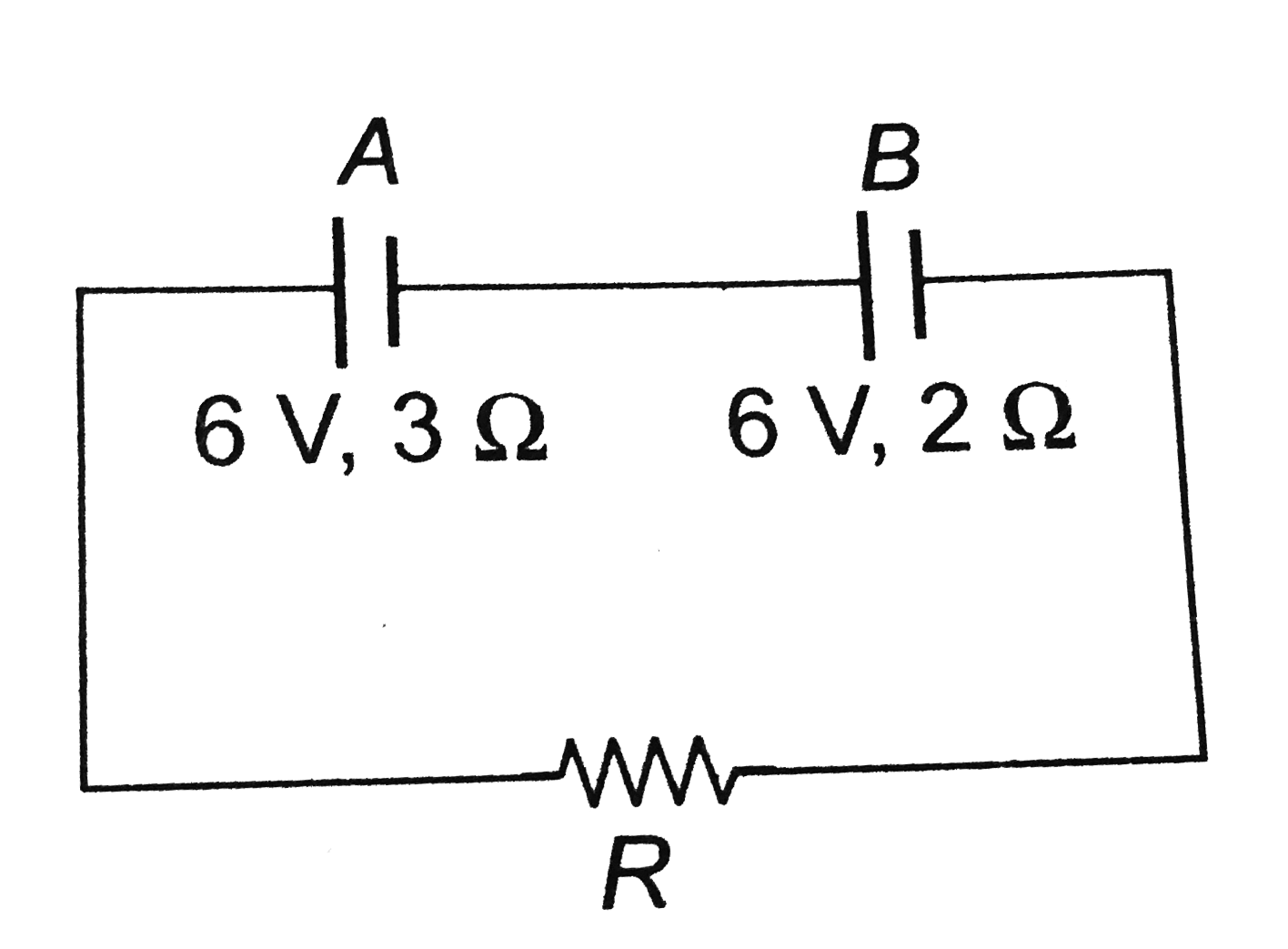
View Solution
