An inductor-resistance -battery circuit is switched on at t = 0. If the emf of the battery in one time constant tau.
To solve the problem of finding the charge that passes through the battery in one time constant τ in an LR circuit, we can follow these steps:
1. Understand the Circuit: We have an LR circuit consisting of an inductor (L), a resistor (R), and a battery with an emf (E). When the circuit is switched on at t=0, the current starts to increase.
2. Current Equation: The current I(t) in the circuit as a function of time is given by:
I(t)=I0(1−e−tτ)
where I0=ER is the maximum current and τ=LR is the time constant.
3. Charge Flow: The differential charge dq flowing through the battery in a small time dt is given by:
dq=I(t)dt
4. Integrate Charge Over One Time Constant: To find the total charge Q that passes through the battery in one time constant τ, we need to integrate dq from t=0 to t=τ:
Q=∫τ0I(t)dt=∫τ0I0(1−e−tτ)dt
5. Factor Out Constants: Since I0 is a constant, we can factor it out of the integral:
Q=I0∫τ0(1−e−tτ)dt
6. Evaluate the Integral: We can split the integral into two parts:
Q=I0(∫τ01dt−∫τ0e−tτdt)
The first integral evaluates to τ:
∫τ01dt=τ
The second integral can be evaluated using the substitution u=−tτ:
∫τ0e−tτdt=−τ(e−tτ)τ0=−τ(e−1−1)=τ(1−e−1)
7. Combine Results: Now substituting back into the equation for Q:
Q=I0(τ−τ(1−e−1))=I0τe−1
8. Final Expression: Thus, the total charge Q that passes through the battery in one time constant τ is:
Q=ER⋅τe−1
Simplifying gives:
Q=EτRe
Final Answer:
The charge that passes through the battery in one time constant τ is:
Q=EτRe
I(t)=I0(1−e−tτ)
where I0=ER is the maximum current and τ=LR is the time constant.
dq=I(t)dt
Q=∫τ0I(t)dt=∫τ0I0(1−e−tτ)dt
Q=I0∫τ0(1−e−tτ)dt
Q=I0(∫τ01dt−∫τ0e−tτdt)
The first integral evaluates to τ:
∫τ01dt=τ
The second integral can be evaluated using the substitution u=−tτ:
∫τ0e−tτdt=−τ(e−tτ)τ0=−τ(e−1−1)=τ(1−e−1)
Q=I0(τ−τ(1−e−1))=I0τe−1
Q=ER⋅τe−1
Simplifying gives:
Q=EτRe
The charge that passes through the battery in one time constant τ is:
Q=EτRe
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Short Answer13videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 112videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises9videos
ELECTROMAGNETIC WAVES
Similar Questions
Two inductors L1(inductors 1 mH, internal resistance 3 Ω) and L2 (inductance 2mH, internal resistance 4Ω),and a resistor R(resistance12ω) are all connected in parallelacross a 5 V battery. The circuit is switched on at time t=0. The ratio of the maximum to the minimum current (Imax/Imin) drawn from the battery is
View SolutionThe figure shows three circuit with identical batteries, inductors and resistance. Rank the circuit according to the currents through the battery just after the switch is closed greatest first :
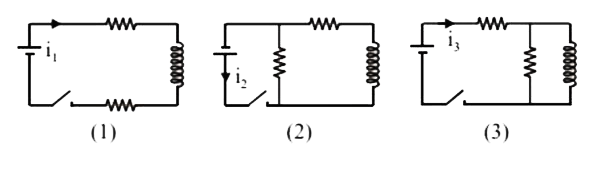 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A cricuite contains an inductance L, a resistance R and a battery of emf E. The circulit is switched on at t=0 . The change flows through the battery in one time constant (τ) is-
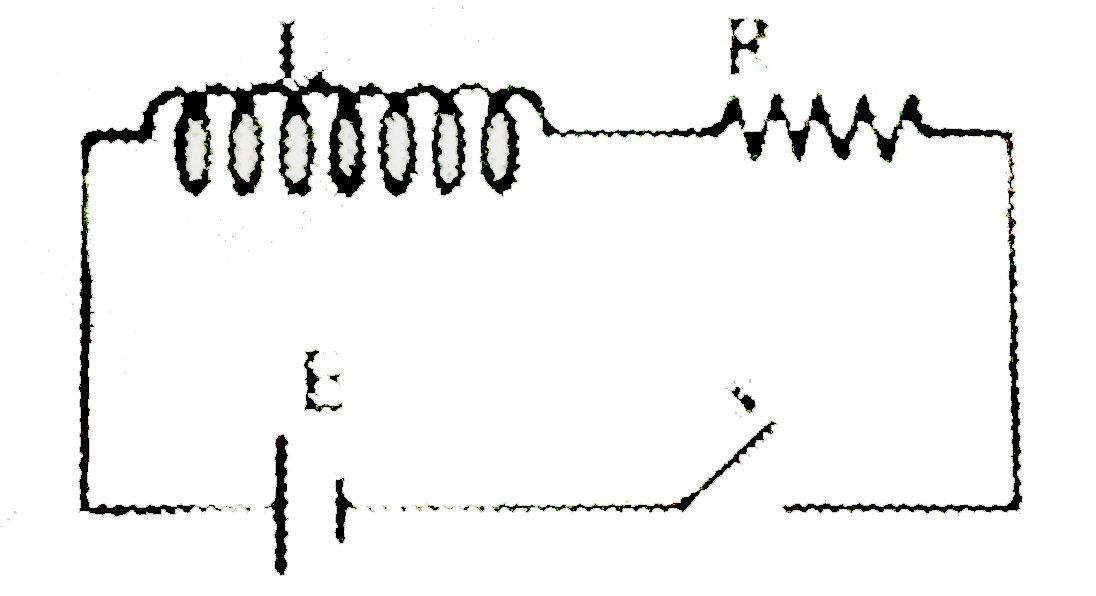 A2EτReBEτ2ReCEτReDzero
A2EτReBEτ2ReCEτReDzero - Question 2 - Select One
In the circuit shown in figure switch S is closed at time t=0. The charge which passes through the battery in one time constant is
 AeR2ELBE(LR)CELeR2DeLER
AeR2ELBE(LR)CELeR2DeLER - Question 3 - Select One
An inductance L and and a resistance R are connected in series to a battery of voltage V and negligible internal resistance through a switch. The switch is closed at t=0. The charge that passes through the battery in one time constant is [e is base of natural logarithms]
AeR2VLBVLRCVLeR2DeLVR
The figure below shows a battery of emf ε connected to an inductor L and resistance R in series. If the switch is closed at t=0, then the total charge that flows from the battery in time constant of the circuit is
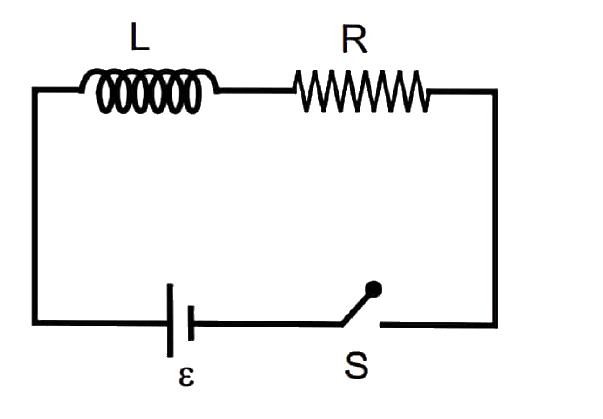 View Solution
View Solution5 A 50 mH inductor is in series with a 10 ohm resistor and a battery with an emf oj 25 V. At t = 0 the switch is closed. Find
Q(a) the time constant of the circuitView SolutionAn inductor of inductance L and another resistor of resistance R are connected in series with a battery of emf E and a switch. Switch is closed at t = 0. How much charge will pass through the battery in one time constant? Internal resistance of the battery is negligible.
View SolutionThe figure shows three circuits with identical batteries, inductors and resistance, Rank the circuits according to the currents through the battery just after the switch is closed, greatest first :
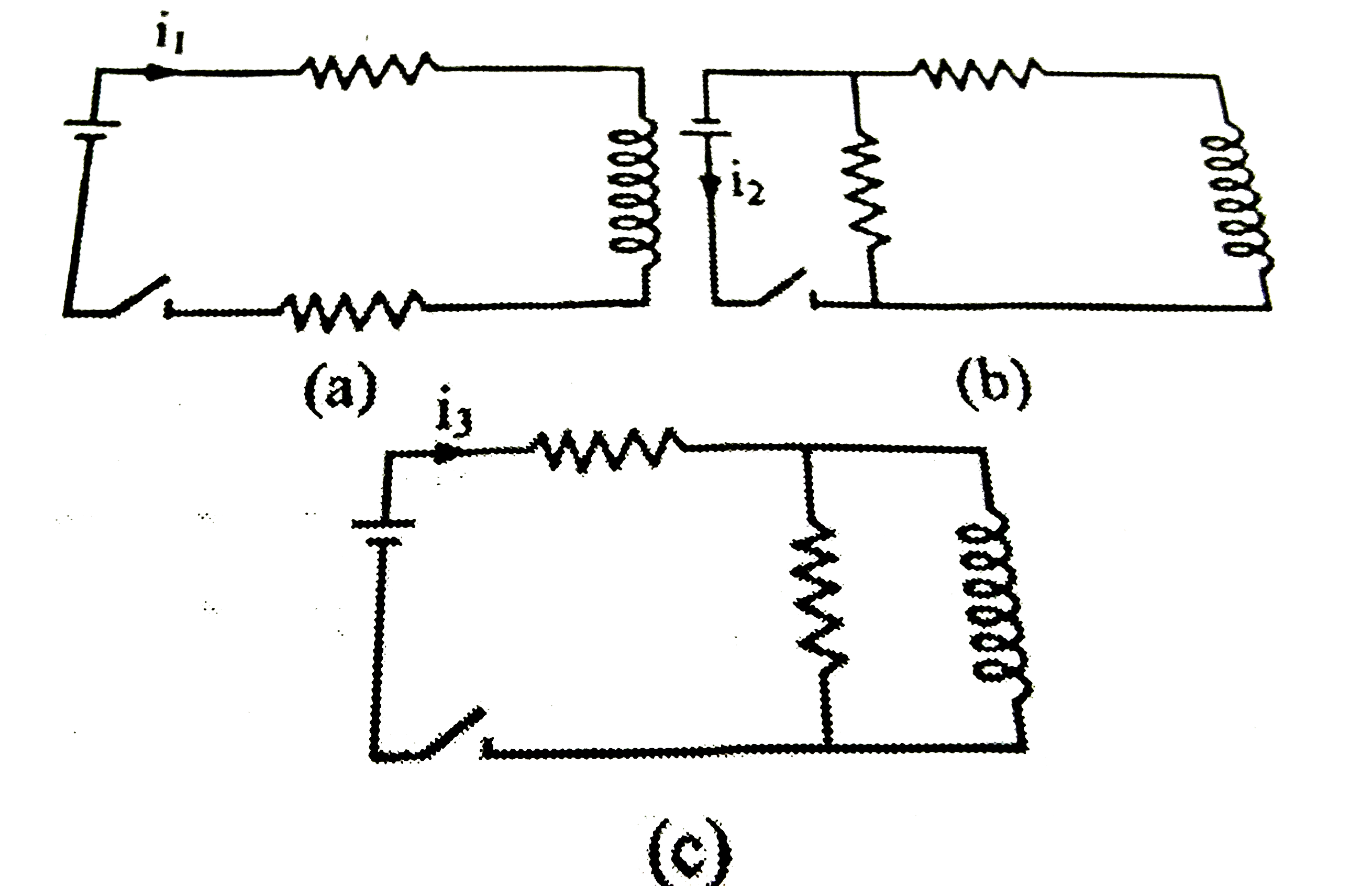 View Solution
View SolutionIn a circuit made up of inductor, resistance, ammeter, battery, and switch in series, at which of the following times after the switch is closed is the rate of increase of current greatest?
View Solution

