An infinite long straight wire with current I flowing along the positve z-axis is located at coordinates P(−12m,5m). Determine the unit vector showing the direction of magnetic field at the origin.
113(12ˆi+5ˆj)
113(5ˆi+12ˆj)
113(5ˆi−12ˆj)
113(−5ˆi+12ˆj)
The correct Answer is:B
Unit vector of ˆub
ˆub=ˆicos(90−θ)+ˆjcosθ=sinθˆi+cosθˆj
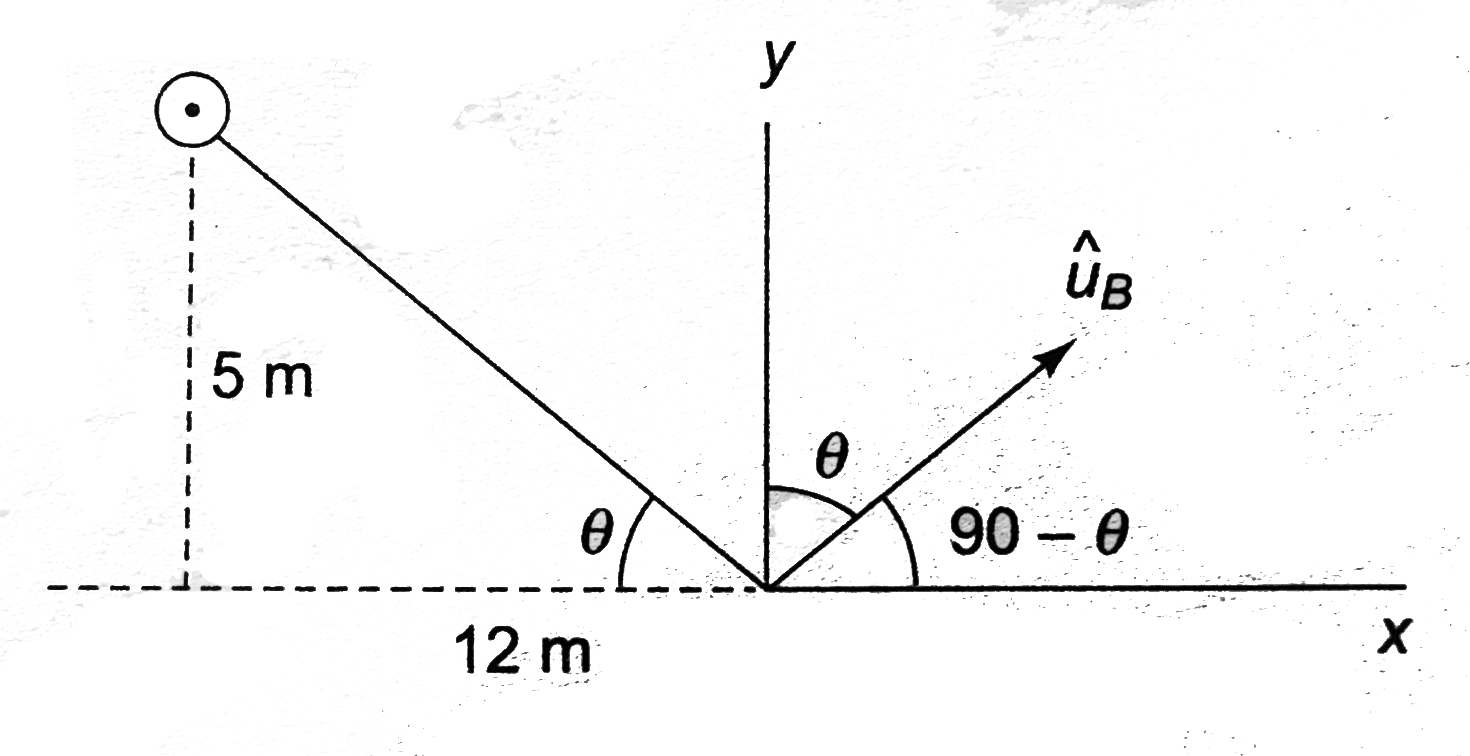
sinθ=5√52+122=513,cosθ=12√52+122=1213
ˆuB=513ˆi+1213ˆj=113(5ˆi+12ˆj)
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.2
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (subjective )
10 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Solved Example
20 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
Knowledge Check
An infinitely long wire carrying current I is along Y-axis such taht its one end is at point A(0,b) while the wire extends upto +∞. The magnitude of magnetic field strength at point (a,0) is
 Aμ0I4πa(1+b√a2+b2)Bμ0I4πa(1−b√a2+b2)Cμ0I4πa(b√a2+b2)Dnone of these
Aμ0I4πa(1+b√a2+b2)Bμ0I4πa(1−b√a2+b2)Cμ0I4πa(b√a2+b2)Dnone of theseThree infinitely long thin conductors are joined at the origin of coordinates and lie along the x-y- and z-axes. A current i flowing along the conductor lying along the x-axis divides equally into the othere two at the origin. The magnetic field at the point (0,-a,0) has magnitude
Aμ0i4πaB3μ0i4√2πaC√5μ0i8πaD√3μ0i2πaInfinite number of straight wires each carrying current I are equally placed as shown in the figure Adjacent wires have current in opposite direction Net magnetic field at point P is
 .Aμ0I4πIn2√3aˆkBμ0I4πIn4√3aˆkCμ0I4πIn4√3a(−ˆk)Dzero
.Aμ0I4πIn2√3aˆkBμ0I4πIn4√3aˆkCμ0I4πIn4√3a(−ˆk)Dzero
(a) Find the magnetic field at the point O if the wire carrying a current i has the shape shown. The radius of the current part of the wire is R, the linear parts of the wire are very long.
(i)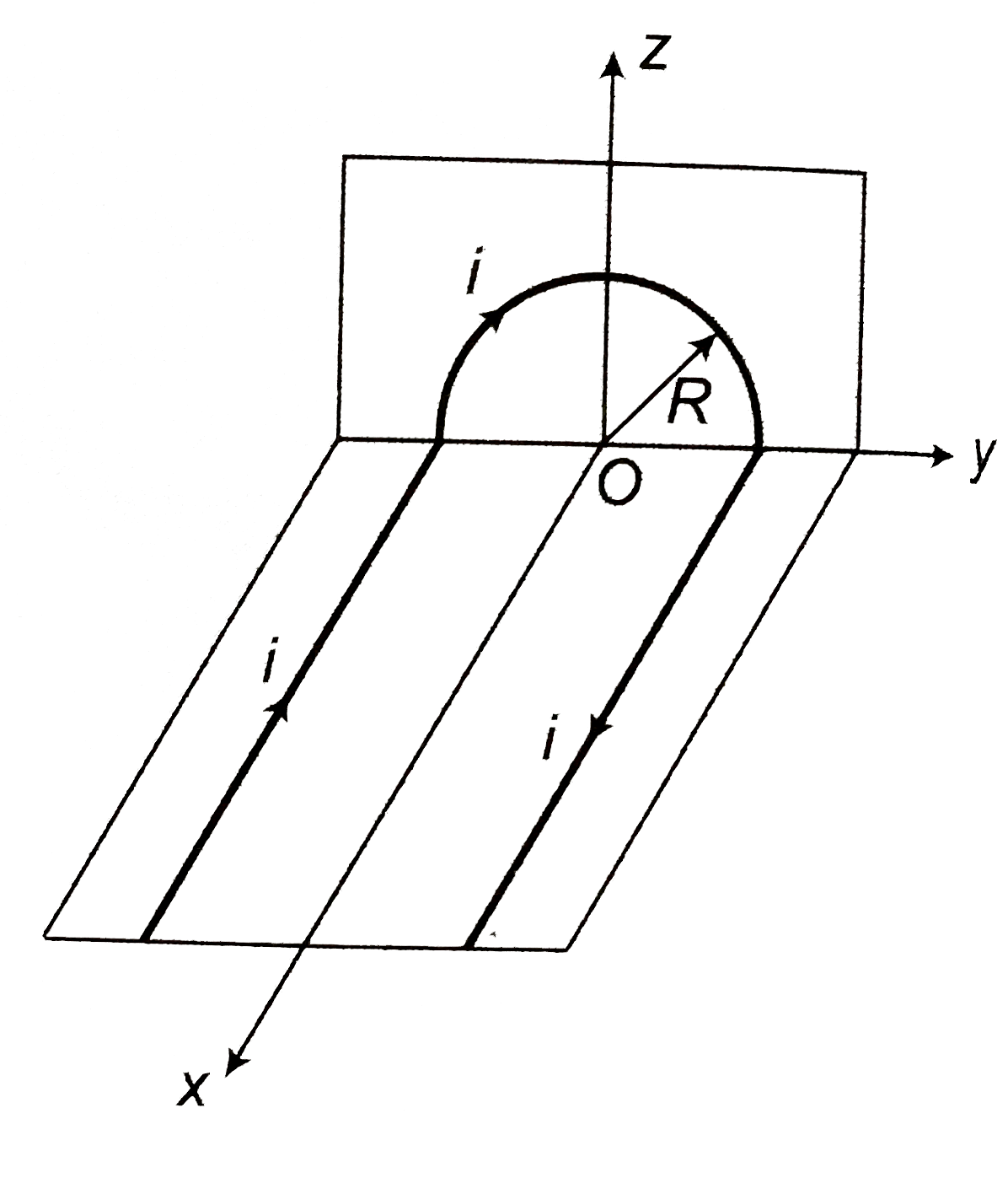
(ii)
(iii)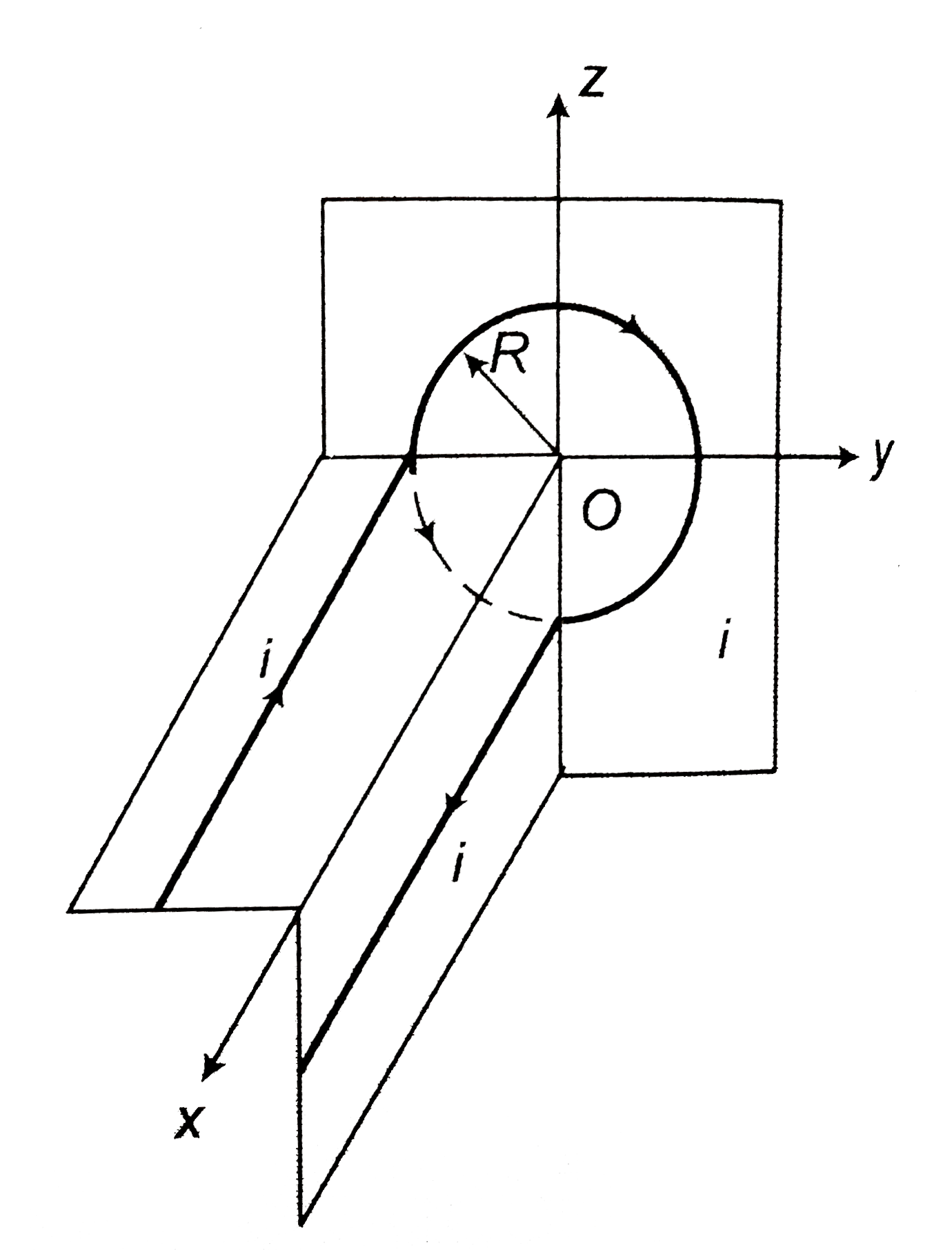
(b) A long straight wire along the z-axis carriers a current i in negative z-direction. Find magnetic field in vector from at a point having co-ordinates (x,y) on z=0 plane.
(c) A non-coplaner loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop of length 2a. find unit vector along magnetic field magnetic filed at the point P(a,0,a).
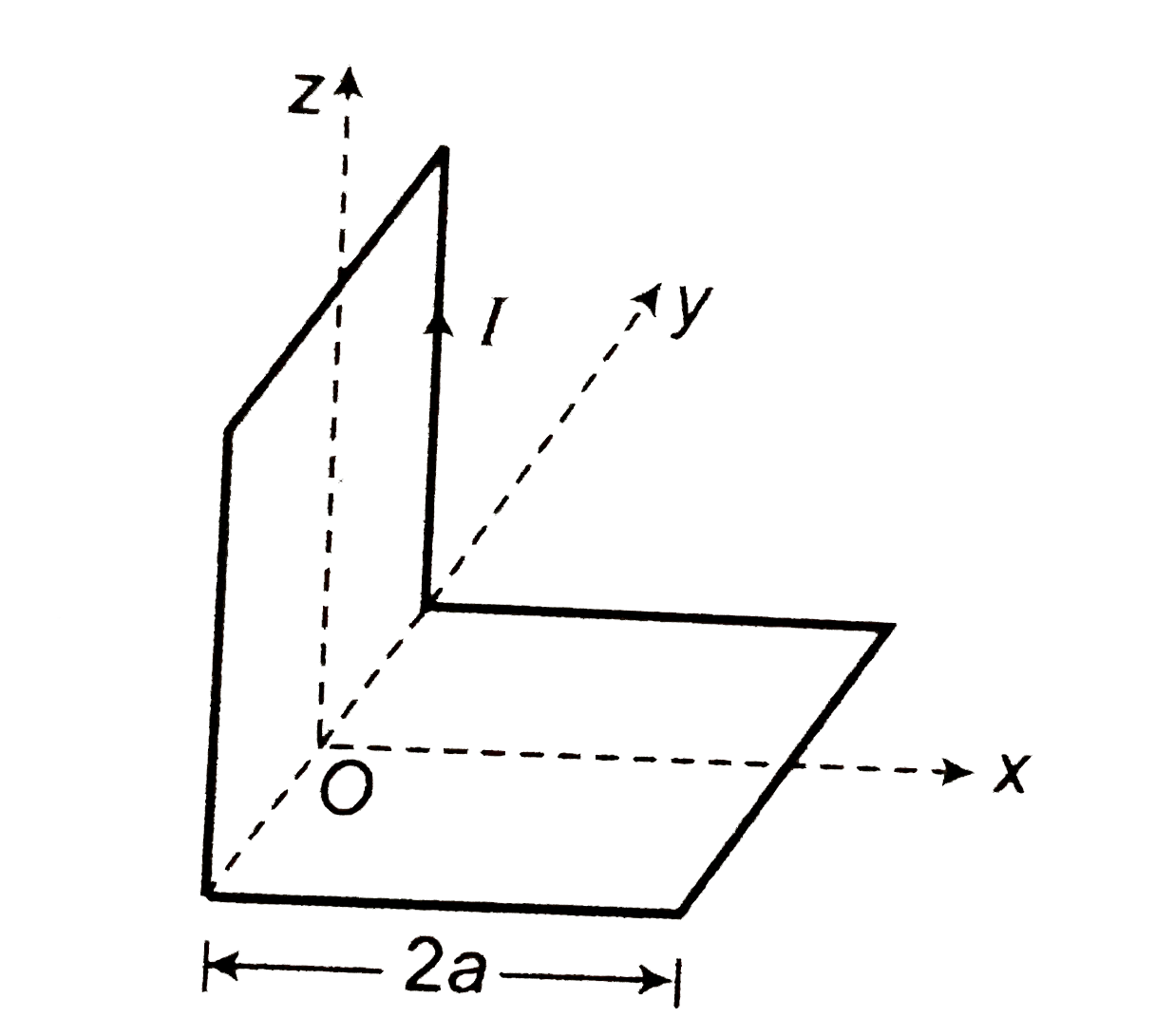
View SolutionA long, straight wire lies along the y-axis and carries a current I=8A in the y-direction (as shown in Fig) In addition to the magnetic field due to the current in the wire, a uniform magnetic field →B0 with magnitude 1.50×10−6T is in the +x direction. What is the total field (magnitude and direction ) at following points in the plane?
(a)x=0,z=1.00m
(b) x=1.00m,z=0
(c) x=0,z=−0.25m

View SolutionA long wire with a small current element of length 1 cm is placed at the origin and carries a current of 10 A along the X-axis. Find out the magnitude and direction of the magnetic field due to the element on the Y-axis at a distance 0.5 m from it.
View SolutionTwo infinitely long, thin, insulated, straight wires lie in the x-y plane along the x- and y- axis respectively. Each wire carries a current I, respectively in the positive x-direction and positive y-direction. The magnetic field will be zero at all points on the straight line:
View SolutionFigure. Shows two long wires carrying equal currents I1andI2 flowing in opposite directions. Which of the arrows labeled A to D correctely represents the direction of the magnetic field due to the wires at a point located at an equal distance d from each wire?
View Solution

