An infinitely long wire with a current I flowing in it is located in the boundary plane between two non-conducting media with permeabilities μ1 and μ2 . Find the modulus of the magnetic induction vector thorughout the space as a function of the distance r from the wire. It should be horne in mind that the lines of the vector B are circles whose centres lie on the axis of the wire.
The lines of the B as well as H field are circles around the wire. Thss
H1πr+H2πr=1 or, H1+H2=1πr
Also, μ0μ1H1=μ2H2μ0=B1=B2=B
Thus H1=μ2μ1+μ2Iπr
H2=μ1μ1+μ2Iπr
and B=μ0μ1μ2μ1+μ2Iπr,

Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field
36 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current
72 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Two inflinitely long wires carrying current I, are bent as shown in the figure. Find the magnetic induction at point C.
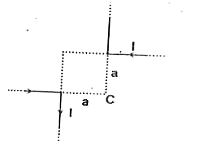
View SolutionA small conducting ball carrying a charge q is located in a uniform an infinite boundary plane between the dielectrics and vacumm. Find the surface density of the bound chagres on the boundary plane as a function of distance r from the ball. Analysse the obtained result for l→0.
View Solution
Knowledge Check
The magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
A|B|=(μ04π)2irB|B|=(μ04π)r2iC|B|=(4πμ0)2irD|B|=(4πμ0)r2iMagnetic field due to an infinite current carrying wire varies with the distance (r) from the wire as
ArBr2C1rD1r2one of the two infinitely long wires carrying current I is bent as shown in the adjacent figure. The magnetic induction at C is equal to
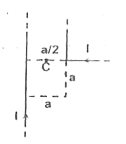 AzeroBμ0I2πaC3μ0I4πaDμ0Iπa
AzeroBμ0I2πaC3μ0I4πaDμ0Iπa
A current I flows in a long straight wire (into the plane of the paper) with cross-section having the from of a circular are of radius R a shown in the figure. Find the magnetic induction at the point O.
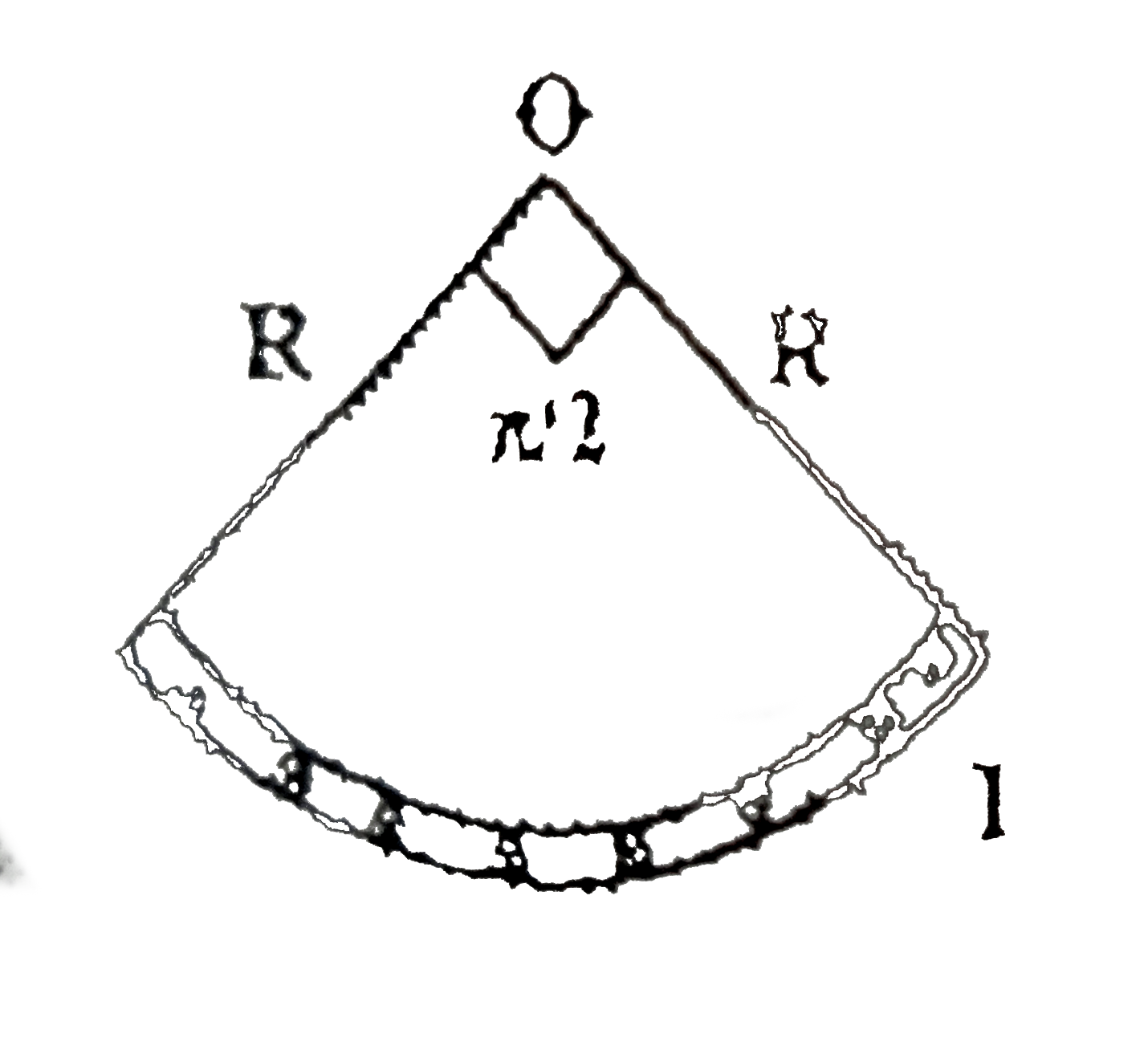
View SolutionA current I=IA flowing through an infinite long wire A1 divides between two infinite long wires A2 and A3 at junction B. The magnitude of the magnetic field at point O due to current through wires is :
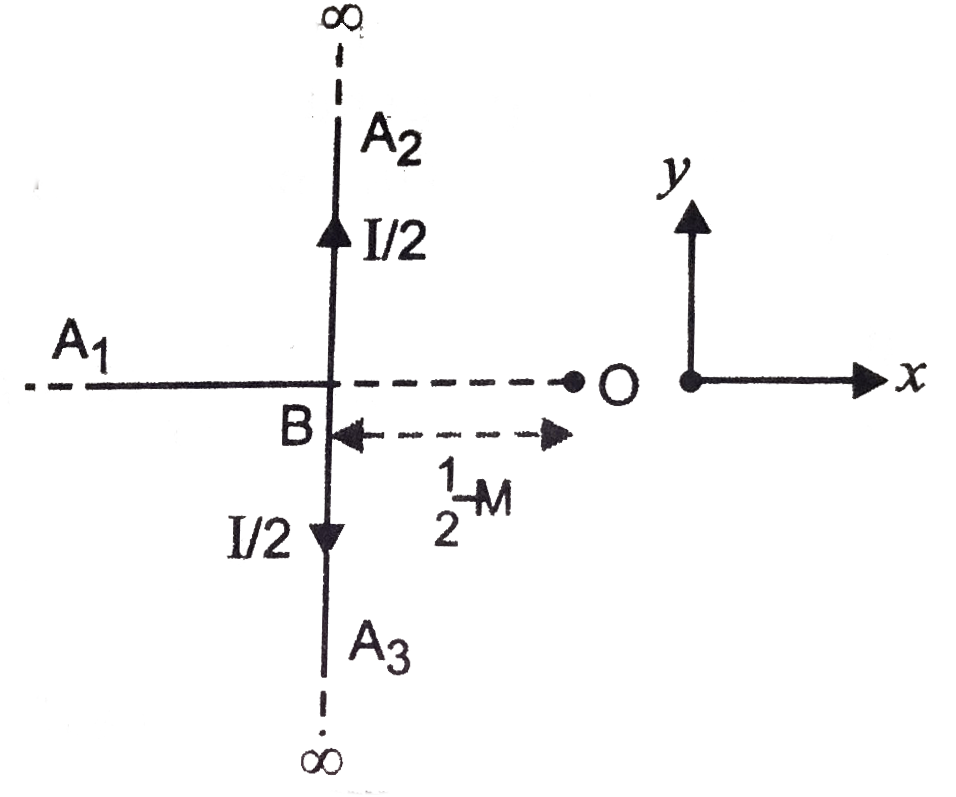
View SolutionA current 'I' flows along an infinitely long straight conductor. If 'r' is the perpendicular distance of a point from the lower end of the conductor, then the magnetic induction B is given by
View SolutionTwo infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
View SolutionA long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is
View Solution
