A round current-carrying loop lies in the plane boundary between magnetic and vacumm. The permeability of th emagnetic is equal to μ Find the magnetic induction B at an arbitary point on the axis of the loop if in the absence of th e magnetic the magnetic induction at the same point becomes equal to B0 . Genralize the obtained result to all poins of the field.
The medium I is vacumm and contains a circular current carrying coil with current I. The medium II is a megentic with permeabitliy μ. The boundary is the plane z=0 and the coil is the plane z=1. To find the magnitude induction we note that the effect of the magentic medium can be written as due to an image coil in II as far as the medim I is concerned. On the other hand, the induction is II as far as the medium I is concerned, On the other hand, the induction is II can be written as due t the coil in I, carrying a different current. It is sufficient to consider the far away fields and ensure that the boundary conditions are satisfied there. Now for actual coil in mediumI.

Br=−2pmcosθ'r3.(μ04π).B0=pmsinθ'r3(μ04π)
so, B2=μ0Pm4π(2cos2θ'−sin2θ') and Bx=μ0pm4π(−3sinθ'cosθ')
where pm=I(πa2),a = radius of the coil.
Similarly due to the image coil,
Bx=μ0p'4π(2cos2θ'−sin2θ),Bx=μ0p'4π(3sinθ'cosθ'),p'm=I'(πa2)
As fas as the medium II is concered, we write similarly
Bz=μ0p''m4π(2cos2−sin2θ'),Bx=μ0p''m4π(−3sinθ'cosθ').p''m=I''(πa2)
The boundary conditions are, pm+p'm=pm (from B1n−B2n)
pm+p'm=−1μpm (from H1t=H2t)
Thus, I=2μμ+1I,I'=μ−1μ+1I
In the limit, when the coil is on the boundary, the magnetic filed envery where can be obtained by taking the current to be 2μμ+1I. Thus, →B=2μμ+1−→B0
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electromagnetic Induction
84 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field
36 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current
72 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
Find the magnetic moment of a thin round loop with current if the radius of the loop is equal to R=100mm and the magnetic induction at its centre is equal to B=6.0μT.
View SolutionFind the magnetic moment of a thin round loop with current if the radius of the loop is equal to R=100mm and the magnetic induction at its centre is equal to B=6.0μT.
View Solution
Knowledge Check
In the loop shown, the magnetic induction at the point O
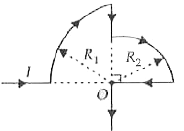 Aμ0I8(R1−R2R1R2)Bμ0I8(R1+R2R1R2)Cμ0I8(R1R2R1+R2)Dzero
Aμ0I8(R1−R2R1R2)Bμ0I8(R1+R2R1R2)Cμ0I8(R1R2R1+R2)DzeroIn the loop shown, the magnetic induction at the point 'o' is
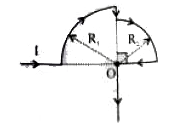 Aμ0I8(R1−R2R1R2)Bμ0I8(R1+R2R1R2)Cμ0I8(R1R2R1+R2)D0
Aμ0I8(R1−R2R1R2)Bμ0I8(R1+R2R1R2)Cμ0I8(R1R2R1+R2)D0The magnetic induction at a point on axis of a short magnetic dipole is
Aπ04π2Mr3Bπ04π3Mr31Cπ04πMr3Dπ04π2M2r3
Find the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
View SolutionFind the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
View SolutionFind the magnetic moment of a thin round loop with current if the radius of the loop is equal to r and the magnetic induction at its centre is equal to X.
View SolutionWhat is the magnetic moment of a current carrying thin circular loop if the radius of the loop is equal to R and the magnetic induction at its centre is equal to B ?
View SolutionMagnetic induction at a point due to short magnetic dipole isB1.The dipole is then cut into two equal parts.Magnetic induction at the same point due to either part is
View Solution
