An LR circuit having a time constant of 50 ms is connected with an ideal battery of emf ε . Find the time taken for the magnetic energy stored in the circuit to change from one fourth of the steady state value to half of the steady state value.
t=(LR)=50ms=0.05s
(a) i02=(i0)(1−e−t/0.03)
⇒(12)=1−e−t/0.03
⇒e−t/0.03=(12)
⇒Ine−t/0.03=In(14)
(take In both sides)
⇒t=0.05×0.693
=0.03465s
=34.6ms=35ms
(b)P=i2R=E2R(1−etR/L)2
MaξμmPower=E2R
so, (E^2)/(2R)=(E^2)/(R)(1-e^(tr/L)^2)<br>implies1-e^(-R//L)=(1)/(sqrt(2))=0.707<br>e^(-R//L)=0.293<br>implies t=50xx1.2275ms<br>=61.2ms .
Topper's Solved these Questions
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises89videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises75videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises9videos
ELECTROMAGNETIC WAVES
Similar Questions
An LR circuit having a time constant of 50 ms is connected with an ideal battery of emf ε . Find the time taken for the magnetic energy stored in the circuit to change from one fourth of the steady state value to half of the steady state value.
View SolutionAn LR circuit having a time constant of 50 ms is connected with an ideal battery of emf ε . Find the time taken for the magnetic energy stored in the circuti to change from one fourth of the steady state value to half of the steady stae value.
View Solution
Knowledge Check
- Question 1 - Select One
In a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
A(ln2)LRB0.5LRC√2LRD(√2√2−1)LR - Question 2 - Select One
In the circuit shown in fig.. Time constant and steady state current will be
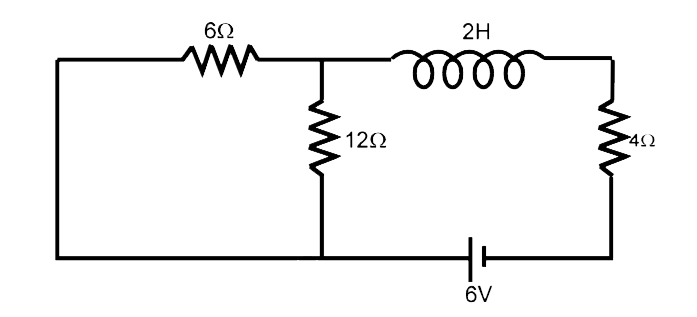 A0.25s,0.75AB0.75s,0.25AC0.25s,0.25AD0.5s,0.5A
A0.25s,0.75AB0.75s,0.25AC0.25s,0.25AD0.5s,0.5A
A coil having an inductance L and a resistance R is connected to a battery of emf E . Find the time taken for the magnetic energy stored in the circuit to change from one fourth of the steady-state value.
View SolutionA coil having an inductance L and a resistance R is connected to a battery of emfε. Find the time elapsed before, the magnetic field energy stored in the circuit reaches half its maximum value.
View SolutionIn a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
View SolutionFind the ratio between the energy stored in 5uF capacitor to the 4μF capacitor in the given circuit in steady state.
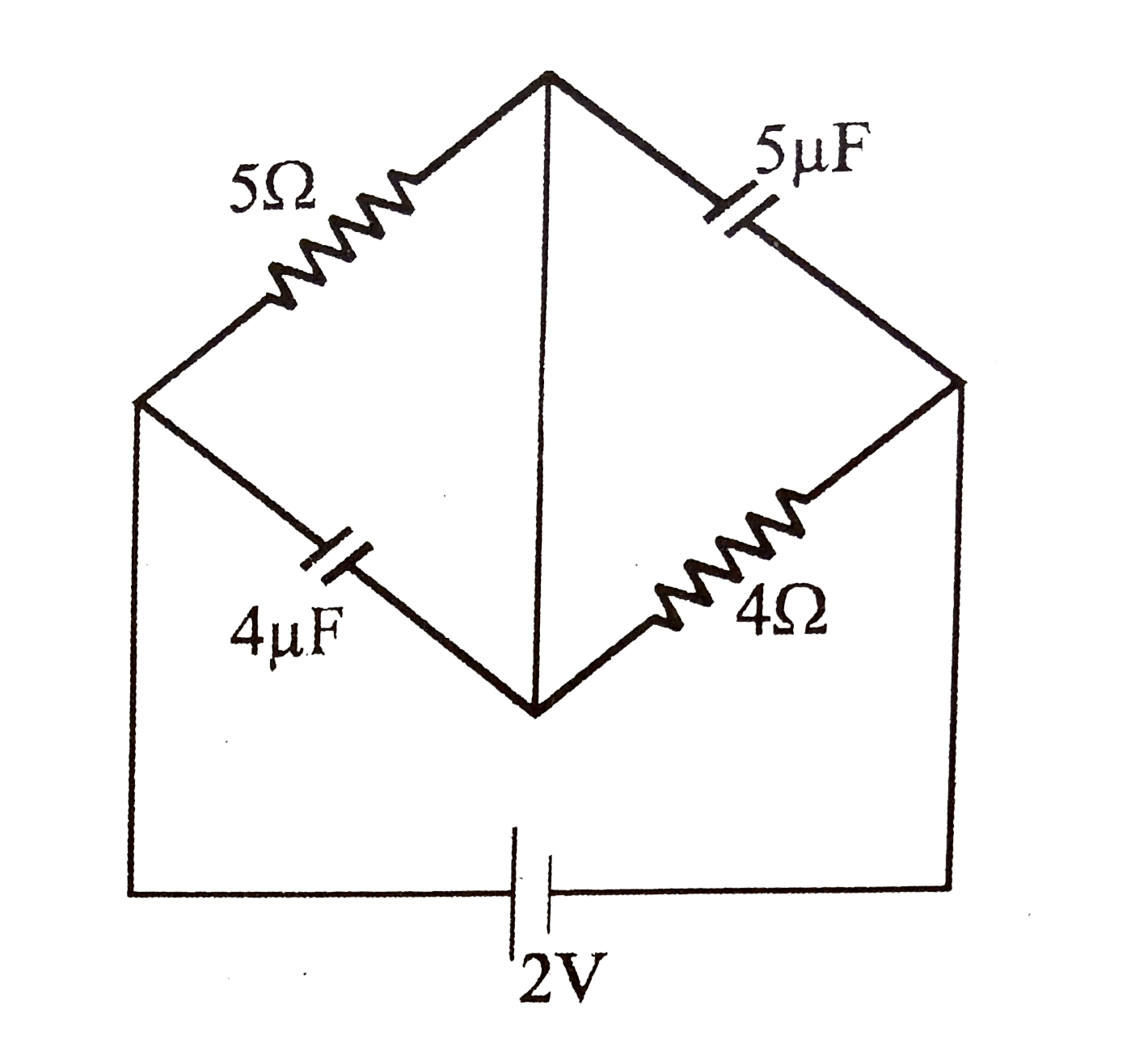 View Solution
View SolutionIn the circuit shown in figure, time constant and steady state current will be
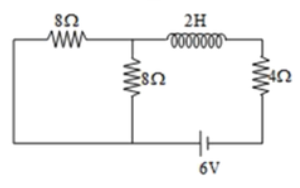 View Solution
View Solution
In the circuit shown in figure, time constant and steady state current will beView Solution

