An LR circuit having a time constant of 50 ms is connected with an ideal battery of emf ε . Find the time taken for the magnetic energy stored in the circuti to change from one fourth of the steady state value to half of the steady stae value.
To solve the problem of finding the time taken for the magnetic energy stored in an LR circuit to change from one-fourth of the steady-state value to half of the steady-state value, we can follow these steps:
Step 1: Understand the steady-state magnetic energy
The magnetic energy U stored in an inductor at steady state is given by the formula:
U=12LI2
where I is the steady-state current. The steady-state current I0 can be expressed as:
I0=ϵR
Thus, the steady-state magnetic energy becomes:
U0=12L(ϵR)2
Step 2: Determine the initial and final energy values
We need to find the time taken for the magnetic energy to change from one-fourth of the steady-state value to half of the steady-state value:
- Initial energy Ui=14U0
- Final energy Uf=12U0
Step 3: Relate magnetic energy to current
Using the expression for magnetic energy, we can relate the energy to the current:
U=12LI2
Setting Ui and Uf:
- For Ui:
14U0=12LI2i⟹I2i=U02⋅14=18U0⟹Ii=√18U0
- For Uf:
12U0=12LI2f⟹I2f=U0⟹If=√U0
Step 4: Use the current growth equation in an LR circuit
The current in an LR circuit as a function of time is given by:
I(t)=I0(1−e−tτ)
where τ=LR is the time constant.
Step 5: Set up equations for Ii and If
1. For Ii:
Ii=I0(1−e−t1τ)
2. For If:
If=I0(1−e−t2τ)
Step 6: Solve for t1 and t2
- For Ii=12I0:
12I0=I0(1−e−t1τ)⟹1−e−t1τ=12⟹e−t1τ=12
Taking the natural logarithm:
−t1τ=ln(12)⟹t1=−τln(12)
- For If=1√2I0:
1√2I0=I0(1−e−t2τ)⟹1−e−t2τ=1√2⟹e−t2τ=1−1√2
Taking the natural logarithm:
−t2τ=ln(1−1√2)⟹t2=−τln(1−1√2)
Step 7: Calculate the time difference t2−t1
The time taken for the magnetic energy to change from one-fourth to half of the steady-state value is:
Δt=t2−t1=−τ(ln(1−1√2)−ln(12))
Substituting τ=50ms:
Δt=−50ms(ln(1−1√2)−ln(12))
Step 8: Final calculation
Using the values:
- ln(1−1√2)≈−0.613
- ln(12)≈−0.693
Thus, we can compute:
Δt≈−50ms(−0.613+0.693)≈−50ms⋅0.08≈4ms
Final Answer:
The time taken for the magnetic energy stored in the circuit to change from one-fourth to half of the steady-state value is approximately 4 ms.
The magnetic energy U stored in an inductor at steady state is given by the formula:
U=12LI2
where I is the steady-state current. The steady-state current I0 can be expressed as:
I0=ϵR
Thus, the steady-state magnetic energy becomes:
U0=12L(ϵR)2
We need to find the time taken for the magnetic energy to change from one-fourth of the steady-state value to half of the steady-state value:
- Initial energy Ui=14U0
- Final energy Uf=12U0
Using the expression for magnetic energy, we can relate the energy to the current:
U=12LI2
Setting Ui and Uf:
- For Ui:
14U0=12LI2i⟹I2i=U02⋅14=18U0⟹Ii=√18U0
- For Uf:
12U0=12LI2f⟹I2f=U0⟹If=√U0
The current in an LR circuit as a function of time is given by:
I(t)=I0(1−e−tτ)
where τ=LR is the time constant.
1. For Ii:
Ii=I0(1−e−t1τ)
2. For If:
If=I0(1−e−t2τ)
- For Ii=12I0:
12I0=I0(1−e−t1τ)⟹1−e−t1τ=12⟹e−t1τ=12
Taking the natural logarithm:
−t1τ=ln(12)⟹t1=−τln(12)
1√2I0=I0(1−e−t2τ)⟹1−e−t2τ=1√2⟹e−t2τ=1−1√2
Taking the natural logarithm:
−t2τ=ln(1−1√2)⟹t2=−τln(1−1√2)
The time taken for the magnetic energy to change from one-fourth to half of the steady-state value is:
Δt=t2−t1=−τ(ln(1−1√2)−ln(12))
Substituting τ=50ms:
Δt=−50ms(ln(1−1√2)−ln(12))
Using the values:
- ln(1−1√2)≈−0.613
- ln(12)≈−0.693
Δt≈−50ms(−0.613+0.693)≈−50ms⋅0.08≈4ms
The time taken for the magnetic energy stored in the circuit to change from one-fourth to half of the steady-state value is approximately 4 ms.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 27videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
Similar Questions
A coil having an inductance L and a resistance R is connected to a battery of emfε. Find the time elapsed before, the magnetic field energy stored in the circuit reaches half its maximum value.
View SolutionIn a decaying L−R circuit, the time after which energy stores in the inductor reduces to one fourth of its initial values is
View SolutionA capacitor of capacitance C is connected to a battery of emf (ε)at t=0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate has this maximum value?
View SolutionFour resistance are connected by an ideal battery of emf 50 volt, circuit is in steady state then the current in wire AB is :
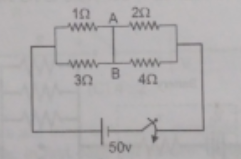 View Solution
View SolutionAn inductor coil carries a steady state current of 2.0 A when connected across an ideal battery of emf 4.0 V. if its inductance is 1.0 H, find the time constant of the circuit.
View SolutionThe capacitor shown in the figure is initially unchanged, the battery is ideal. The switch S is closed at time t= 0, then the time after which the energy stored in the capacitor becomes one - fourth of the energy stored in it in steady - state is :
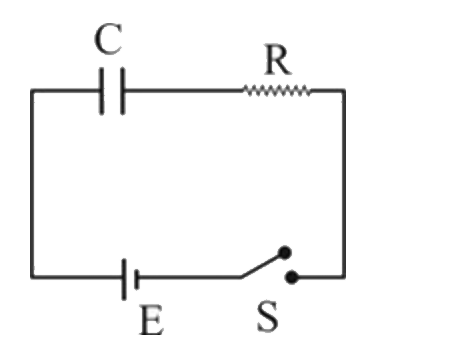 View Solution
View SolutionA coil of inductance 1.0 H and resistance 100 Omega is connected to a battery of emf 12 V. Find the energy stored in the magnetic field associated with the coil at an instant 10 ms after the circuit is switched on.
View SolutionA coil of inductance 1H and resistance 10Ω is connected to a resistanceless battery of emf 50V at time t=0. Calculate the ratio of rthe rate which magnetic energy is stored in the coil to the rate at which energy is supplied by the battery at t=0.1s.
View SolutionA solenoid of inductance 50 mH and resistance 10 Omega is connected to a battery of 6V. Find the time elapsed before the current acquires half of its steady - stae value.
View SolutionAn inductor having self inductance L with its coil resistance R is connected across a battery of emf ε. When the circuit is in steady state t = 0, an iron rod is inserted into the inductor due to which its inductance becomes nL(n>1).
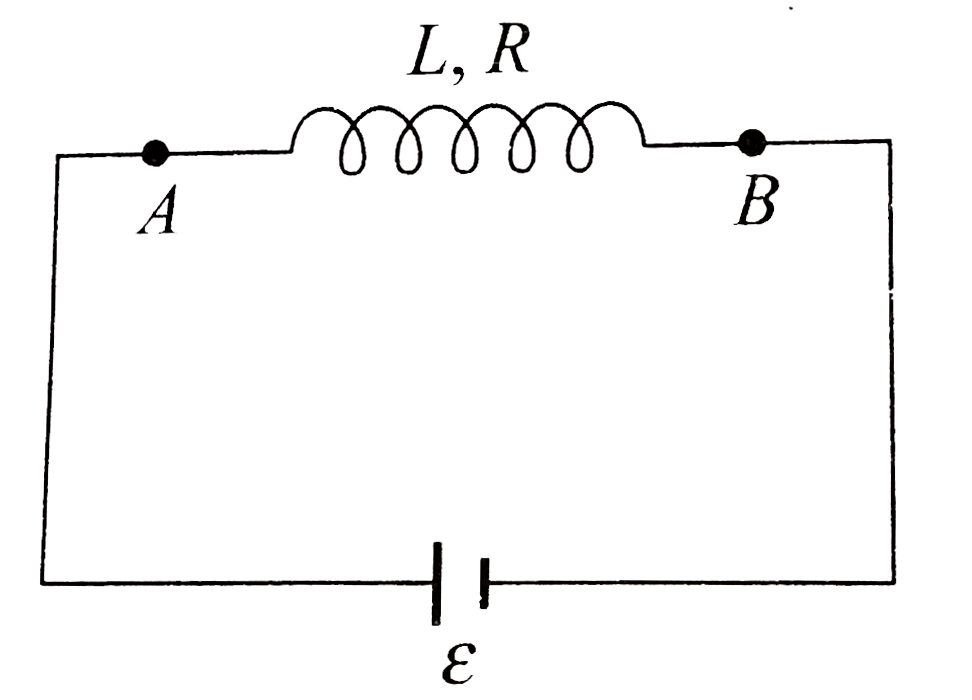
When again circuit is in steady state, the current in it isView Solution

