An O16 nucleus is spherical and has a radius R and a volume V=43πR3.According to the empirical observation, the volume of the .54X128 nucleus assumed to be sphericla is V' and radius is R'. Then
V'=8V
V'=2V
R'=2R
R'=8R
The correct Answer is:a,c
To solve the problem, we need to analyze the relationship between the radius and volume of the nuclei based on their mass numbers.
1. Understanding the Volume of a Nucleus:
The volume V of a spherical nucleus is given by the formula:
V=43πR3
where R is the radius of the nucleus.
2. Relating Radius to Mass Number:
According to empirical observations, the radius R of a nucleus can be expressed as:
R=R0A1/3
where R0 is a constant and A is the mass number of the nucleus.
3. Calculating the Radius for O16:
For the oxygen-16 nucleus (O16), the mass number A=16:
R=R0(16)1/3
4. Calculating the Radius for X128:
For the nucleus X128 with mass number A=128:
R′=R0(128)1/3
5. Finding the Ratio of Radii:
We can find the ratio of the radii R′ and R:
R′R=R0(128)1/3R0(16)1/3=(128)1/3(16)1/3=(12816)1/3=(8)1/3=2
Therefore, we have:
R′=2R
6. Finding the Volume Ratio:
Now, we can find the ratio of the volumes V′ and V:
V′=43π(R′)3=43π(2R)3=43π(8R3)=8(43πR3)=8V
Thus, we have:
V′=8V
Conclusion:
From our calculations, we find that:
- The radius of nucleus X128 is R′=2R.
- The volume of nucleus X128 is V′=8V.
Correct Options:
- V′=8V (Option A)
- R′=2R (Option C)
The volume V of a spherical nucleus is given by the formula:
V=43πR3
where R is the radius of the nucleus.
According to empirical observations, the radius R of a nucleus can be expressed as:
R=R0A1/3
where R0 is a constant and A is the mass number of the nucleus.
For the oxygen-16 nucleus (O16), the mass number A=16:
R=R0(16)1/3
For the nucleus X128 with mass number A=128:
R′=R0(128)1/3
We can find the ratio of the radii R′ and R:
R′R=R0(128)1/3R0(16)1/3=(128)1/3(16)1/3=(12816)1/3=(8)1/3=2
Therefore, we have:
R′=2R
Now, we can find the ratio of the volumes V′ and V:
V′=43π(R′)3=43π(2R)3=43π(8R3)=8(43πR3)=8V
Thus, we have:
V′=8V
From our calculations, we find that:
- The radius of nucleus X128 is R′=2R.
- The volume of nucleus X128 is V′=8V.
- V′=8V (Option A)
- R′=2R (Option C)
Topper's Solved these Questions
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Linked Comprehension
29 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Integer
6 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Subjective
35 Videos
- MISCELLANEOUS VOLUME 5BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer
12 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer Type
4 Videos
Similar Questions
If a sphere of radius 2r has the same volume as that of a cone with circular base of radius r, then find the height of the cone.
View SolutionThe nuclear charge (Ze) is non uniformlly distribute with in a nucleus of radius r. The charge densilty ρ(r) (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
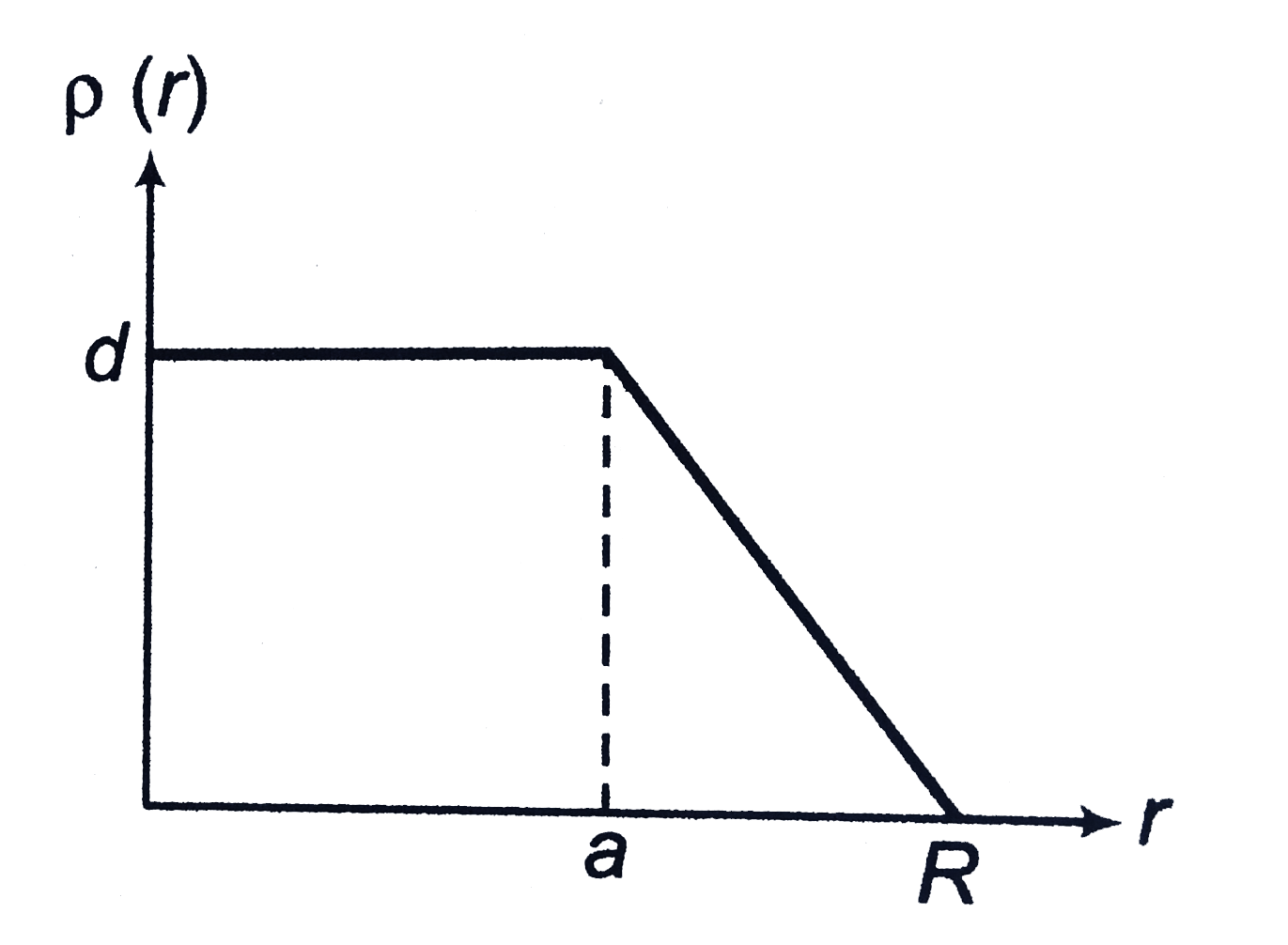
The electric field within the nucleus is generaly observed to be linearly dependent on r. This implies
View SolutionUsing the method of integration, show that the volume of a right circular cone of base radius r and height h is V=13πr2h.
View SolutionThe nuclear charge (Ze) is non uniformlly distribute with in a nucleus of radius r. The charge densilty ρ(r) (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.

The electric field within the nucleus is generaly observed to be linearly dependent on r. This implies
View SolutionThe nucleus and an atom can be assumed to be spherical. The radius of atom is on Å if the mass number is 64, the fraction fo the atomic volume that is occupied by the nucleus is:
View SolutionRadius of .42HeThe nucleus is 3 Fermi. The radius of .3216S nucleus will be
View SolutionIf the height and radius of a cone of volume V are doubled, then the volume of the cone, is (a) 3 V (b) 4 V (c) 6 V (d) 8 V
View SolutionThe electrostatic energy of Z protons uniformly distributed throughout a spherical nucleus of radius R is given by
E=3Z(Z−1)e25(4πe0R)
The measured masses of the neutron _(1)1H,157Nand,168Oare1.008665u,1.007825u,15.000109uand15.003065u, respectively Given that the ratio of both the _(7)12N and _(8)15O nucleus are same , 1 u = = 931.5 Me Vc2 (c is the speed of light ) and e2/(4πe0)=1.44MeV fm Assuming that the difference between the binding energies of _715Nand_(8)^(15) O is purely due to the electric energy , The radius of the nucleus of the nuclei is
View SolutionFigure shows a hemispherical shell of mass M and radius R and a concentric shell of mass m and radius 3R/4.

View SolutionTwo soap bubbles with radius 2r and 3r come in contact. Their common surface has a radius of curvature nr, then find the value of n
View Solution
