An object is approaching a fixed plane mirror with velocity 5ms−1 making an angle of 45∘ with the normal. The speed of image w.r.t. the mirror is
5ms−1
5/√2ms−1
5√2ms−1
10ms−1
The correct Answer is:a.
To solve the problem of finding the speed of the image with respect to the mirror when an object approaches a fixed plane mirror at an angle, we can follow these steps:
1. Identify Given Data:
- Velocity of the object, vo=5m/s
- Angle with the normal, θ=45∘
2. Resolve the Velocity into Components:
- The object's velocity can be resolved into two components:
- Perpendicular Component (towards the mirror):
vo⊥=vocos(θ)=5cos(45∘)=5×1√2=5√2m/s
- Parallel Component (along the mirror):
vo∥=vosin(θ)=5sin(45∘)=5×1√2=5√2m/s
3. Calculate the Speed of the Image:
- The image in a plane mirror moves with the same speed as the object but in the opposite direction. Therefore, the speed of the image vi with respect to the mirror is:
- The perpendicular component doubles because the image moves away from the mirror as the object approaches:
vi⊥=2vo⊥=2×5√2=10√2m/s
- The parallel component remains the same:
vi∥=vo∥=5√2m/s
4. Calculate the Resultant Speed of the Image:
- The resultant speed of the image with respect to the mirror can be calculated using the Pythagorean theorem:
vi=√(vi⊥)2+(vi∥)2
vi=
⎷(10√2)2+(5√2)2
vi=√1002+252=√1252=√62.5≈7.91m/s
Final Answer:
The speed of the image with respect to the mirror is approximately 7.91m/s.
- Velocity of the object, vo=5m/s
- Angle with the normal, θ=45∘
- The object's velocity can be resolved into two components:
- Perpendicular Component (towards the mirror):
vo⊥=vocos(θ)=5cos(45∘)=5×1√2=5√2m/s
- Parallel Component (along the mirror):
vo∥=vosin(θ)=5sin(45∘)=5×1√2=5√2m/s
- The image in a plane mirror moves with the same speed as the object but in the opposite direction. Therefore, the speed of the image vi with respect to the mirror is:
- The perpendicular component doubles because the image moves away from the mirror as the object approaches:
vi⊥=2vo⊥=2×5√2=10√2m/s
- The parallel component remains the same:
vi∥=vo∥=5√2m/s
- The resultant speed of the image with respect to the mirror can be calculated using the Pythagorean theorem:
vi=√(vi⊥)2+(vi∥)2
vi=
⎷(10√2)2+(5√2)2
vi=√1002+252=√1252=√62.5≈7.91m/s
The speed of the image with respect to the mirror is approximately 7.91m/s.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension51videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective26videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
An object is approaching a fixed plane mirror with velocity 3 ms/s at an angle of 45∘ with normal, in a medium of refractive index 4/3. The speed of the image with respect to the mirror is __________m/s.
View SolutionFill in the Blanks
Q An object is kept symmetrically between two plane mirrors making an angle of 40° between them. The number of images of the object in the mirrors is…...................View SolutionA real object is moving toward a fixed spherical mirror. The image
View SolutionA linear object AB is placed along the axis of a concave mirror. This object is moving towards the mirror with speed U. The speed of the image of the point A is 4U and the speed of the image of B is alSO 4U btu in opposite direction. If the center of the line AB is at a distance L from the mirror then find out the length of the object.
 View Solution
View SolutionAn object is moving towards a mirror with a velocity of 10ms−1 as shown in the figure. If the collision between the mirror and the object is perfectly elastic, then the velocity of the image after collision with mirror in vector form is
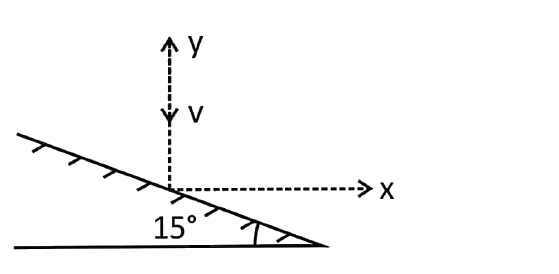 View Solution
View SolutionImages formed by an object placed between two plane mirrors whose reflecting surfaces make an angle of 90∘with one another lie on a:
View SolutionAn object is placed asymmetrically between two plane mirrors inclined at an angle of 72∘. The number of images formed is
View SolutionA point object O and a mirror M move with velocities of 3cms−1 and 4cms−1 , respectively as shown in the figure. OO' is the normal to the mirror. What is the velocity of the image?
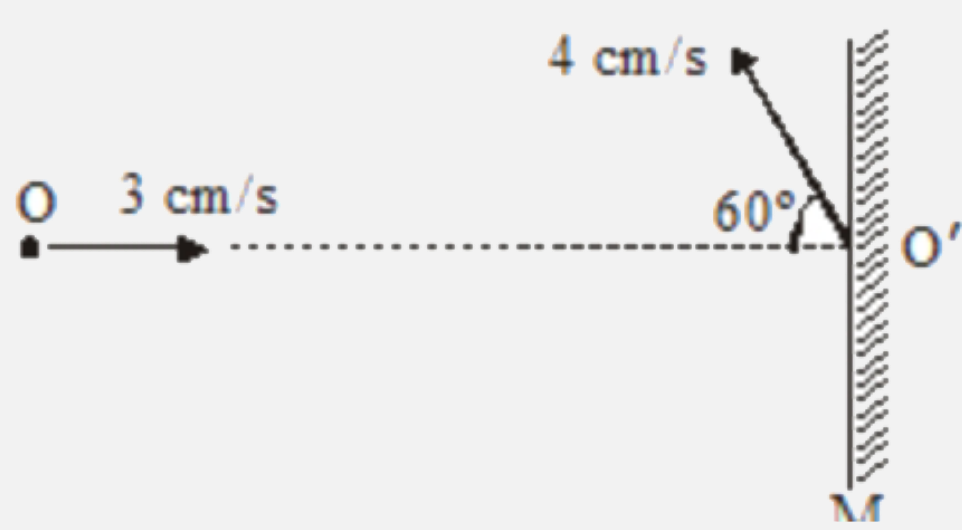 View Solution
View SolutionAn object placed in front of a plane mirror is displaced by 0.4 m along a straight line at an angle of 30∘ to mirror plane. The change in the distance between the object and its image is:
View SolutionThe mirror are inclined at angle of 50∘. The number of images formed for an object placed in between the mirrors is
View Solution

