An object of mass 3 kg is at rest . Now a force F=6t2ˆi+2tˆj is applied on the object . Find the velocity of the object at t =3 sec.
To solve the problem step by step, we will follow these steps:
Step 1: Identify the given values
- Mass of the object, m=3kg
- Force applied, F=6t2^i+2t^j
Step 2: Calculate the acceleration
Using Newton's second law, we know that:
F=m⋅a
Thus, the acceleration a can be calculated as:
a=Fm=6t2^i+2t^j3
This simplifies to:
a=2t2^i+23t^j
Step 3: Integrate acceleration to find velocity
Since velocity is the integral of acceleration, we will integrate the components of acceleration with respect to time t.
For the x-component of velocity vx:
vx=∫axdt=∫2t2dt=23t3+Cx
Since the object starts from rest, the initial velocity vx(0)=0:
Cx=0⟹vx=23t3
For the y-component of velocity vy:
vy=∫aydt=∫23tdt=13t2+Cy
Again, since the object starts from rest, the initial velocity vy(0)=0:
Cy=0⟹vy=13t2
Step 4: Calculate the velocity at t=3s
Now we can substitute t=3 seconds into the equations for vx and vy.
For vx:
vx(3)=23(3)3=23×27=18m/s
For vy:
vy(3)=13(3)2=13×9=3m/s
Step 5: Combine the components to find the velocity vector
The velocity vector at t=3s is:
v=vx^i+vy^j=18^i+3^jm/s
Step 6: Calculate the magnitude of the velocity
The magnitude of the velocity vector can be calculated as:
|v|=√(vx)2+(vy)2=√(18)2+(3)2=√324+9=√333≈18.25m/s
Final Answer
The velocity of the object at t=3s is:
v=18^i+3^jm/sand its magnitude is approximately 18.25m/s.
---
- Mass of the object, m=3kg
- Force applied, F=6t2^i+2t^j
Using Newton's second law, we know that:
F=m⋅a
Thus, the acceleration a can be calculated as:
a=Fm=6t2^i+2t^j3
This simplifies to:
a=2t2^i+23t^j
Since velocity is the integral of acceleration, we will integrate the components of acceleration with respect to time t.
vx=∫axdt=∫2t2dt=23t3+Cx
Since the object starts from rest, the initial velocity vx(0)=0:
Cx=0⟹vx=23t3
vy=∫aydt=∫23tdt=13t2+Cy
Again, since the object starts from rest, the initial velocity vy(0)=0:
Cy=0⟹vy=13t2
Now we can substitute t=3 seconds into the equations for vx and vy.
vx(3)=23(3)3=23×27=18m/s
vy(3)=13(3)2=13×9=3m/s
The velocity vector at t=3s is:
v=vx^i+vy^j=18^i+3^jm/s
The magnitude of the velocity vector can be calculated as:
|v|=√(vx)2+(vy)2=√(18)2+(3)2=√324+9=√333≈18.25m/s
The velocity of the object at t=3s is:
v=18^i+3^jm/sand its magnitude is approximately 18.25m/s.
Similar Questions
An object of mass 3kg is at rest. Now a force of →F=6t2ˆi+4tˆj is applied on the object, the velocity of object at t=3s is.
View SolutionAn object of mass 3kg is at rest. Now a force of →F=6t2ˆI+4tˆj is applied on the object, the velocity of object at t=3s is.
View SolutionAn object of mass 3kg is at rest. Now a force of →F=6t2ˆI+4tˆj is applied on the object, the velocity of object at t=3s is.
View SolutionIn the given x - t graph. Find the position of an object at t = 3 second

View SolutionAn object of mass 2 kg at rest at origin starts moving under the action of a force
→F=(3t2ˆi+4tˆj)N The velocity of the object at t = 2 s will be -
View SolutionThe position of a particle is expressed as →r=(4t2ˆi+2tˆj) m, where t is time in second. Find the velocity o the particle at t = 3 s
View SolutionAn object of mass 5 kg is acted upon by a force that varies with position of the object as shown. If the object starts out from rest at a point x=0. What is its speed at x=50 m.
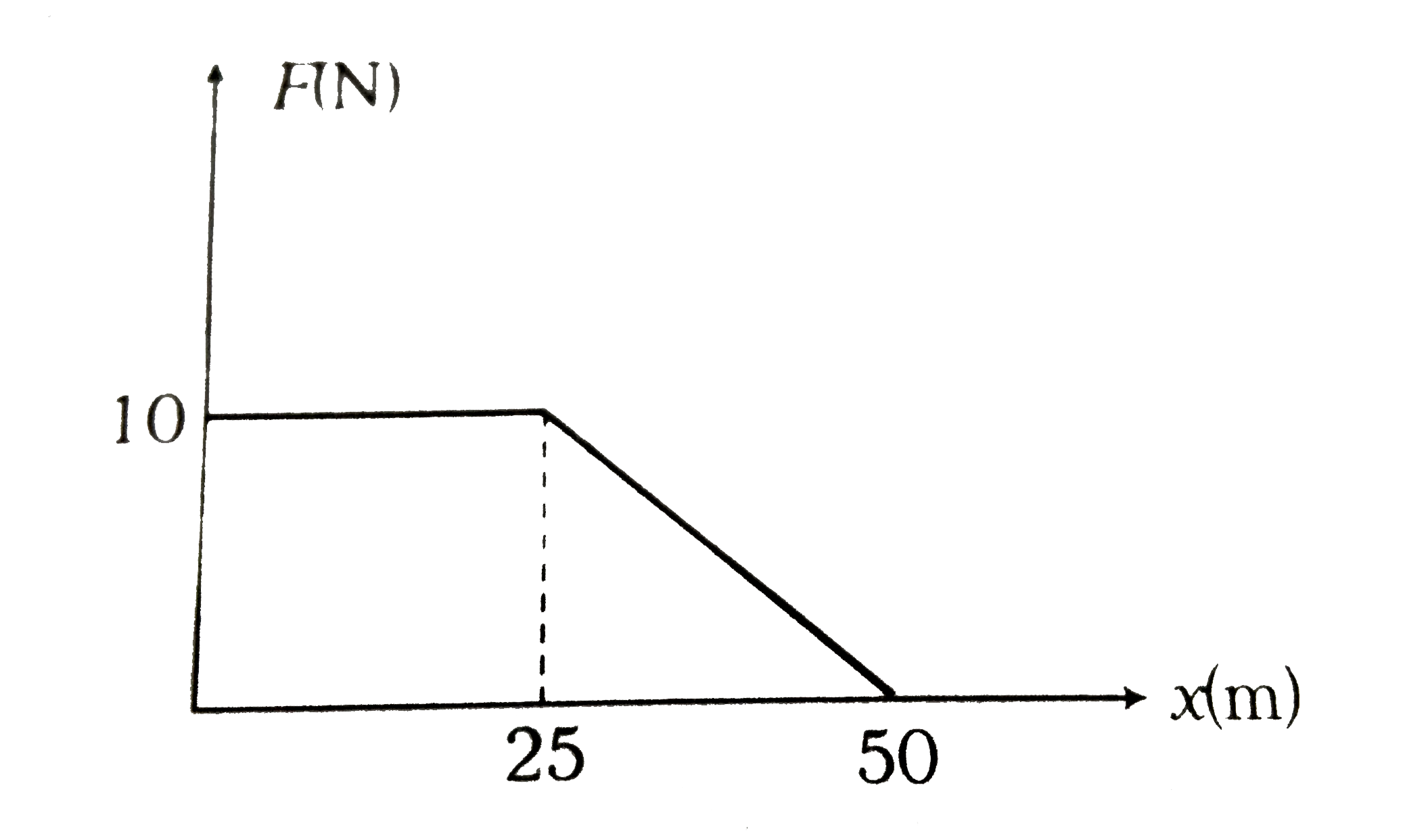
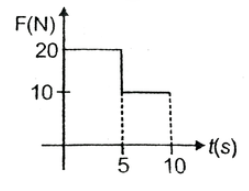
View SolutionForce is applied on an object of mass 2 kg at rest on a frictionless horizontal surface as shown in the graph. The speed of object at t=10 s will be
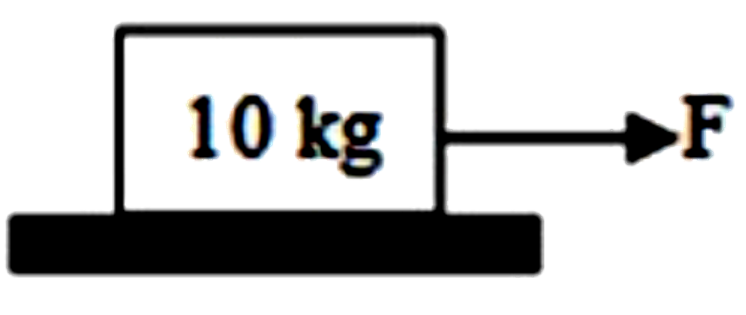
View SolutionA force F=2t2 is applied to the cart of mass 10 Kg, initially at rest. The speed of the cart at t = 5 s is -
View SolutionThe displacement of an object of mass 3 kg is given by the relation S=13t2, where t is time in seconds. If the work done by the net force on the object in 2 s is pq joule, where p and q are smallest integer values, then what is the value of p+q?
View Solution
