An object of mass m is allowed to fall from rest along a rough inclined plane. The speed of the object on reaching the bottom of the plane is proportional to:
m0
m
m2
m−1
The correct Answer is:A
To determine the speed of an object of mass m falling from rest along a rough inclined plane, we can use the principles of energy and the work-energy theorem. Here’s a step-by-step solution:
Step 1: Identify the forces acting on the object
When the object is on the inclined plane, the forces acting on it are:
- The gravitational force, mg, acting downwards.
- The normal force, N, acting perpendicular to the surface of the incline.
- The frictional force, Ff, acting opposite to the direction of motion.
Step 2: Resolve the gravitational force
The gravitational force can be resolved into two components:
- Perpendicular to the incline: N=mgcos(θ)
- Parallel to the incline: Fparallel=mgsin(θ)
Step 3: Determine the frictional force
The frictional force can be expressed as:
Ff=μN=μmgcos(θ)
where μ is the coefficient of friction.
Step 4: Apply the work-energy theorem
According to the work-energy theorem:
Work done by net force=Change in kinetic energy
The work done by the gravitational force and the frictional force can be expressed as:
Work done by gravity−Work done by friction=ΔKE
Step 5: Calculate the work done
The height of the incline is h, and the length of the incline can be expressed in terms of height and angle:
r=hsin(θ)
The work done by gravity is:
Wg=mgh
The work done against friction is:
Wf=Ff⋅r=μmgcos(θ)⋅hsin(θ)=μmghcot(θ)
Step 6: Set up the equation
Now, we can set up the equation:
mgh−μmghcot(θ)=12mv2
Step 7: Simplify the equation
We can cancel m from both sides (assuming m≠0):
gh−μghcot(θ)=12v2
Step 8: Solve for v2
Rearranging gives:
v2=2gh(1−μcot(θ))
Step 9: Find the speed v
Taking the square root gives:
v=√2gh(1−μcot(θ))
Conclusion
The speed of the object on reaching the bottom of the inclined plane is proportional to:
√h
since the other factors are constants or depend on the angle and friction.
When the object is on the inclined plane, the forces acting on it are:
- The gravitational force, mg, acting downwards.
- The normal force, N, acting perpendicular to the surface of the incline.
- The frictional force, Ff, acting opposite to the direction of motion.
The gravitational force can be resolved into two components:
- Perpendicular to the incline: N=mgcos(θ)
- Parallel to the incline: Fparallel=mgsin(θ)
The frictional force can be expressed as:
Ff=μN=μmgcos(θ)
where μ is the coefficient of friction.
According to the work-energy theorem:
Work done by net force=Change in kinetic energy
The work done by the gravitational force and the frictional force can be expressed as:
Work done by gravity−Work done by friction=ΔKE
The height of the incline is h, and the length of the incline can be expressed in terms of height and angle:
r=hsin(θ)
The work done by gravity is:
Wg=mgh
The work done against friction is:
Wf=Ff⋅r=μmgcos(θ)⋅hsin(θ)=μmghcot(θ)
Now, we can set up the equation:
mgh−μmghcot(θ)=12mv2
We can cancel m from both sides (assuming m≠0):
gh−μghcot(θ)=12v2
Rearranging gives:
v2=2gh(1−μcot(θ))
Taking the square root gives:
v=√2gh(1−μcot(θ))
The speed of the object on reaching the bottom of the inclined plane is proportional to:
√h
since the other factors are constants or depend on the angle and friction.
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - A Only One Option is Correct
42 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
Three different objects of masses m1,m2 and m2 are allowed to fall from rest and from the same point O along three different frictionless paths. The speeds of three objects on reaching the ground will be:
View SolutionA disc of mass 3 kg rolls down an inclined plane of height 5 m. The translational kinetic energy of the disc on reaching the bottom of the inclined plane is
View Solution
Knowledge Check
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
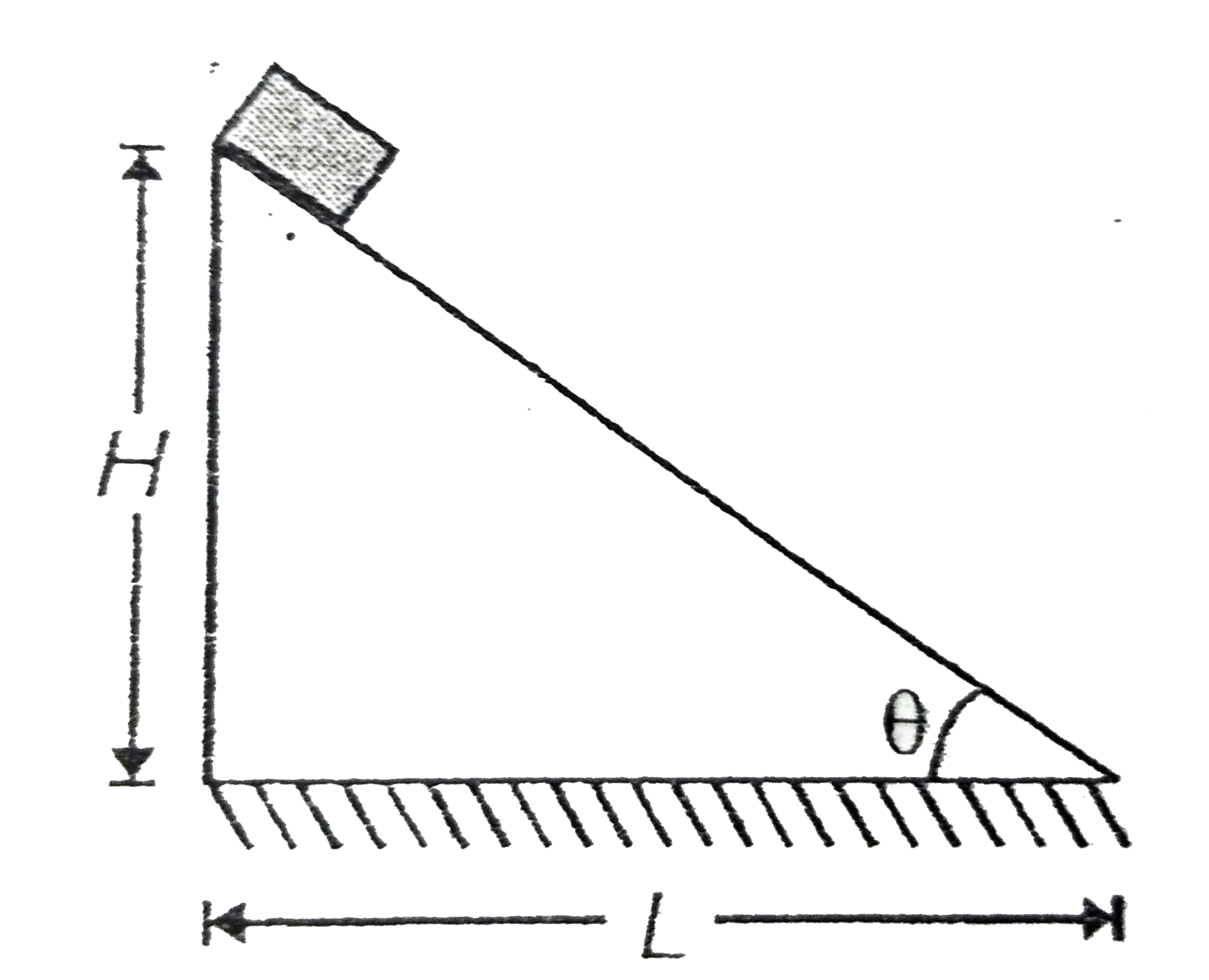
View SolutionA block of mass 4kg is released from the top of a rough inclines plane of height 10m. If velocity of the block is10m/s at the bottom of the inclined then work done by the friction force on the block will be
View SolutionSTATEMENT-1 : Two disks having same radius but different masses roll down without slipping from rest, on a rough inclined plane. They will take the same time to reach the bottom.
and
STATEMENT-2 : The heavier disc will have greater kinetic energy than the lighter disc, at the bottom.
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h. The angular velocity of the cylinder when it reaches the bottom of the plane will be :
View SolutionA body weighs 64 N on the surface of the Earth. What is the gravitational force on it (in N) due to the Earth at a height equal to one-third of the radius of the Earth?
View SolutionAn object is placed on the surface of a smooth inclined plane of inclination θ . It takes time t to reach the bottom of the inclined plane. If the same object is allowed to slide down rough inclined plane of same inclination θ, it takes time nt to reach the bottom where n is a number greater than 1. The coefficient of friction μ is given by -
View Solution
