A block of mass 4kg is released from the top of a rough inclines plane of height 10m. If velocity of the block is10m/s at the bottom of the inclined then work done by the friction force on the block will be
+200J
+100J
−200J
−100J
To find the work done by the friction force on a block of mass 4 kg released from a height of 10 m on a rough inclined plane, we can follow these steps:
Step 1: Calculate the initial potential energy (PE_initial)
The potential energy at the top of the incline can be calculated using the formula:
PEinitial=m⋅g⋅h
Where:
- m=4kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
- h=10m (height)
Substituting the values:
PEinitial=4⋅10⋅10=400J
Step 2: Calculate the final kinetic energy (KE_final)
The kinetic energy at the bottom of the incline can be calculated using the formula:
KEfinal=12mv2
Where:
- v=10m/s (velocity at the bottom)
Substituting the values:
KEfinal=12⋅4⋅(10)2=12⋅4⋅100=200J
Step 3: Determine the work done by friction
The work done by friction can be found by comparing the initial potential energy and the final kinetic energy. The work done by friction (W_friction) is the difference between the initial potential energy and the final kinetic energy:
Wfriction=KEfinal−PEinitial
Substituting the values:
Wfriction=200J−400J=−200J
Step 4: Interpret the result
The negative sign indicates that the work done by friction is in the opposite direction to the motion of the block. Therefore, the work done by the friction force is:
Wfriction=−200J
Conclusion
The work done by the friction force on the block is −200J.
---
The potential energy at the top of the incline can be calculated using the formula:
PEinitial=m⋅g⋅h
Where:
- m=4kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
- h=10m (height)
PEinitial=4⋅10⋅10=400J
The kinetic energy at the bottom of the incline can be calculated using the formula:
KEfinal=12mv2
Where:
- v=10m/s (velocity at the bottom)
KEfinal=12⋅4⋅(10)2=12⋅4⋅100=200J
The work done by friction can be found by comparing the initial potential energy and the final kinetic energy. The work done by friction (W_friction) is the difference between the initial potential energy and the final kinetic energy:
Wfriction=KEfinal−PEinitial
Substituting the values:
Wfriction=200J−400J=−200J
The negative sign indicates that the work done by friction is in the opposite direction to the motion of the block. Therefore, the work done by the friction force is:
Wfriction=−200J
The work done by the friction force on the block is −200J.
Similar Questions
Knowledge Check
A block mass 3 kg slides down a frictionless inclined plane of length 6 m and height 4 m. if the block is released from rest at the top of the incline, what is its speed at the bottom?
A5m/sB6m/sC8m/sD9m/sA block of mass 3 kg rests on a rough inclined plane making an angle of 30∘. With the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8 NB0.7×9.8×√3 NC9.8×√3 ND0.7×9.8 NA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3N
A block of mass 1 kg slides down a rough inclined plane of inclination 60∘ starting from its top. If coefficient of kinetic is 0.5 and length of the plane d=2 m, then work done against friction is
View SolutionA small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
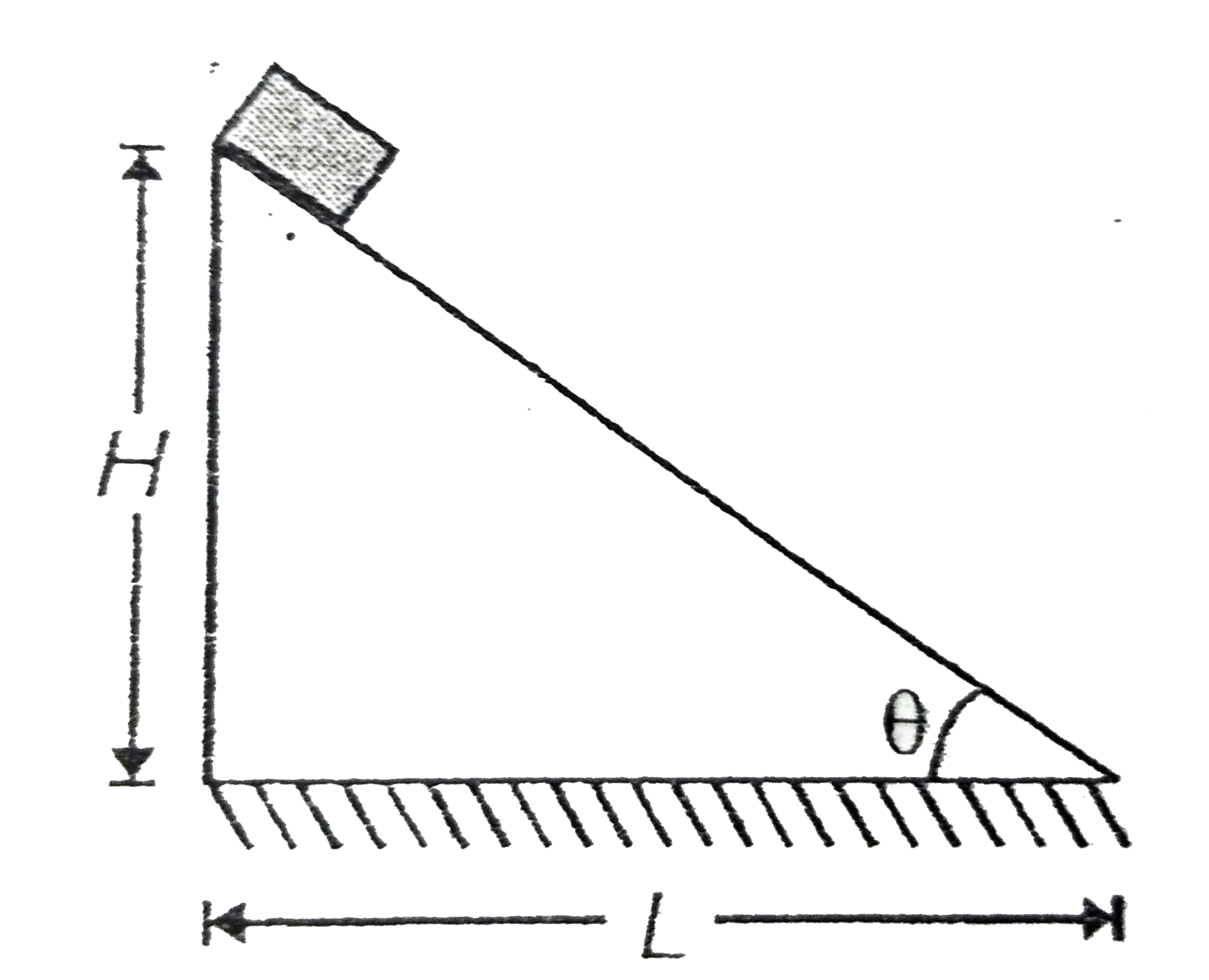
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View SolutionA block of 10 kg mass is placed on a rough inclined surface as shown in figure. The acceleration of the block will be
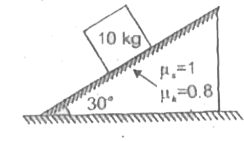
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View Solution
